【做题】POJ3469 Dual Core CPU——第一道网络流

刚学了Dinic就开始做题，然后就崩了。

题意：若干个任务，可以放在两个CPU中任意一个上完成，各有一定代价。其中又有若干对任务，如果它们不在同一个CPU上完成，会产生额外代价。最小化并输出代价。

一开始的想法是吧一个任务拆开成两个点（受2-sat的影响），然后就发现自己没法做了。首先，需要保证由同一个任务拆成的两个点只流过一个，这就会使最大流变成费用流。（我不会费用流）其次，难以满足第二个要求。后来一想，网络流与2-sat建图的区别在于网络流的状态表现在边的流量上（是否满流），而2-sat表现于同组点的取舍上。同样地，我也不能在2-sat和单位网络之间划等号。前者的作用是生成一个可行的方案，后者则是最优解。

那么，如上文所述，我们见图时要把状态表现在流量上。先不考虑额外代价，对于一个任务，它应该接着两条边表示两种选择。于是，可以从题解上抄到想到从超级源点向它建一条容量为第一种选择代价的边，从它向超级汇点建一条容量为第二种选择的边。此时这张图的最小割就是最优解。

然后考虑额外代价。存在这个代价当且仅当两个任务处割掉了位置不同的边。

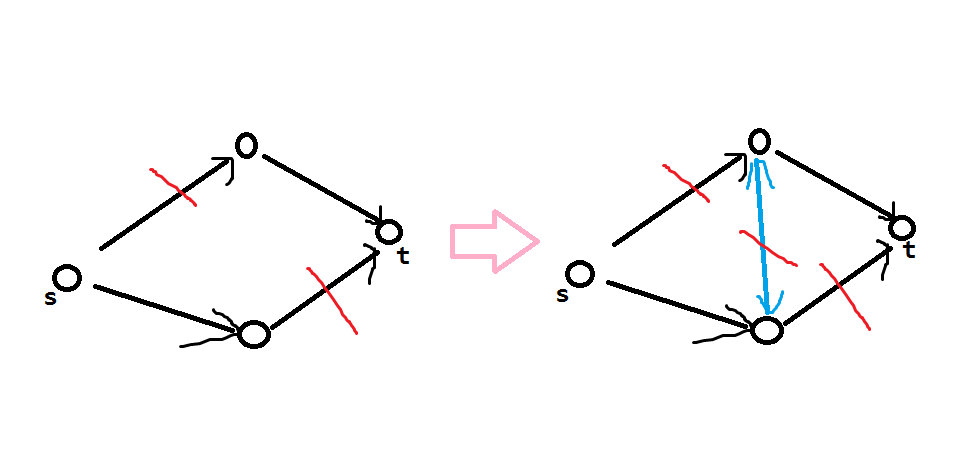
左上图：两个任务处割掉了位置不同的边

然后，我们只要在两个任务之间建一条容量为额外代价的双向边就可以了。这时因为割的性质就能把额外代价考虑其中了。并且，这不会影响其他情况。

故我们完成了建图，然后就只需要贴板子卡常就可以了。

令人震惊的是：时间复杂度O(n^2*m)。代码已自动过滤快读、register、inline

 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <queue>
 using namespace std;
 const int N = , M = , INF = <<;
 int n,m,s,t;
 struct edge {
     int la,b,cap,flo;
     edge(int la=,int b=,int cap=,int flo=):
         la(la),b(b),cap(cap),flo(flo){};
 }con[M<<];
 int tot,fir[N],cur[N],d[N];
 void add(int from,int to,int cap,int cap_back=) {
     con[++tot] = edge(fir[from],to,cap);
     fir[from] = tot;
     con[++tot] = edge(fir[to],from,cap_back);
     fir[to] = tot;
 }
 bool vis[N];
 void init() {
     for (int i=;i<=n;++i) cur[i] = fir[i];
     memset(vis,,sizeof vis);
 }
 bool bfs() {
     init();
     queue<int> q;
     while (!q.empty()) q.pop();
     q.push(s);
     d[s] = ;
     vis[s] = ;
     for (int pos = q.front();!q.empty();q.pop(),pos = q.front()) {
         for (int i=fir[pos];i;i=con[i].la) if (!vis[con[i].b]) {
             if (con[i].cap>con[i].flo) {
                 d[con[i].b] = d[pos] + ;
                 vis[con[i].b] = ;
                 q.push(con[i].b);
             }
         }
     }
     return vis[t];
 }
 int dfs(int x,int imp) {
     if (x == t||!imp) return imp;
     int expo = , tmp;
     for (int &i=cur[x];i;i=con[i].la) if (d[con[i].b] == d[x] + ) {
         tmp = dfs(con[i].b,min(imp,con[i].cap-con[i].flo));
         if (tmp > ) {
             con[i].flo += tmp;
             con[i^].flo -= tmp;
             expo += tmp;
             imp -= tmp;
             if (!imp) break;
         }
     }
     return expo;
 }
 int solve() {
     int res = ;
     while (bfs()) {
         res += dfs(s,INF);
     }
     return res;
 }
 int main() {
     int a,b,w;
     while (scanf("%d%d",&n,&m)!=EOF) {
         memset (fir,,sizeof fir);
         tot = ;
         for (int i=;i<=n;++i) {
             scanf("%d%d",&a,&b);
             add(n+,i,a);
             add(i,n+,b);
         }
         for (int i=;i<=m;++i) {
             scanf("%d%d",&a,&b,&w);
             add(a,b,w,w);
         }
         s = n+, t = n+;
         n += ;
         printf("%d\n",solve());
     }
     return ;
 }

小结：这可以说是对网络流模型的理解还不够。