如何选取一个神经网络中的超参数hyper-parameters

1.什么是超参数

所谓超参数，就是机器学习模型里面的框架参数。比如聚类方法里面类的个数，或者话题模型里面话题的个数等等，都称为超参数。它们跟训练过程中学习的参数（权重）是不一样的，通常是手工设定的，经过不断试错来调整，或者对一系列穷举出来的参数组合一通枚举（叫做网格搜索）。深度学习和神经网络模型，有很多这样的参数需要学习。

2.一些启发式规则

在实际应用中，当你使用神经网络去解决问题时，很难找到好的超参数。假设我们现在正在处理MINIST数据库的问题，并且对超参数是如何使用的一无所知。假设我们大部分超参数的选择如下：30 hidden neurons, a mini-batch size of 10, training for 30 epochs using the cross-entropy。但是学习速率和正则项系数的选择如下：learning rate η=10.0η=10.0 以及 regularization parameter λ=1000.0

我们的分类精度并不好。你可能会说“这很简单啊，减少学习速率和正则项系数”。但是你并不能先知这是由这两个超参数引起的问题。可能真实的原因是：“不管其它超参数如何选择，隐藏层包含30个神经元的网络就是性能不好”、“可能我们至少需要100个神经元或者300个”、或者“使用另一种方法来对输出进行编码”、“可能我们需要训练更多epochs”、“可能mini-batches太小了”、“可能我们需要另一种方法来初始化权值”等等。当你的网络很大、训练集很大时，这些超参数的问题可能会更让你抓狂。

接下来会介绍一些启发式规则，可以用来参考该如何设置超参数。当然这里所介绍的并不是全部的规则，总会有新的技巧可以用来提高你的网络性能。

2.1 广泛战略（Broad strategy）

我们使用神经网络来解决问题所面临的第一个挑战就是：我们希望网络有好的学习能力。也就是说，我们的网络所得到的结果肯定要比偶然结果好（要是连随随便便的一个网络的性能都比我们网络的好，那我们这个网络可见是有多差了）。但往往我们在面临一个新问题时，想要做到这点更是极其困难。下面有一些策略可以用于解决这个问题。

2.1.1 将问题拆分

假设你现在是第一次接触MINIST数据库，你就遭遇了上述问题：网络性能并不好。你要做的就是将问题拆开。将0s或1s的图像留下，丢掉其它所有的训练和验证图像，然后尝试着建立一个能将0和1分开的网络。这样做不仅比原先需要区分十种图像（数字0-9）要简单的多，而且减少了80%的训练数据量，将训练过程加速了5倍。

2.1.2 将网络拆分

为了进一步加速实验过程，你也可以将你的网络拆分为最简单的形式，只要这个形式可以进行有意义的学习。比如说，如果你觉得一个 [784, 10] 的网络对MINIST数字的分类结果better-than-chance，那你就可以从这样的一个网络开始训练，看看结果如何。这将会比直接训练一个 [784, 30, 10] 的网络要快的多。

2.1.3 提高监测频率

当超参数很多时，我们对性能的监测就会耗时很久。此时，我们可以通过更频繁地监测验证的准确度来更快地得到反馈，比如每训练1,000张图像之后就监测一次。此外，我们可以使用100张验证图像来更快地得到估计量，而不是全部的10,000张。关键就是提供大量的训练图像使得网络得到很好地训练，但只需粗略地估计性能即可。

这意味着你可以更快速地对超参数的其它choices进行测试，甚至可以几乎同时测试不同的choices。

接下来我们看一下具体的建议，我们将会讨论学习速率η、L2正则项系数λ，及小型批处理的大小（mini-batch size）。当然，这些建议也适用于其它超参数，包括那些与网络结构相关的参数、其它形式的正则项参数，以及往后将会见到的超参数——如动量系数（momentum co-efficient）等。

2.2 学习速率η

假设我们使用3个不同的学习速率来运行MINIST网络：η=0.025、η=0.25、η=2.5，其它参数像前面设置的一样，其中 λ=5.0，我们仍使用全部的50,000张训练图像。下图左是 training cost 的图表，可以看出：η=0.025时，cost下降的很平滑；η=0.25时，cost最开始处于下降状态，到epoch≈20时差不多就饱和了，再往后的改变很小且随机波动；η=2.5时，cost从一开始就波动很大。

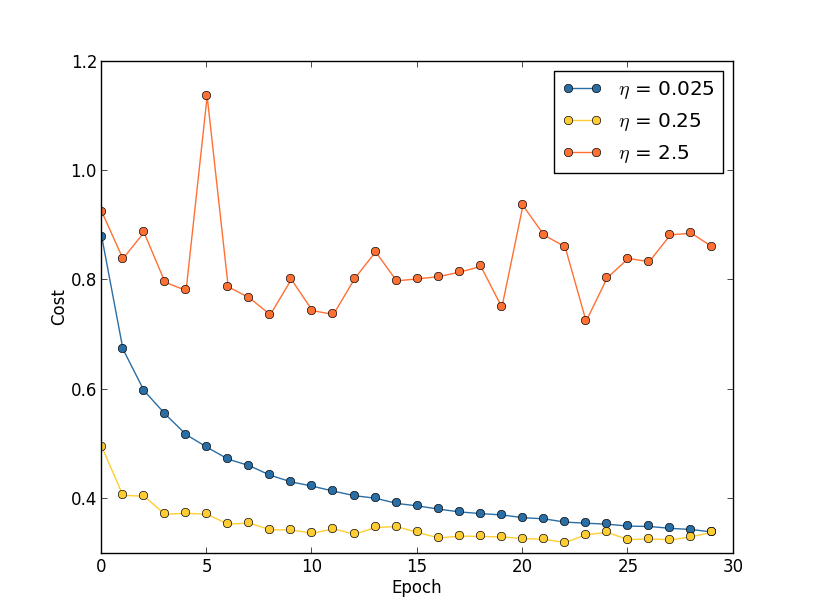
想要了解波动的原因，我们可以回想随机梯度下降法，它帮助我们逐渐滚落到损失函数的谷底，如上图右。所以，如果η过大，跨的一步也就越大，当快要到达谷底时，可能跨的一步就越过了谷底，也就是滚过了头。这也就是为什么当η=2.5时，cost曲线产生波动的原因。当η=0.25时，cost曲线的后面一部分也出现了同样的原因（overshooting problem）。而当η=0.025时，就没有出现这样的问题了。

虽然当η取的相对较小时，不会出现overshooting的问题，但是会出现另一个问题：减慢了随机梯度下降法。所以这个时候，一个更好的办法是：开始时，我们选取η=0.25，当epochs=20时，我们将 η 改为0.025。我们一会再讨论这个可变的学习率的问题，现在先弄明白如何找到一个固定的好的 η 值。

2.2.1 固定的学习率

首先，我们估计 η 的阈值。当 η 取这个阈值时，训练数据的cost立即开始减少，而不是产生波动或增加。这个估计不需要太过精确，你可以从 η=0.01 开始，然后依照量级开始增大。如果在前几个epochs中cost是减少的，你就可以依次尝试 η=0.1,1.0,……，直到某个 η 使得cost在前几个epochs中是波动的或增加的。如果从 η=0.01 开始，前几个epochs中cost是波动的或增加的，你就可以依次尝试η=0.001,0.0001,……，直到某个 η 使得cost在前几个epochs中是减少的。找到最大的 η 使得cost在前几个epochs中减少，比如 η=0.5 或 η=0.2（这个值不需要超级准确）。这样我们就得到了 η 的阈值。

显然，实际的 η 不应该大于这个阈值。事实上，如果 η 取这个阈值时，在许多epochs中仍然起作用，我们一般会将真正的 η 取的比这个阈值小，一般是阈值的1/2。这样的选择可以使你训练更多的epochs，而不会引起学习速率降低。

在MINIST数据这个例子中，在经过一些优化之后，我们得到的阈值为 η=0.5，按照上一段提到的规则，我们实际中选取的学习率 η=0.25。

这一切看似很简单，但是使用cost函数去选择 η 与我们前面所说的相矛盾了——我们会使用验证数据来评估性能，从而选取超参数。在实际中，我们会使用验证的精度去选择正则化系数、mini-batch的大小、网络参数（如层的数目和隐藏层神经元的个数等）等。

那为什么对学习率 η 的处理不同呢？坦白讲，这是我个人的审美偏好选择，也许是有些特殊。原因是：其它超参数是旨在提高测试集最终的分类精度，所以通过验证精度来选择它们毋庸置疑。但是，学习率只是偶然影响分类精度，它的主要目的是控制梯度下降中的步长（step）。所以说，监测训练的cost是检测step size是否太大的最好方法。

不过总的来说呢，这是个人偏好问题。如果验证精度提高，在学习的早期，训练cost一般只会减少。所以说，其实在实际应用中，不管你选哪种准则，影响都不大。

2.2.2 Early Stopping

Early Stopping的意思就是：在每一次epoch结束后，我们都计算一下在验证数据上的分类精度，当分类精度不再提高时，我们就终止训练。这使得epoch的值非常容易设置，这样我们就不用了解其它超参数是如何影响epoch的了。而且，Early Stopping也能自动防止网络过拟合。

不过呢，在实验的早期，关闭Early Stopping是需要的，这样你可以看到过拟合的任何signs，然后用它们去调整你的方法。

那么，分类精度不再提高是什么意思呢？因为分类精度在一次epoch中降低了，不是说就会一直下降了，可能在下一个epoch中又上升了，所以不能根据一两次的下降就说明分类精度“不再提高”了。正确的判断方法是：在训练的过程中，记录最佳的validation accuracy，当连续10次（或更多次）epoch都没达到最佳validation accuracy时，我们就可以认为是“不再提高”了。

此时，使用Early Stopping。这个策略就叫“no-improvement-in-n”，n即epoch的次数，可以根据实际情况取10、20、30……。因为有些网络可能在一段时间内（即n）进入了平稳期，在那之后accuracy可能又开始提高了。

（这个规则也可以不用于实验中）

2.2.3 可变的学习率

在前面我们讲了怎么寻找比较好的learning rate，方法就是不断尝试。在一开始的时候，我们可以将其设大一点，这样就可以使weights改变地比较快，从而让你看出cost曲线的走向（上升or下降）。进一步，你就可以决定增大还是减小learning rate。

但是问题是，找出这个合适的learning rate之后，我们前面的做法是在训练这个网络的整个过程中都使用这个learning rate，这显然不是好的方法。

在优化的过程中，learning rate应该是逐渐减小的，越接近“山谷”的时候，迈的“步伐”应该越小。

在讲前面那张cost曲线图时，我们说可以先将learning rate设置为0.25，到了第20个epoch时候设置为0.025。这是人工的调节，而且是在画出那张cost曲线图之后做出的决策。能不能让程序在训练过程中自动地决定在哪个时候减小learning rate？

答案是肯定的，而且做法很多。一个简单有效的做法就是：当validation accuracy满足 no-improvement-in-n规则时，本来我们是要early stopping的，但是我们可以不stop，而是让learning rate减半，之后让程序继续跑。下一次validation accuracy又满足no-improvement-in-n规则时，我们同样再将learning rate减半（此时就变为原始learning rate的四分之一了）…继续这个过程，直到learning rate变为原来的1/1024再终止程序。（1/1024还是1/512还是其他可以根据实际情况来确定）（也可以选择每次将learning rate除以10，而不是除以2）

2.3 正则项系数λ

正则项系数初始值应该设置为多少，好像也没有一个比较好的准则。

建议一开始将正则项系数λ设置为0.0，先用上述方法确定一个比较好的learning rate。然后固定该learning rate，给λ一个值（比如1.0），然后根据是否提高了validation accuracy，将λ增大或者减小10倍（增减10倍是粗调节，当你确定了λ的合适的数量级后，比如λ = 0.01,再进一步地细调节，比如调节为0.02，0.03，0.009之类。）

当正则项系数 λ 确定好之后，我们需要反过来再对learning rate进行优化。

2.4 Mini-batch size

首先说一下采用mini-batch时的权重更新规则。比如mini-batch size设为100，则权重更新的规则为：

也就是将100个样本的梯度求均值，替代online learning方法中求单个样本的梯度值：

当采用mini-batch时，我们可以将一个batch里的所有样本放在一个矩阵里，利用线性代数库来加速梯度的计算，这是工程实现中的一个优化方法。

那么，size要多大呢？一个大的batch，可以充分利用矩阵、线性代数库来进行计算的加速，batch越小，则加速效果可能越不明显。当然batch也不是越大越好，太大了，权重的更新就会不那么频繁，导致优化过程太漫长。所以mini-batch size选多少，不是一成不变的，根据你的数据集规模、你的设备计算能力去选。

幸运的是，使得学习速度最大的mini-batch size与其它超参数相对独立（除了整体结构），所以你不需要通过优化其它超参数，以便找到最佳的mini-batch size。所以，合适的做法是：首先为其它超参数选择一个合适的值（不一定是最优的），然后为mini-batch size尝试不同的值，像前面讲的那样缩放learning rate，最后画出实际运行时间（不是epoch）下的validation accuracy图像，然后观察哪个mini-batch size使得性能提高得最快。

得到了最优的mini-batch size，我们就可以对其它超参数进行优化了。

3.自动化技术

手动地优化是一个很好地理解神经网络如何工作的方法。然而，不出意外的是，有许多关于将这一过程自动化的研究。一个常见的技术是网格搜索（grid search），通过网格有系统地搜索超参数空间。

还有许多更复杂的方法，但要提到一篇用贝叶斯方法自动优化超参数的文章。

参考文献：

1. 什么是超参数
2. Michael A.Nielsen, “Neural Networks and Deep Learning“ Chapter3-how_to_choose_a_neural_network’s_hyper-parameters, Determination Press, 2015.
3. 这里也有他人关于第三章的中文理解——机器学习算法中如何选取超参数：学习速率、正则项系数、minibatch size
4. 选择可变学习速率的好处：Ciresan, Ueli Meier, Luca Maria Gambardella,”Deep Big Simple Neural Nets Excel on Handwritten Digit Recognition “
5. 关于神经网络中的一些技巧：Grégoire Montavon, Geneviève B. Orr, Klaus-Robert Müller, “Neural Networks：Tricks of the Trade” book
6. 关于网格搜索的成就和局限：James Bergstra, Yoshua Bengio, “Random search for hyper-parameter optimization”，2012 paper
7. 用贝叶斯自动优化超参数：Jasper Snoek, Hugo Larochelle, Ryan Adams, “Practical Bayesian optimization of machine learning algorithms”，2012 paper
8. 使用BP和梯度下降训练神经网络（包括深度神经网络）的一些实际建议：Yoshua Bengio, “Practical recommendations for gradient-based training of deep architectures”, 2012 paper
9. ：Yann LeCun, Léon Bottou, Genevieve Orr and Klaus-Robert Müller, “Efficient BackProp”, 1998 paper
10. 安逸轩博客： http://andyjin.applinzi.com/