【转载】 强化学习（二）马尔科夫决策过程(MDP)

原文地址：

https://www.cnblogs.com/pinard/p/9426283.html

---------------------------------------------------------------------------------------

在强化学习（一）模型基础中，我们讲到了强化学习模型的8个基本要素。但是仅凭这些要素还是无法使用强化学习来帮助我们解决问题的, 在讲到模型训练前，模型的简化也很重要，这一篇主要就是讲如何利用马尔科夫决策过程(Markov Decision Process，以下简称MDP)来简化强化学习的建模。

　　　　MDP这一篇对应Sutton书的第三章和UCL强化学习课程的第二讲。

1. 强化学习引入MDP的原因

对于马尔科夫性本身，我之前讲过的隐马尔科夫模型HMM（一）HMM模型，条件随机场CRF(一)从随机场到线性链条件随机场以及MCMC(二)马尔科夫链都有讲到。它本身是一个比较简单的假设，因此这里就不专门对“马尔可夫性”做专门的讲述了。

2. MDP的价值函数与贝尔曼方程

3. 状态价值函数与动作价值函数的递推关系

通俗说就是状态动作价值有两部分相加组成，第一部分是即时奖励，第二部分是环境所有可能出现的下一个状态的概率乘以该下一状态的状态价值，最后求和，并加上衰减。

　　　　这两个转化过程也可以从下图中直观的看出：

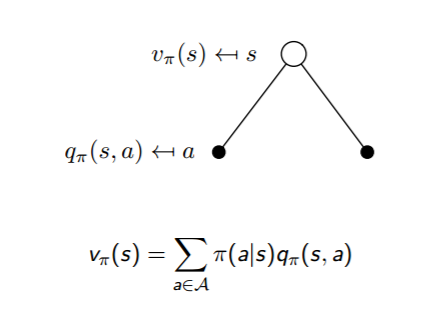
　　　　把上面两个式子互相结合起来，我们可以得到：

4. 最优价值函数

如何比较策略的优劣呢？一般是通过对应的价值函数来比较的，也就是说，寻找较优策略可以通过寻找较优的价值函数来完成。可以定义最优状态价值函数是所有策略下产生的众多状态价值函数中的最大者，即：

同理也可以定义最优动作价值函数是所有策略下产生的众多动作状态价值函数中的最大者，即：

对于最优的策略，基于动作价值函数我们可以定义为：

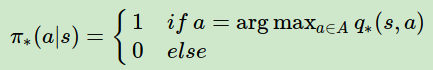
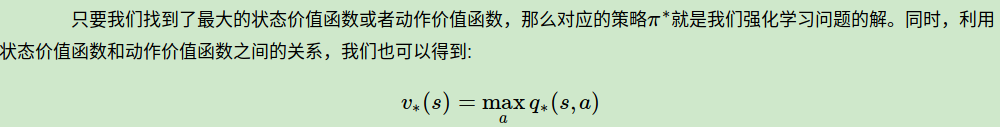
反过来的最优价值函数关系也很容易得到：

利用上面的两个式子也可以得到和第三节末尾类似的式子：

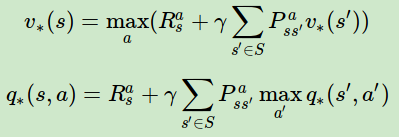
5. MDP实例

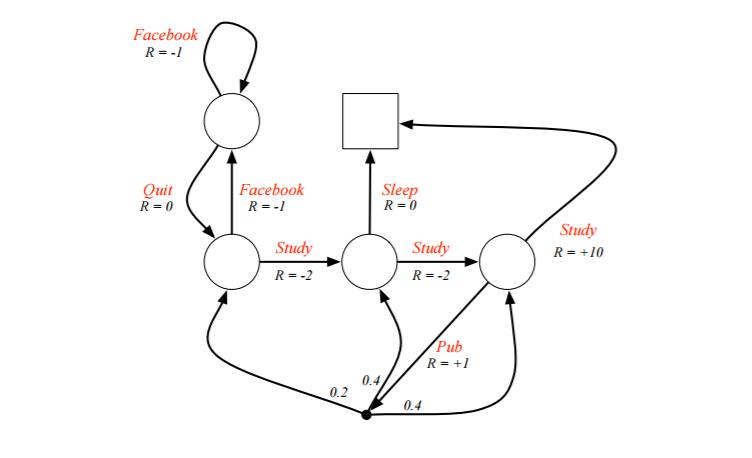
例子是一个学生学习考试的MDP。里面左下那个圆圈位置是起点，方框那个位置是终点。上面的动作有study, pub, facebook, quit, sleep，每个状态动作对应的即时奖励R已经标出来了。我们的目标是找到最优的动作价值函数或者状态价值函数，进而找出最优的策略。

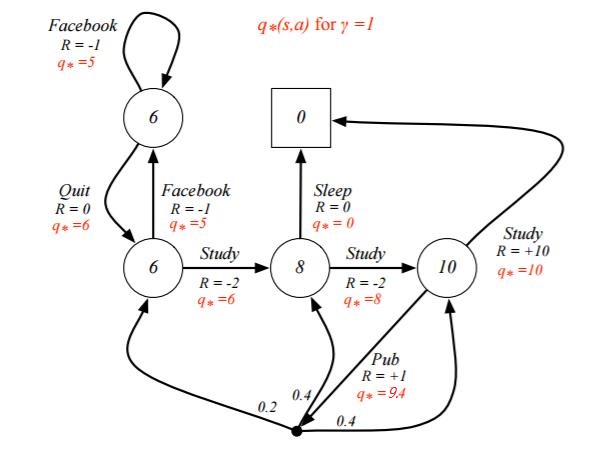
　　　　从而我们的最优决策路径是走6->6->8->10->结束。　　　　

6. MDP小结

　　　　MDP是强化学习入门的关键一步，如果这部分研究的比较清楚，后面的学习就会容易很多。因此值得多些时间在这里。虽然MDP可以直接用方程组来直接求解简单的问题，但是更复杂的问题却没有办法求解，因此我们还需要寻找其他有效的求解强化学习的方法。

　　　　下一篇讨论用动态规划的方法来求解强化学习的问题。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）

------------------------------------------------------------------------------------------------------------