二叉树的基础题目学习（EPI）

1.判断是个二叉树是不是平衡二叉树。

二叉树的定义都是利用递归的方法，所以二叉树有着天然的递归属性。所以一般情况下，递归解决二叉树问题中，递归解法比较简洁。平衡二叉树的定义是左子树和右子树均是平衡二叉树，并且左子树和右子树的高度差不超过1，三个条件缺一不可。

根据递归的定义，递归实现起来需要返回子树的高度，又要返回子树是否平衡的属性，所以判断平衡二叉树的递归算法需要传会两个参数，所以把递归函数原型定义为int balancedTree(TreeNode* root, bool &isBalanced)形式，返回值返回高度，其中引用形参也当做返回值代表子树是否平衡，这样实现起来比较容易了。（二叉树中好多算法递归均需要这种返回多个变量的递归写法，可以练习一下。举印象深刻的两个类似的：a.二叉树中最大路径（路径定义从任意一节点至任意另一节点），b.最近公共祖先问题，有更多的欢迎补充）。

一种开阔视野的方法：一种将空间复杂度近一步降低的方法是采用先序遍历，然后利用一个全局变量实时的记录stack的最大深度。《计算机编程艺术》第三卷，排序和查找460页证明了n个节点的平衡树的高度不会超过h_n=1.4405lg（n/2+3）-0.3277。如果遍历的时候栈的高度超过了这个高度，则这颗树为不平衡的树。

2.首先，设定一个概念，如果一棵树的左子树的节点数量和右子树的节点数量的差的绝对值不大于k，则该节点不是k平衡的。

题目：给定一个二叉树，找出二叉树中一个不是k平衡的节点，且此节点的后继节点均是k平衡的节点。

递归的查找即可，设定一个全局节点变量，初始化为NULL，递归中寻找到节点之后赋值给全局节点变量，递归函数中如果全局变量不为NULL，直接返回。递归函数返回值为当前树的节点数量即可。当前树的节点的数量=左子树节点数量+右子树节点数量+1，递归结束条件为节点未NULL，返回节点数量0。唯一赋值全局节点变量的地方就是第一次出现左子树与右子树差值绝对值超过k的时候，这时候沿着递归路径一路返回，全局变量及为所求。

3.判断二叉树是不是镜像的。

leetcode中存在原题，比较容易，同样利用递归判断，不过起始条件为左子树节点和右子树节点。递归函数isSymmetric（TreeNode *left, TreeNode *right），首先根节点必须相等，其次必须满足继续递归isSymmetric(left->right,right->let)&&isSymmetric(left->left,right->right)，三个条件同时满足，则才能够判断是镜像树。递归代码很简洁。

4.实现一个二叉树加锁的机制，限制条件是如果一个节点的后继节点或者祖先节点已经被锁定，则该节点不能够被锁定。实现isLock()，lock()，和unlock()操作，时间复杂度分别限制为O(1),O(h),O(h),其中h为树的高度。假设此二叉树存在指向父节点的指针。

每个节点添加一个标志位，简单实现O（1）的isLock()操作。

另外就是维护lock(),unlock()的时候维护节点的标志位操作了。加锁和解锁的时候需要考虑祖先，也需要考虑孩子，祖先可以在O（h）的时间复杂度内遍历获取状态。孩子节点如果逐个考虑可能需要O（n）了。所以不能逐个遍历，

这里可以在节点中继续保存一个变量，其为孩子节点是否被锁。该变量在lock的时候向上回溯祖先的时候逐个设置标志位即可。

所以解锁的时候进行相应的操作，解锁的时候需要释放其祖先节点中孩子加锁的标志，并且也需要更改是否锁定的标志。

5.给定一个存在父节点指针的二叉树表示，使用O（1）的额外空间遍历二叉树。（先序，中序，后序），不能修改树的结构。

Morris方法能够O（1）的空间复杂度实现二叉树的遍历，但是遍历过程中需要临时改变树形结构，所以该遍历算法不是线程安全的。

题目存在父节点指针，所以不需要利用栈来进行回溯，可以利用父节点指针回溯，所以可以达到O（1）的时间复杂度。

算法模板参考利用栈实现的后续遍历，设置当前节点指针cur，上一个节点指针pre。然后分三种情况讨论，

pre == NULL || pre->left == cur || pre->right == cur 这种属于traversal down的情况，继续向下遍历即可，临时利用next指针指向下一个节点

cur->left == pre 这种属于刚遍历完左子树，traversal up的情况

cur->right == pre 这种属于刚遍历完右子树，traversal up的情况

6.获得二叉树中序遍历的第k个节点的朴素方法遍历，统计到第k个节点输出即可，时间复杂度O（n）。假如给定的二叉树中每个节点包含其所有子树节点数量和，如何优化寻找第k个节点的算法。时间复杂度可以优化至O（h），h为树的高度。

其实题目思路比较容易获得，快速的缩减问题规模就可以了。查看当前节点的左子树的数量，

如果当前节点左子树的数量等于k，则可知当前节点为查找所需的节点。如果左子树的节点数量大于或等于k，则可以将问题缩小到寻找左子树的第k个节点。

如果当前节点左子树的数量小于k-1 ，则可知第k个节点在右子树中，寻找右子树中第k-（左子树节点数量+1）即可。

7.根据中序遍历和后序或者先序遍历还原二叉树。

leetcode中的题目，思路比较简单，后序/先序可以先确定根节点，根据根节点去分割中序遍历，递归调用左子树和右子树即可。

另外先序和后序无法唯一还原出二叉树，所以这种题目一般就是中序匹配另外一个遍历序。

扩展问题：根据给定的一个数组A，构造max树：max树定义是根节点为A数组中最大值，假设最大值的坐标为m，则左子树右A[0:m-1]构成，右子树由A[m+1,n]构成，递归的利用最大值构造左子树，右子树。设计高效的构造max树的方法。

比较直观的方法每次寻找最大值即可，这样每寻找最大值的时间复杂度为O（n），所以总的时间复杂度为O（n^2）。如果想要优化必须考虑从最大值获取的角度优化。可以分别从左至右，从右至左保存最大值。或者利用单调队列借助栈的功能完成预处理。

8.如果给定一个包含NULL节点的先序遍历结果，能够O（n）还原出二叉树吗？后序和中序呢？

这里借助栈即可，先序和后序，不断的从栈中弹出两个节点与当前节点构成小树压入栈。最后为一个完整的二叉树。

中序的遍历无法唯一还原出二叉树。因为所有树形的遍历结果序列均相同。

可以思考下包含NULL的层序遍历二叉树（也很简单）。

9.将二叉树的所有子节点连接成链表。

递归，然后判断是否子节点，如果子节点连接一下。保存一个全局的头结点变量即可。

10.设计一个输出二叉树外围节点的方法。外围节点的解释：下图需要输出的序列A,B,D,G,J,K,L,M,N,I,F,C

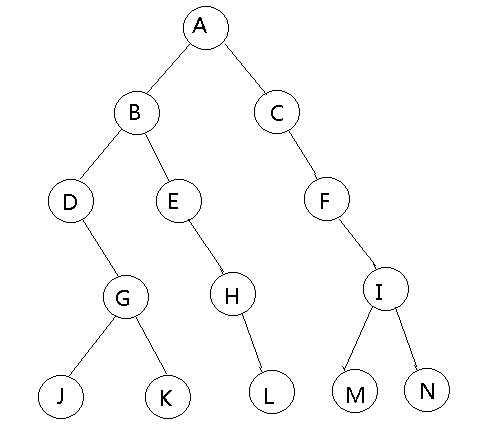
前一个题目已经完成了叶子节点的链表化了，输出也不是困难的事情，所以这个题目的难点在于输出左边外围和右边外围。

刚开始思考能否利用Morris遍历输出外围节点，后来画一个非完全二叉树之后发现挺复杂的。

答案的思路非常的简洁，左边外围节点的特点是如果当前节点外围节点，则该节点的左节点为外围节点，若左节点为空，则该节点的右子节点为外围节点。

右边外围节点的特点是如果当前节点外围节点，则该节点的右节点为外围节点，若右节点为空，则该节点的左子节点为外围节点。

注意，左边外围和右边外围节点的输出顺序，不同。右边可参考逆序输出链表，递归实现相当简洁。

11.求二叉树中两个节点最近公共组先的方法。

思路比较类似第一个题目的思路，递归，但是需要传递两个参数（或者最近公共祖先利用全局变量）

a.如果两个节点均在左子树，则递归左子树寻找最近公共祖先。

b.如果两个节点分别在左右子树，则当前节点返回。

c.如果当前节点为其中一个节点，则返回当前节点。

（这个算法从来没有coding过，需要练习一下，算是基础的操作）

12.如果二叉树中包含parent指针，可以优化二叉树中求两个节点最近公共祖先的方法吗？

有了parent指针，这样就可以同时从给定的两个节点向上找最先交叉的节点的，所以问题转换为两个单链表找最先出现交叉的节点。

a.方法是三遍扫描，首先针对每个节点，从当前节点统计至末尾节点，分别统计出两个链表的长度，然后长度较大的先走动长度之差的距离，然后两个指针同时走动，第一次汇合的地方就是最近的公共祖先。

b.如果使用上述的方法，时间复杂度为最深节点的深度。因为需要统计长度。然后后来该问题继续深入问了一下能够进一步优化时间复杂度。

当时想想确实没有办法进一步优化时间复杂度了，思路被阻塞了。完全没想到空间换时间的策略，题目没要求空间复杂度，就考虑一下牺牲空间。

策略是利用hash表，每次遍历两个节点，然后添加至hash表。同时向前推进，如果遍历的节点已经出现在hash表，表示该节点是第一次汇合的节点。（空间换取时间）

13.给定一个字符串S和一系列字符串集合D，找到S中最短的字符串前缀，满足该前缀不是D集合中任意一个字符串的前缀。

求最短公共前缀的方法是用Trie树，这里也需要使用Trie树的方法。（针对字符串，trie树的效率高于hash，fb的面试失败就是没有第一时间想到这个概念，用的不熟练）

Trie树字母表示在边的扩展中，节点一般存储true或者false代表是否到达单词，或者存储vector<string>容器代表该路径可达的所有单词，依据题目来决定Trie树的结构。

（需要练习一下）