ML（附录1）——梯度下降

　　梯度下降是迭代法的一种，可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。

　　简单地说，梯度下降就是沿着沿梯度下降的方向求解极小值时的自变量。

　　关于梯度的知识可参考《多变量微积分5——梯度与方向导数》

梯度下降的原理

　　二元函数w(x,y) = (x – 10)² + (y – 10)²，其梯度：

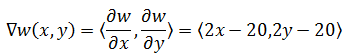
　　如果在w上选取一点(x_n, y_n)，w沿着梯度下降方向，在x方向上的变化率：

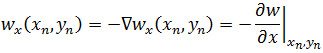
　　自变量x沿着梯度下降方向的变化：

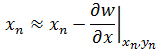
　　反复迭代，在达到临界点时，就可求得w在极小值时的x；同理可求得在极小值时的y。

　　问题是这样做实在太慢，迭代过程及其耗时，所以人们在此基础上设计出更加快速的处理办法——舍弃精确值，求得可接受的近似值。

学习率

　　实际应用中，梯度下降法增加了“学习率”的概念：

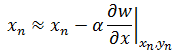
　　上式中的α就是学习率，也称为“步长”。梯度下降算法每次迭代，都会受到学习速率α的影响。偏导指明了变化的方向，而学习率则指明变化的步伐，实际上每次迭代一下，就可以更换一个新的α，只是为了方便才用一个。

　　本节剩余内容摘自 https://blog.csdn.net/chenguolinblog/article/details/52138510

　　如果α较小，则达到收敛所需要迭代的次数就会非常高；如果α较大，则每次迭代可能不会减小代价函数的结果，甚至会超过局部最小值导致无法收敛。如下图所示情况：

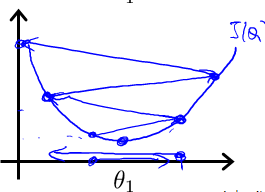
　　根据经验，可以从以下几个数值开始试验α的值，0.001 ,0.003, 0.01, 0.03, 0.1, 0.3, 1, …

　　α初始值位0.001, 不符合预期乘以3倍用0.003代替，不符合预期再用0.01替代，如此循环直至找到最合适的α，然后对于这些不同的 α 值，绘制 J(θ)随迭代步数变化的曲线，然后选择看上去使得 J(θ)快速下降的一个α值。观察下图，可以发现这2种情况下代价函数 J(θ)的迭代都不是正确的：

　　根据经验，可以从以下几个数值开始试验α的值，0.001 ,0.003, 0.01, 0.03, 0.1, 0.3, 1, …

　　α初始值位0.001, 不符合预期乘以3倍用0.003代替，不符合预期再用0.01替代，如此循环直至找到最合适的α，然后对于这些不同的 α 值，绘制 J(θ)随迭代步数变化的曲线，然后选择看上去使得 J(θ)快速下降的一个α值。观察下图，可以发现这2种情况下代价函数 J(θ)的迭代都不是正确的：

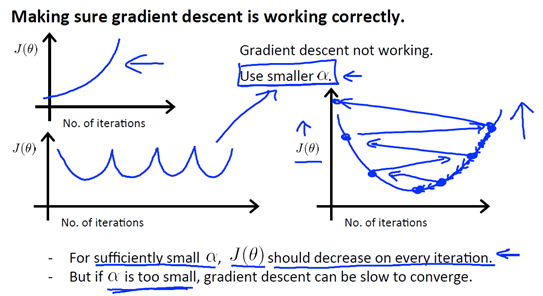
　　第一幅图，曲线在上升，明显J(θ)的值变得越来越大，说明应该选择较小的α

　　第二幅图，J(θ)的曲线，先下降，然后上升，接着又下降，然后又上升，如此往复。通常解决这个问题，还是选取较小的α。

在机器学习中的应用

　　如果机器学习算法的假设函数(hypothesis function) h_θ(x)如下：

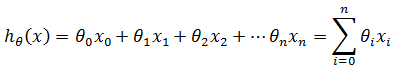
　　h_θ(x) 是线性回归模型，设x₀= 1，θ是权重，每个训练样本有n个特征，即训练样本是n维数据。对于初始权重，可全部设为一个常数。

　　对于给定的训练集，目标是找到最佳的h_θ(x)以拟合最多数据，此时损失函数J(θ)，也就是机器学习策略函数达到最小。如果全部预测正确，则对于所有训练数据都有h_θ(x) – y =0

　　如果用平方和定义J(θ)，则：

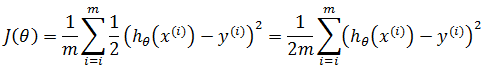
　　上式表示共有m训练样本，y表示实际结果，上标表示第i个训练样本，h_θ(x^（i）) - y⁽ⁱ⁾ 表示在训练集的第i个样本中，预测结果与实际结果的差值。前面加上1/2是为了在求导时使J(θ)简化，在后续推导中可以看到。

　　假设m = 1,即仅有一个训练样本，此时：

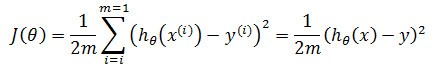
　　目标是使J(θ)达到最小，由于x和y已知，此时的 θ 值即为所求参数，根据梯度下降法：

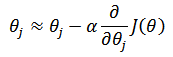
　　当i = 1时，第一个权重：

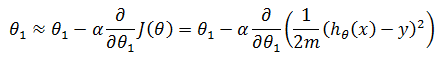
　　根据链式求导法则计算偏导（可参考《多变量微积分》的相关章节）：

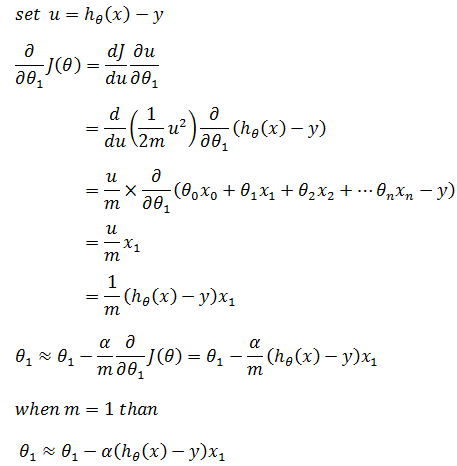
　　推广至m个训练样本，对于任意θ，梯度下降迭代表达式为：

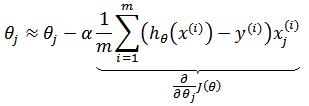
　　如果令θ是n维向量，可将上式化简：

　　如果用矩阵表示，梯度下降可以更加简洁：

　　当梯度下降到一定数值后，每次迭代的变化很小，这时可以设定一个阈值，只要变化小于该阈值，就停止迭代，而得到的结果也近似于最优解。需要注意的是，在新一轮迭代时，因为θ已经得到了更新，所以将使用新的h_θ

　　以二元特征为例，下面是正确做法和错误做法的对比：

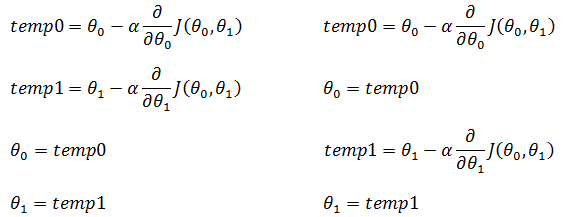
批量梯度下降法

　　上面对于权重的推导过程就是批量梯度下降法，每一次迭代都要遍历所有训练样本，不适用于训练样本数量极多的情况，于是提出了随机梯度下降。

　　优点：全局最优解；易于并行实现；

　　缺点：当样本数目很多时，训练过程会很慢。

随机梯度下降法

　　随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是每次仅仅选取第 i 个随机样本来求梯度：

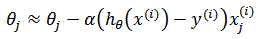
　　i 不是定值，在每次迭代时都重新选取。随机梯度下降法速度比批量梯度下降快了很多。随机梯度下降的每次迭代，有可能变大或变小，但总体趋势接近全局最优解，通常参数值会十分接近最小值。

　　优点：训练速度快；

　　缺点：准确度下降，并不是全局最优；不易于并行实现。

小批量梯度下降法

　　小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于m个样本，我们采用其中的k个来迭代，1<k<m。一般可以取x=10，当然根据样本的数据，可以调整k的值：

　　优点：两种算法的折中；

　　缺点：两种算法的折中。

　　如果样本量比较小，采用批量梯度下降算法。如果样本太大，或者在线算法，使用随机梯度下降算法。在一般情况下，采用小批量梯度下降算法。

与最小二乘法的比较

　　梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。最小二乘法可参考《多变量微积分笔记2——最小二乘法》。

---

作者：我是8位的

出处：http://www.cnblogs.com/bigmonkey

本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！

扫描二维码关注公众号“我是8位的”