SAT算法

今早用微云打的笔记...头大

我惊，这不是可爱的离散吗？！

建个有向图G，(Xi+Yi)加两边表示( ¬Xi+Yi)(Xi+ ¬Yi)

每个点（eg:A）加上 ¬A

下图为:(A->B)·( ¬B-> ¬A)·( ¬D->E)·( ¬E->D)·( ¬B->C)·( ¬C-> B)·(C-> ¬B)·(B-> ¬C)·(C->D)·(D->C)·(C-> ¬D)·( ¬D-> ¬C)

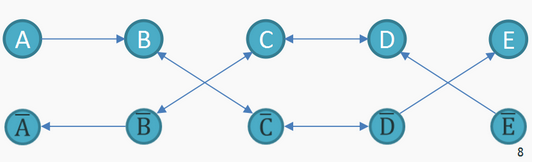
然后用Tarjan算法缩点

手热来了一发模板题https://www.luogu.org/problem/P4782

贴

 #include <bits/stdc++.h>
 using namespace std;
 const int N=1e6+;
 int n,m,a,b,fla,flb,cnt,head[N<<];
 int dfn[N<<],low[N<<],vis[N<<],col[N<<],scnt,idx;
 stack<int> st;
 struct edge{
     int to,next;
 }e[N<<];
 inline void addedge(int a,int b)
 {
     e[++cnt]={b,head[a]};
     head[a]=cnt;
 }
 void tarjan(int u)
 {
     dfn[u]=low[u]=++idx;vis[u]=;
     st.push(u);
     for(int i=head[u];i;i=e[i].next)
     {
         if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]);
         else if(vis[e[i].to]) low[u]=min(low[u],dfn[e[i].to]);
     }
     if(low[u]==dfn[u])
     {
         scnt++;int v=-;
         while(v!=u)
         {
             v=st.top();st.pop();
             col[v]=scnt,vis[v]=;
         }
     }
 }
 int main()
 {
     for(scanf("%d%d",&n,&m);m--;){
         scanf("%d%d%d%d",&a,&fla,&b,&flb);
         int aa=fla^,bb=flb^;
         addedge(a+aa*n,b+flb*n);
         addedge(b+bb*n,a+fla*n);
     }
     for(int i=;i<=*n;i++)
         if(!dfn[i]) tarjan(i);
     for(int i=;i<=n;i++)
         if(col[i]==col[n+i]) return puts("IMPOSSIBLE")&;
     puts("POSSIBLE");
     for(int i=;i<=n;i++) printf("%d%c",col[i]>col[n+i],i==n?'\n':' ');
 }

然后又很智障得磕了http://acm.hdu.edu.cn/showproblem.php?pid=3062

因为初始化和下标问题还WA了半天，就简单YES、NO的我都能PE，自闭半小时

贴

 #include <bits/stdc++.h>
 using namespace std;
 const int N=;
 int n,m,a,b,fla,flb,cnt,scnt,idx,flag;
 int head[N<<],dfn[N<<],low[N<<],vis[N<<],col[N<<];
 stack<int> st;
 struct edge{
     int to,next;
 }e[N*N];
 void init()
 {
     memset(head,-,sizeof(head));
     memset(dfn,,sizeof(dfn));
     memset(vis,,sizeof(vis));
     memset(low,,sizeof(low));
     cnt=idx=scnt=flag=;
 }
 inline void addedge(int a,int b)
 {
     e[cnt]={b,head[a]};
     head[a]=cnt++;
 }
 void tarjan(int u)
 {
     dfn[u]=low[u]=++idx;vis[u]=;
     st.push(u);
     for(int i=head[u];i!=-;i=e[i].next)
     {
         if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]);
         else if(vis[e[i].to]) low[u]=min(low[u],dfn[e[i].to]);
     }
     if(low[u]==dfn[u])
     {
         scnt++;
         int v=-;
         while(v!=u)
         {
             v=st.top();st.pop();
             col[v]=scnt,vis[v]=;
         }
     }
 }
 int main()
 {
     while(~scanf("%d",&n))
     {
         scanf("%d",&m);
         init();
         while(m--)
         {
             scanf("%d%d%d%d",&a,&b,&fla,&flb);
             addedge((a<<)+fla,((b<<)+flb)^);
             addedge((b<<)+flb,((a<<)+fla)^);
         }
         for(int i=;i<*n;i++)
             if(!dfn[i]) tarjan(i);
         for(int i=;i<*n;i+=)
             if(col[i]==col[i^]){puts("NO");flag=;break;}
         if(!flag) puts("YES");
     }
 }