bzoj1036 树的统计 树链剖分模板

题意：给出树上任意两点，求路径上的值的和与最大值，带单点修改操作

树链剖分思路：

1、对树进行dfs求出点的深度和父亲节点，然后求出轻重儿子（重儿子就是点最多的那个子树，其余都是轻儿子），用一个son数组指向每个节点的重儿子

2、对树进行第二次dfs，对于所有的重儿子，求出他的top节点也就是每个重儿子沿着重链可以到达的最远的那个祖先，然后维护dfs序，记录每个节点的访问次序以及第几次访问的是哪个节点，轻儿子的top节点就是本身

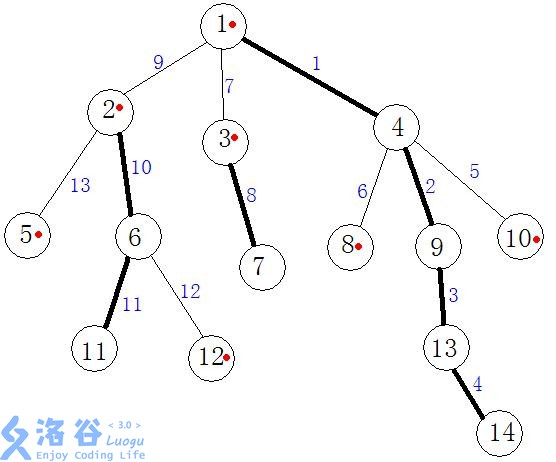
然后我们得到

dfs序：       1 4 9 13 14 8 10 3 7 2 6 11 12 5

top数组： 1 1 1 1 1  8 10 3 3 2 2 2 12 5（对应dfs序）

这样我们就把这棵树拆成了一条条的链（top值相同则为一条链上的点），用线段树维护这个dfs序，就可以快速求出链上最大值和值的和了，

对于任意两点，我们只需依次求出路径上的所有链的答案然后合并即可，可以证明路径上轻重链的条数是不超过logn的，这样单次查询的复杂度为O((logn)^2)

总时间复杂度O(q(logn)^2)

在计算两点答案的时候，采取一个巧妙的方法。首先若两个点不在同一条链上，我们总是让深度更大的那个点x往上跳到top[x]，并统计这条链的答案，直到两个点到同一条链上，最后计算在一条链上时的答案即可

AC代码(模板)

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+;
struct Edge
{
    int v,next;
}edge[N<<];
int sum[N<<],mx[N<<],n;
int head[N],tot,dep[N],fa[N],sz[N],son[N],top[N],id[N],rk[N],cnt,val[N];
void init()
{
    memset(head,-, sizeof(head));
    tot=;
}
void add(int u,int v)
{
    edge[tot].v=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void dfs1(int u,int f)
{
    dep[u]=dep[f]+;
    fa[u]=f;
    sz[u]=;
    for(int i=head[u];~i;i=edge[i].next)
    {
        int v=edge[i].v;
        if(v==f)continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(sz[v]>sz[son[u]])son[u]=v;
    }
}
void dfs2(int u,int t)
{
    top[u]=t;
    id[u]=++cnt;
    rk[cnt]=u;
    if(!son[u])return;
    dfs2(son[u],t);
    for(int i=head[u];~i;i=edge[i].next)
    {
        int v=edge[i].v;
        if(v!=son[u]&&v!=fa[u])dfs2(v,v);
    }
}
void pushup(int rt)
{
    sum[rt]=sum[rt<<]+sum[rt<<|];
    mx[rt]=max(mx[rt<<],mx[rt<<|]);
}
void build(int l,int r,int rt)
{
    if(l==r)
    {
        mx[rt]=sum[rt]=val[rk[l]];
        return;
    }
    int m=(l+r)>>;
    build(l,m,rt<<);
    build(m+,r,rt<<|);
    pushup(rt);
}
int querySum(int L,int R,int l,int r,int rt)
{
    if(L<=l&&r<=R)return sum[rt];
    int m=(l+r)>>;
    int res=;
    if(L<=m)res+=querySum(L,R,l,m,rt<<);
    if(R>m)res+=querySum(L,R,m+,r,rt<<|);
    return res;
}
int queryMax(int L,int R,int l,int r,int rt)
{
    if(L<=l&&r<=R)return mx[rt];
    int m=(l+r)>>;
    int res=-1e9;
    if(L<=m)res=max(res,queryMax(L,R,l,m,rt<<));
    if(R>m)res=max(res,queryMax(L,R,m+,r,rt<<|));
    return res;
}
void update(int pos,int val,int l,int r,int rt)
{
    if(l==r){
        sum[rt]=mx[rt]=val;
        return;
    }
    int m=(l+r)>>;
    if(pos<=m)update(pos,val,l,m,rt<<);
    else update(pos,val,m+,r,rt<<|);
    pushup(rt);
}
int getSum(int x,int y)
{
    int ans=;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        ans+=querySum(id[top[x]],id[x],,n,);
        x=fa[top[x]];
    }
    if(id[x]>id[y])swap(x,y);
    ans+=querySum(id[x],id[y],,n,);
    return ans;
}
int getMax(int x,int y)
{
    int ans=-1e9;
    while (top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        ans=max(ans,queryMax(id[top[x]],id[x],,n,));
        x=fa[top[x]];
    }
    if(id[x]>id[y])swap(x,y);
    ans=max(ans,queryMax(id[x],id[y],,n,));
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    init();
    int u,v;
    cin>>n;
    for(int i=;i<=n-;i++)
    {
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    for(int i=;i<=n;i++)cin>>val[i];
    dfs1(,);
    dfs2(,);
    build(,n,);
    int q,x,y;
    string op;
    cin>>q;
    while(q--)
    {
        cin>>op>>x>>y;
        if(op=="QMAX")cout<<getMax(x,y)<<'\n';
        else if(op=="QSUM")cout<<getSum(x,y)<<'\n';
        else update(id[x],y,,n,);
    }
    return ;
}