损失函数 - Andrew Ng机器学习公开课笔记1.2
线性回归中提到最小二乘损失函数及其相关知识。对于这一部分知识不清楚的同学能够參考上一篇文章《线性回归、梯度下降》。
本篇文章主要解说使用最小二乘法法构建损失函数和最小化损失函数的方法。
最小二乘法构建损失函数
最小二乘法也一种优化方法,用于求得目标函数的最优值。简单的说就是:让我们的预測值与真实值总的拟合误差(即总残差)达到最小。
在线性回归中使用最小二乘法构建了损失函数:
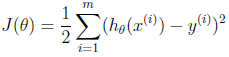
上一篇文章《线性回归、梯度下降》中提到求解使损失函数J(θ)取最小的θ值有两种方法:梯度下降(gradient descent)和正则方程(The normal equations)。以下主要讲一下正则方程。梯度下降方法最小化损失函数參考文章《线性回归、梯度下降》
正则方程
将训练特征表示为X矩阵,结果表示成y向量,仍然是线性回归模型。损失函数不变。那么θ能够直接由以下公式得出:

推导过程涉及线性代数方面的知识,这里不再具体展开线性代数知识。
设m为训练样本数;x为样本中的自变量,即二手房价格预測中的房屋面积和我是数目。x为n维向量;向量y为训练数据中的房屋价格。y为m维向量。那么训练数据能够用矩阵表示为:

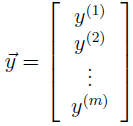
由于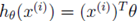 ,所以
,所以 就能够表示为:
就能够表示为:

损失函数就转化为:
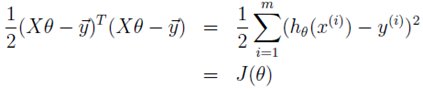
线性代数中有两个公式:
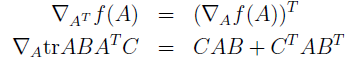
当中符号 表示一个m*n的矩阵。这个矩阵的第(i,j)个元素为
表示一个m*n的矩阵。这个矩阵的第(i,j)个元素为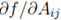 。
。
上面两个公式合起来能够表示为:

根据这这个公式对损失函数J(θ)推导:

为了最小化J(θ)。又由于J(θ)由最小二乘法得到,J(θ)的取值大于等于0。即最小值为0。
所以,我们使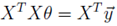 ,从而得到θ取值:
,从而得到θ取值:
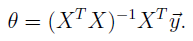
损失函数 - Andrew Ng机器学习公开课笔记1.2的更多相关文章
- Andrew Ng机器学习公开课笔记 -- 支持向量机
网易公开课,第6,7,8课 notes,http://cs229.stanford.edu/notes/cs229-notes3.pdf SVM-支持向量机算法概述, 这篇讲的挺好,可以参考 先继 ...
- Andrew Ng机器学习公开课笔记–Principal Components Analysis (PCA)
网易公开课,第14, 15课 notes,10 之前谈到的factor analysis,用EM算法找到潜在的因子变量,以达到降维的目的 这里介绍的是另外一种降维的方法,Principal Compo ...
- Andrew Ng机器学习公开课笔记 -- 学习理论
网易公开课,第9,10课 notes,http://cs229.stanford.edu/notes/cs229-notes4.pdf 这章要讨论的问题是,如何去评价和选择学习算法 Bias/va ...
- Andrew Ng机器学习公开课笔记 -- Regularization and Model Selection
网易公开课,第10,11课 notes,http://cs229.stanford.edu/notes/cs229-notes5.pdf Model Selection 首先需要解决的问题是,模型 ...
- Andrew Ng机器学习公开课笔记–Reinforcement Learning and Control
网易公开课,第16课 notes,12 前面的supervised learning,对于一个指定的x可以明确告诉你,正确的y是什么 但某些sequential decision making问题,比 ...
- Andrew Ng机器学习公开课笔记 – Factor Analysis
网易公开课,第13,14课 notes,9 本质上因子分析是一种降维算法 参考,http://www.douban.com/note/225942377/,浅谈主成分分析和因子分析 把大量的原始变量, ...
- Andrew Ng机器学习公开课笔记 -- 线性回归和梯度下降
网易公开课,监督学习应用.梯度下降 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 线性回归(Linear Regression) 先看个 ...
- Andrew Ng机器学习公开课笔记 -- Logistic Regression
网易公开课,第3,4课 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 前面讨论了线性回归问题, 符合高斯分布,使用最小二乘来作为损失函数 ...
- Andrew Ng机器学习公开课笔记–Independent Components Analysis
网易公开课,第15课 notes,11 参考, PCA本质是旋转找到新的基(basis),即坐标轴,并且新的基的维数大大降低 ICA也是找到新的基,但是目的是完全不一样的,而且ICA是不会降维的 对于 ...
随机推荐
- 配置Xcode版本控制SVN详细步骤内含解决Xcode/Mac OS10.8无法配置SVN的解决方法
本站文章均为李华明Himi原创,转载务必在明显处注明:(作者新浪微博:@李华明Himi ) 转载自[黑米GameDev街区] 原文链接: http://www.himigame.com/game-de ...
- 淘宝在hbase中的应用和优化
本文来自于NoSQLFan联合作者@koven2049,他在淘宝从事Hadoop及HBase相关的应用和优化. 对Hadoop.HBase都有深入的了解,本文就是其在工作中对HBase的应用优化小结, ...
- jquery源码10-提交的数据和ajax()
{ var r20 = /%20/g, //全部空格 rbracket = /\[\]$/, //结尾位置匹配中括号 rCRLF = /\r?\n/g, rsubmitterTypes = /^(?: ...
- kafka自带没web ui界面,怎么办?安装个第三方的
见 基于Web的Kafka管理器工具之Kafka-manager的编译部署详细安装 (支持kafka0.8.0.9和0.10以后版本)(图文详解)(默认端口或任意自定义端口)
- 将BT下载对抗到底
将BT下载对抗到底 随着互联网业务的多元化,各种P2P应用也越来越多,在企业中多数流量都会被类似于BT的下载所占用,BT之所以会危害到局域网,是因为它占用了大量网络带宽.网络管理员可以通过一 ...
- groupdel---删除指定的工作组
groupdel命令 groupdel命令用于删除指定的工作组,本命令要修改的系统文件包括/ect/group和/ect/gshadow.若该群组中仍包括某些用户,则必须先删除这些用户后,方能删除群组 ...
- matplotlib散点图笔记
定义: 由一组不连续的点完成的图形 散点图: 包含正相关性,负相关性和不相关性. 散点图生成函数: plt.scatter(x,y) 演示代码如下: import numpy as np import ...
- c、c++ 结构体的嵌套
c.c++ 结构体的嵌套 /************************************************************************/ /* 嵌套结构体 * C ...
- TrueSec引导的Linux系统和安全检测工具预览
650) this.width=650;" onclick='window.open("http://blog.51cto.com/viewpic.php?refimg=&qu ...
- Maven学习笔记5
Web项目的部署: web部署 配置步骤 生成项目方式不是quickstart,而是webapp. 默认目录结构,需要修改配置. 重新配置project facets和java compiler.并重 ...
