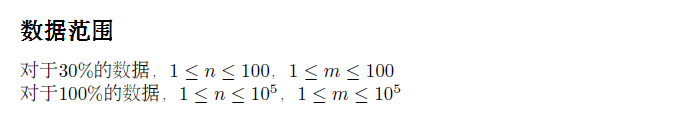[HEOI 2016] sort
[HEOI 2016] sort
解题报告
码线段树快调废我了= =
其实这题貌似暴力分很足,直接$STL$的$SORT$就能$80$
正解:
我们可以二分答案来做这道题
假设我们二分的答案为$a$,我们就可以将整个序列分为两个集合,一个是大于等于$a$的,一个是小于$a$的
那么我们就可以将大于等于$a$的赋值为$1$,小于$a$的赋值为$0$,那么对于排序,我们就变成了线段树区间覆盖,升序就将区间中所有的$0$覆盖到前面,$1$覆盖到后面,反之亦然。
最后我们查询询问位置的数,是$1$说明二分的答案小了,需要左边界右移,反之则右边界左移。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
inline int read(){
int sum();
char ch(getchar());
for(;ch<''||ch>'';ch=getchar());
for(;ch>=''&&ch<='';sum=sum*+(ch^),ch=getchar());
return sum;
}
int n,m,q;
int op[],l[],r[];
int a[];
int sum[],add[];
inline void pushup(int i){
sum[i]=sum[i<<]+sum[i<<|];
}
inline void pushdown(int i,int len){
if(add[i]!=-){
add[i<<]=add[i];
add[i<<|]=add[i];
sum[i<<]=add[i]*(len-(len>>));
sum[i<<|]=add[i]*(len>>);
add[i]=-;
}
}
inline void build(int l,int r,int i,int x){
add[i]=-;
if(l==r){
if(a[l]>=x)
sum[i]=;
else
sum[i]=;
return;
}
int mid((l+r)>>);
build(l,mid,i<<,x);
build(mid+,r,i<<|,x);
pushup(i);
}
inline void update(int ll,int rr,int l,int r,int w,int i){//cout<<"update"<<ll<<' '<<rr<<' '<<l<<' '<<r<<' '<<w<<' '<<i<<endl;
if(ll>rr)
return;
if(ll<=l&&r<=rr){
sum[i]=w*(r-l+);
add[i]=w;
return;
}
pushdown(i,r-l+);
int mid((l+r)>>);
if(ll<=mid)
update(ll,rr,l,mid,w,i<<);
if(mid<rr)
update(ll,rr,mid+,r,w,i<<|);
pushup(i);
}
inline int query(int ll,int rr,int l,int r,int i){
if(ll<=l&&r<=rr)
return sum[i];
pushdown(i,r-l+);
int mid((l+r)>>),ret();
if(ll<=mid)
ret+=query(ll,rr,l,mid,i<<);
if(mid<rr)
ret+=query(ll,rr,mid+,r,i<<|);
return ret;
}
inline bool check(int x){
build(,n,,x);
for(int i=;i<=m;++i){//cout<<l[i]<<' '<<r[i]<<endl;
int tmp(query(l[i],r[i],,n,));//cout<<i<<' '<<op[i]<<' '<<l[i]<<' '<<r[i]<<endl;
if(op[i]==){//cout<<r[i]-tmp+1<<' '<<r[i]<<"devide"<<l[i]<<' '<<r[i]-tmp<<endl;
update(l[i],r[i]-tmp,,n,,);
if(tmp!=)
update(r[i]-tmp+,r[i],,n,,);
}
else{//cout<<l[i]<<' '<<l[i]+tmp-1<<"devide"<<l[i]+tmp<<' '<<r[i]<<endl;
update(l[i],l[i]+tmp-,,n,,);
if(tmp!=r[i]-l[i]+)
update(l[i]+tmp,r[i],,n,,);
}
}
return query(q,q,,n,);
}
inline void ef(int l,int r){
while(l+<r){
int mid((l+r)>>);
if(check(mid))
l=mid;
else
r=mid;
}
printf("%d",l);
}
inline int gg(){
freopen("heoi2016_sort.in","r",stdin);
freopen("heoi2016_sort.out","w",stdout);
n=read(),m=read();
for(int i=;i<=n;++i)
a[i]=read();
for(int i=;i<=m;++i)
op[i]=read(),l[i]=read(),r[i]=read();
q=read();
ef(,n);
// printf("%d",ans);
return ;
}
int K(gg());
int main(){;}
[HEOI 2016] sort的更多相关文章
- HEOI 2016 游记
闲来无事,把这玩意儿补上. OI生涯中第一次正经的考试.挂的很惨. Day -1 不小心把机油(雾)sm惹毛了. 好像没啥别的事儿. Day 0 说好了上午直接去机房,然而临时说让我们上完前两节课再去 ...
- [TJOI 2016&HEOI 2016]排序
Description 在2016年,佳媛姐姐喜欢上了数字序列.因而他经常研究关于序列的一些奇奇怪怪的问题,现在他在研究一个难题 ,需要你来帮助他.这个难题是这样子的:给出一个1到n的全排列,现在对这 ...
- [HEOI 2016] seq
题解: 发现多决策且明显无后效性,果断dp,那么转移方程F[i]=F[j]+1 设R[I]为改变之后的最大值,L[i]为改变之后的最小值 由于只能改变一个元素 所以转移的条件是 (j<i &am ...
- 数据结构(并查集||树链剖分):HEOI 2016 tree
[注意事项] 为了体现增强版,题目限制和数据范围有所增强: 时间限制:1.5s 内存限制:128MB 对于15% 的数据,1<=N,Q<=1000. 对于35% 的数据,1<=N,Q ...
- 字符串[未AC](后缀自动机):HEOI 2016 str
超级恶心,先后用set维护right,再用主席树维护,全部超时,本地测是AC的.放心,BZOJ上还是1S限制,貌似只有常数优化到一定境界的人才能AC吧. 总之我是精神胜利了哦耶QAQ #include ...
- [TJOI 2016&HEOI 2016]求和
Description 题库链接 求 \[f(n)=\sum_{i=0}^n\sum_{j=0}^i S(i,j)\times 2^j \times (j!)\] \(S(i, j)\) 表示第二类斯 ...
- 解题:HEOI 2016 求和
题面 我们需要知道这样一个东西(大概叫 斯特林公式?) $S(i,j)=\frac{1}{j!}\sum\limits_{k=0}^{j}(-1)^k C_j^k(j-k)^i$ 那么就是推啊 $=\ ...
- [ HEOI 2016 ] 树
\(\\\) Description 给出一颗树,开始只有 \(1\) 号节点有标记. \(\ C\ x\) 对 \(x\) 号节点打标记 \(\ Q\ x\) 查询 \(x\) 号节点深度最深的有标 ...
- COGS 2274. [HEOI 2016] tree
★☆ 输入文件:heoi2016_tree.in 输出文件:heoi2016_tree.out 简单对比时间限制:1 s 内存限制:128 MB 这道题数据弱到炸了 . 第一次做用树刨 ...
随机推荐
- P1491 集合位置 次短路
这个题是一个次短路的裸题,就是把最短路路径求出来之后依次删边,然后跑最短路,在这些情况里取最小值就行了. 题干: 每次有大的活动,大家都要在一起“聚一聚”,不管是去好乐迪,还是避风塘,或者汤姆熊,大家 ...
- B1826 [JSOI2010]缓存交换 贪心+离散化+堆
这个题仔细一想可以直接贪心做,因为队列里下一个出现的早的一定最优.正确性显然.然后我只拿了50,我直接模拟另一个队列暴力修改最后一个点的nxt值,自然会T.但是其实不用修改,直接插入就行了前面的不影响 ...
- Spark SQL 操作Hive 数据
Spark 2.0以前版本:val sparkConf = new SparkConf().setAppName("soyo") val spark = new SparkC ...
- Istio 1.1部署实践
前提条件 正确安装配置Kubernetes集群 CentOS Linux release 7.5.1804 安装 下载istio 1.1版本 [root@vm157 ~]# wget https:// ...
- Rails5 Controller Document
更新: 2017/06/28 大致完成全部 更新: 2017/06/29 补充module文件命名规则 更新: 2017/07/09 补充session的设置 更新: 2018/03/06 修正ren ...
- codevs1230元素查找(hash)
1230 元素查找 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description 给出n个正整数,然后有m个询问,每个询问一个 ...
- codevs1369 xth 砍树(线段树)
1369 xth 砍树 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description 在一个凉爽的夏夜,xth 和 rabbi ...
- Java中的自定义注解
## 元注解 要声明一个注解, 我们需要元注解, 元注解是指注解的注解,包括@Retention, @Target, @Document, @Inherited. @Retention 注解的保留位置 ...
- DropDownList 数据源绑定和获取
前台代码: <td>账户名称:</td> <td> <asp:DropDownList ID="DropDownListAccount" ...
- mysql触发器的操作
一.创建触发器 1.创建有一条执行语句的触发器 CREATE TRIGGER trigger_name BEFORE|AFTER trigger_EVENT(INSERT|DELETE|UPDATE) ...