2019年北航OO第一单元（表达式求导任务）总结

2019面向对象课设第一单元总结

一、三次作业总结

1. 第一次作业

1.1 需求分析

第一次作业的需求是完成简单多项式导函数的求解，表达式中每一项均为简单的常数乘以幂函数形式，优化目标为最短输出。为了满足优化目标，我们需要将含有相同指数的项进行合并。

1.2 实现方案

根据需求，我们很容易就能想到利用HashMap构建常数和幂指数的对应关系（再加上这是第一次作业，本以为只是让我们借此熟悉一下Java语法，于是并没有考虑程序可扩展性），于是仅建立了Polynomial多项式类和用作主函数的TestDerivative类（本人的风格一直是建立一个单独的main函数类，在其中保持尽可能小的代码规模，尽量10行以内解决问题），并利用Polynomial类中的属性HashMap<BigInteger, BigDecimal> terms（在第一次作业时我错误地认为还可以识别浮点数）进行表达式信息的存储。对于错误处理，由于错误输入的判断可能在程序中的多处出现，于是我设立了用于检测错误的IllegalInputException类作为程序中使用的输入异常类，在发现输入出错时将其抛出，并通过调用逐层向上传递至main函数进行统一的捕捉处理。程序UML图如下：

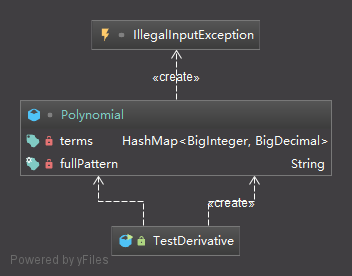
求导程序具体实现中的难点在于三处：输入串处理、求导以及表达式输出。

在本程序中对于输入串的处理仅仅利用了Polynomial类的parse()函数，首先利用正则表达式进行非法字符/非法空格的判断，接着删去所有空格进行整体表达式的合法性判断，再根据正负号进行切分，对切分出的每个项根据*号和^号分离出系数和指数填充HashMap。在填充时，对于HashMap中已有的项不能进行替换而是需要进行系数相加，于是还需要多一步判断。在求导时，对于HashMap的每一项遍历计算产生新项是非常简单的，最终返回一个新的Polynomial。输出时，由于当时并不知道toString()方法的重写，于是自己写了一个print()函数。

1.3 结构分析

此次作业中，解决关键问题的仅有Polynomial类中的parse()（一个函数解决输入处理）、calculate()（一个函数解决求导）、print()（一个函数解决输出）。

本次作业的度量如下：

指标	项目平均值	项目总值	特殊值
Lines of Code（总行数）	58	176
Lines of Code per Method（方法行数）	17.625		Polynomial.parse() - 60
Essential Cyclomatic Complexity（本质复杂度）	1.75		Polynomial.parse() - 5
Design Complexity（设计复杂度）	3.75		Polynomial.parse() - 13
Cyclomatic Complexity（循环复杂度）	5.25		Polynomial.parse() - 18，Polynomial.print() - 15
Average Operation Complexity（平均操作复杂度）	4.25		Polynomial - 5.33
Weighted Method Complexity（加权方法复杂度）	11.33	34	Polynomial - 32
Cyclic Dependencies（循环依赖）	0	0
Depth of Inheritance Tree（继承树深度）	0	0

本次作业不愧是我写的第一个正经OO程序（先前编译课设虽然用C++虽然也按功能分了不同类，有一点OO的苗头，但奈何所有字段都是public，住手这不是OO），一分析就发现充满了各种各样的问题，其中还有两个UA类都没写在表格里（一个是主类，一个是异常类，这个任务下异常类难道除了extends Exception之后调用super()方法以外还需要写别的么）。在这里面，Polynomial.parse()的问题极大，可以看出其惊人的60行顶格代码行数带来的是极大的复杂度，甚至连设计复杂度都很大，这意味着对于字符串的处理不仅应该分成若干个更小的函数，将判断字符串合法和分析字符串两项功能分开，同时自己在处理字符串时运用的算法也是开销极大的，有不小的优化空间。实际上此次在分析字符串时，我采用的不是正则表达式匹配，而是采用了字符遍历的方式，这种方式需要使用的的String类函数调用使得设计复杂度大幅度提升。对于Polynomial.print()函数，其复杂的优化逻辑同样让循环复杂度相当大，其中充斥着对HashMap的各种操作。反思一下，虽然在此次任务中利用StringBuilder将系数、x和指数进行字符串拼接是一种较为直接的想法，但是其复杂度却很高。由于本次只有一种对象，循环依赖和继承树深度均为0。

1.4 测试思路

此次作业相对简单，测试的思路也并不复杂，只需要按照指导书对每一种不同的省略输入进行测试即可。由于代码逻辑较为简单，Debug没有给我留下什么深刻印象，线上测试也没错，因此也省略下面的Bug分析部分。

2. 第二次作业

2.1 需求分析

第二次作业需要完成简单幂函数和简单正余弦函数求导。相比于第一次作业，增加了因子类别sin(x)和cos(x)，且因子之间可以相乘了。优化目标依然是最短输出，优化方案有二：合并同类项，利用cos(x)+sin(x)=1进行展开或合并。

2.2 实现方案

在第二次作业的实现中，受第一次作业“对应关系”思路的影响，我依然在寻求优化过程中存在的对应关系。对于项的合并，此次任务中没有了系数和指数的对应关系，然而，由于合并同类项的过程中不存在括号，能够合并的项仅有除系数外完全相同的项，因此在多项式中存储的应为项与系数的对应。对于因子的合并，需要对同类型因子进行合并，所以此处的对应关系为因子类型与指数的对应。因此，我建立了描述因子类型的枚举类FactorType用于存储四种类型因子的正则表达式并实现了查看匹配何种类型因子的方法（这么看来有种工厂模式的影子？）。对于因子类Factor，存储因子类别、系数和指数，为求导时产生带系数的项做准备；对于项类Term，存储因子类别与因子对应的HashMap；对于多项式类Polynomial， 建立项类别与项对应的HashMap。为此，需要在FactorType，Term两个类中重写equals()和hashCode()方法以识别同类型因子类型或项。程序UML图如下（复杂了不少呢）：

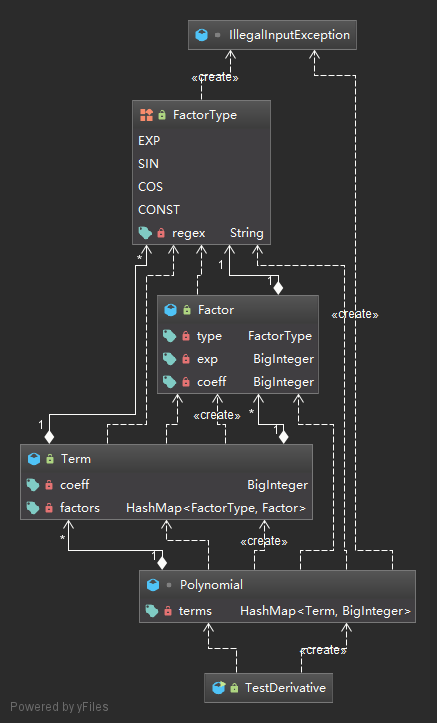
本次作业除了上次继承的三个主要问题外，还新增了优化问题。

对于输入处理，本次去掉了无用的间接处理方法，而是直接在构造器中进行分析，实现了高内聚。此外，由于表达式更加复杂，我转而使用表达式树的逐层正则判断方式：在Polynomial中，将输入串根据符合条件的+-号位置将表达式切分成一个个项字符串，将每个字符串交由Term处理；在Term中，将传入的输入串根据符合条件的*号位置将项切分成一个个因子字符串，将每个字符串交由Factor处理；在Factor中，调用工厂函数FactorType.parse()完成因子类型判断+系数/指数分析。由于此处的FactorType类为枚举类型，使得4种因子类型遍历更为方便，同时在后续作业因子更为复杂时可以直接将该类转为接口，以便后续作业添加更多因子类型，极大地增加了可扩展性。

对于求导处理，在不同的类中采用不同的求导策略：对于因子，在Factor类中分因子类型采取不同的求导策略，实现链式法则；在Term类中对因子遍历，利用双重循环每次保证只有外层循环遍历到的因子求导，其余因子保留，实现乘法法则；在Polynomial类中对项遍历，将结果相加，实现加法法则。

对于输出，由于表达式树的每一层均重写了属于该类的toString()方法，使得底层只需考虑最简单的单因子转换，而类/表达式仅需将底层传上来的字符串进行简单符号连接即可，这种分对象进行处理的方式免去了多种情况讨论的复杂逻辑，十分方便且耦合较为简单。

对于优化，我依然对于可合并的项和因子重写equals()和hashCode()方法判断是否可合并，从而最大限度地合并同类项/同类因子。对于sin(x)和cos(x)的合并问题，该问题是一个仅能寻求近似解的问题：由于可能涉及到项的拆分，所以该任务不能仅由简单的贪心完成；同时，拆分时能采取的公式并不止sin(x)+cos(x)=1一个，诸如平方和/立方和公式都可以使用，这大大增加了优化成本；论坛内的DFS+贪心策略虽然可以实现，但风险过大，由于性能分仅占20%，正确性依然是首先需要保证的，所以我仅仅实现了最简单的sin(x)^2+cos(x)2=1的合并。实现方法是对于每一次出现sin(x)^{2或是cos(x)}2，都计算其对偶项（也就是将cos(x)替换为sin(x)​，反之亦然）的项，并在表达式中进行查找。虽然低效，却也能实现最基本的功能，不过如此简单的合并在实际操作中很难遇到可以进行优化的情形。

2.3 结构分析

本次作业将三个主要任务下放至三个层次的类中分别处理该层的对应特征。本次作业的度量如下：

指标	项目平均值	项目总值	特殊值
Lines of Code（总行数）	104	627
Lines of Code per Method（方法行数）	11.731		Factor.calcFactorDiff() - 51
Essential Cyclomatic Complexity（本质复杂度）	1.67		Factor.toString() - 9, FactorType.parse() - 5
Design Complexity（设计复杂度）	3.09		Polynomial.toString() - 13, Factor.calcFactorDiff() - 11, Factor.toString() - 9, Term.getDualTerm() - 9
Cyclomatic Complexity（循环复杂度）	5.25		Polynomial.toString() - 15, Factor.calcFactorDiff() - 11
Average Operation Complexity（平均操作复杂度）	2.88		Polynomial - 4.44
Weighted Method Complexity（加权方法复杂度）	20.67	124	Polynomial - 40, Term - 40, Factor - 36
Cyclic Dependencies（循环依赖）	0	0
Depth of Inheritance Tree（继承树深度）	0	0

本次作业在将不同种对象在类中加以区分之后在各项指标的平均值上均出现了下降，这表明面向对象的思路的确可以通过将单一任务区分为不同类对象的分任务的方式降低程序复杂度，同时让编程思路更加清晰。但是，此次OO的思路依然没有贯穿始终，从因子求导方法Factor.calcFactorDiff()的高复杂度就能看出：多种因子实际上应该分为子类继承于Factor类之下，而非将所有类型的因子都归为一类并在方法中利用低效switch语句进行区分。Polynomial.toString()类依然继承了第一次作业的写法，复杂度依然居高不下。Term类由于加入了很多优化判断方法，故其WMC很高。

2.4 测试思路

本次测试需要生成大量表达式，而若是通过自己思考生成表达式则容易在构造样例时采用与代码同样的思路，从而绕开自己潜在的错误。为此，我利用Python脚本，运用Xeger包生成符合要求的表达式，并调用Mathematica进行fuzzing测试，通过与自己的结果进行比较来探求程序中的bug。

Mathematica的优点在于其能够快速生成表达式的导函数，并能够直接通过表达式进行等价判断。但是在引入三角函数后，其复杂的诱导公式使得较长的公式无法直接进行判断，这也直接导致了测试中的表达式串都相对偏短。但是在测试中，长度带来的限制是容易自己构造的，因此我在自动测试中简单地跳过了无法判断的式子。这在一定程度上增加了fuzzing失败的风险，但是不失为当时的一种可行方案。最终发现的bug较少，最终测试中也并没有问题，所以跳过bug部分。

2.5 总结反思

此次程序中有几个设计不到位的地方：首先是在Term中Expression中实现的对应关系不对称，这让身为强迫症的我写代码总有一种不舒服的感觉…归根到底，这种失败设计的根源在于没有意识到系数实际上是一种特殊的因子，这让我在处理系数时相当棘手。在今后的设计中，应该保持观察对象的敏锐性，进一步发现问题中每个元素的更高抽象层次。

其次，FactorType类的设计初衷是为了增加程序的可扩展性，以便在之后需求增加时能够快速反应。但是，可扩展性的弊端在于其弱化了程序的建模：在此次作业中总共有4种不同类型的因子，因此正如讨论区所说，每一个项均可以看做由一个5维向量存储的对象，这5个量分别代表了一个项的系数和四种因子的次数。由此，优化时可以不需要再通过Term深入两层获得其某些因子的信息，而是可以直接通过其向量进行优化。在设计类时，除了考虑其实际意义与可扩展性外，同样应该看到当下的限制对当下项目的特殊性：往往多加的限制是对当下项目简化建模结构，方便优化的必要条件。在可扩展性和建模的简化性上不应该像这次项目一样一味地偏向一方（实际上第三次作业依然对本次设计做了小重构，真是失败呢），而是需要做好两边的权衡。

3. 第三次作业

3.1 需求分析

第三次作业加入了表达式和sin/cos​因子嵌套。嵌套使得可以通过括号进行更大范围的同类项合并，同时表达式树深度也可以大幅增加。

3.2 实现方案

在该任务中，已经很难看到之前作业那种很明显的对应关系，因为因子和项已经可以嵌套，而且可以变得相当复杂。因此，我延续了第二次作业的表达式树结构，并将系数归于因子管理、系数作为一种特殊的因子归于项管理。同时，在此次作业中我实现了工厂类Factor，并在每一种类型的Factor中放入了符合该类型因子特征的正则表达式REGEX作为其属性，并标记public static final对Factor类开放，从而让工厂可以自动地通过逐一判断返回恰当的因子类型。在存储上，此次改用了HashSet以方便进行表达式/因子合并优化。程序UML图如下：

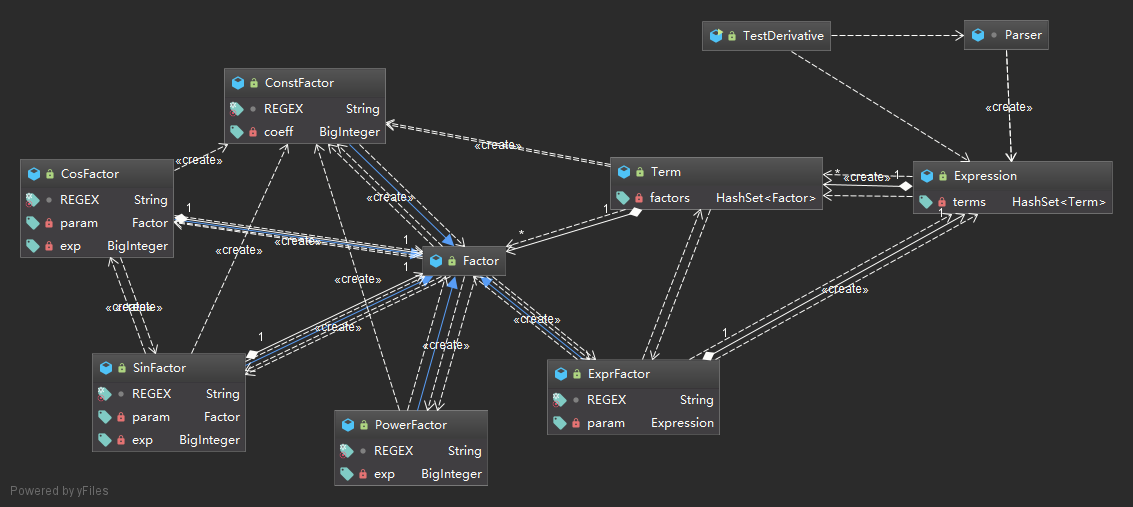
对于输入处理，依然延续了先前的在Expression中根据+-截断，在Term中根据*截断，并最终给Factor进行因子匹配的思路构建表达式树。与先前不同的地方在于，此次由于因子内依然可以包含表达式，所以需要在每一次截断时进行多一步匹配：必须使得截断的符号在最外层括号之外。此处，在分析开始前，我首先利用Parser类进行输入串的初步分析，包括是否为空/非法字符探测/非法空格探测等等。在删除掉所有空格后，首先遍历输入字符串，并利用栈（此处并不需要维护一个真正的Stack，而是可以利用一个初值为0的数int parenStack通过加1和减1操作模拟压栈和弹栈）维护当前字符处的括号情况，当栈为空（即当前符号不在任何一对括号内）且当前字符为需要截断的字符时，向其之前增加一个特殊字符作为标记，在遍历完成后根据该特殊字符进行截断进行下一层分析。对于表达式类ExprFactor中表达式的提取，只需要利用String.substring(1，str.length()-1)将外层的两个括号去掉，传给Expression类进行匹配即可。在任何一步中出现正则表达式无法匹配的情况，都会抛出一个IllegalInputException，由函数逐层穿给其调用函数，直至抛给main()进行错误输出。这样的匹配模式不需要一个统一的输入处理类，而是由各个类自己利用构造器根据输入字符串构造属于自己的对象，将任务进行了分派，更符合面向对象的思想。

对于求导处理，此次的实现更为清晰：所有可以求导的对象（包括Factor及其子类，Term和Expression）均实现求导接口Derivable，并在因子类中实现链式法则，在项类中实现乘法法则，在表达式类中实现加法法则。求导的结果最终会由表达式树的低端依次向上传递，直至传递到最高层的Expression中。

对于输出处理，同样分派给各个类去实现自己的toString()函数。这样可以将输出的优化尽可能分散开，便于查找错误。

对于优化，此次由于优化分数很少，所以并没有实现有关sin​/cos​的优化。然而，此次依然进行了合并同类项以及合并同类因子的操作：由于在表达式的每个层次中均采用HashSet进行存储，其目的是在每一个表达式中只存储不能合并的项以及在每个项中存储不能合并的因子，所以对equals()和hashCode()的重写需要使得能合并的项相等。但是，对于每个因子而言，其括号内部的表达式/项必须完全一致才能保证可合并，因此，需要实现一个表示对象完全相同的函数fullEquals()。这样，通过两个功能不同的equals()和fullEquals()即可轻松实现对HashSet中可合并项的查找及合并。

3.3 结构分析

本次作业的度量如下：

指标	项目平均值	项目总值	特殊值
Lines of Code（总行数）	69	1027
Lines of Code per Method（方法行数）	7.6
Essential Cyclomatic Complexity（本质复杂度）	1.71		Term.equals() - 7, CosFactor.CosFactor() - 7, SinFactor.SinFactor() - 7, Factor.parseFactor() - 6, Parser.parenMatchingCheck() - 6
Design Complexity（设计复杂度）	2.18		Expression.Expression() - 12, Term.toString() - 11
Cyclomatic Complexity（循环复杂度）	2.55		Expression.Expression() - 16, Term.toString() - 12
Average Operation Complexity（平均操作复杂度）	2.18		Term - 3.93, Parser - 3.67, Expression - 3.50
Weighted Method Complexity（加权方法复杂度）	17.64	194	Term - 55, Expression - 35
Cyclic Dependencies（循环依赖）		6
Depth of Inheritance Tree（继承树深度）	1.3	3

本次作业在各项复杂度指标上相比于上一次作业又有了大幅下降，这表明对于各个类的功能分拆取得了很大成效。而Expression构造器的复杂度较高可能是因为沿用了先前的处理方式吧（笑）。Term类作为联系表达式和因子的桥梁，其WMC值较高也是有一定道理的。在方法的本质复杂度上，所有经过了字符串遍历用栈来维护括号对应的方法复杂度都较高，因为其中出现了一些较复杂的判断，无法避免，而Expression构造器中依然不仅存在括号栈的问题，还需要根据其前2位是否为符号进一步判断调用Term的子串起始位置，所以出现了复杂度较高的情况。实际上，可以将这两部分分成两个方法。

3.4 测试思路

本次测试我利用了加强的Python脚本进行测试。Mathematica虽然功能强大，但是与Python的交互需要通过subprocess调用命令行完成，甚至必须经过读写文件的过程，系统开销巨大；与此同时，Mathematica的表达式等价性判断也局限了表达式复杂度。在此次fuzzing测试中，我同样利用Xeger包生成表达式，转而利用Anaconda原生的代数库Sympy进行测试。

在测试中，字符串的生成是一个挑战，由于在Java项目中利用单一正则表达式进行输入匹配已经相当具有挑战性，利用Xeger一次性生成所有可能表达式也很有难度。因此，我利用构造表达式树的反向思维，首先利用Xeger生成一些带临时标志的表达式/项/因子模板，再进行循环，对上一轮增添的临时标志用新生成的串进行替换。为了避免替换的串一直含有临时标志导致循环无法终止，我设定了max_round常数用于终止循环，当循环次数大于max_round时只能向其中填充幂函数项，由于幂函数项不存在因子/表达式参数，所以可以保证其生成的内容中不含有临时标志。对于每一次填充因子时，首先随机生成一个0~4之间的数，表示此次生成因子的类型，而后根据对应的因子正则表达式生成该类型因子进行临时标志替换。此次自动测试的表达式生成代码如下（其中临时标志的设置为：'@'表示应该填充项，'#'和'~'表示应该填充因子，'!'表示应该填充表达式）：

expressionRegex = "^(@[+-]{1,2})*@$"
termRegex = "^(#\\*)*#$"
sinFactorRegex = "^sin\\(~\\)(\\^(\\+)?[1-9]\\d{0,1})?$"
cosFactorRegex = "^cos\\(~\\)(\\^(\\+)?[1-9]\\d{0,1})?$"
powerFactorRegex = "^x(\\^(\\+)?[1-9]\\d{0,1})?$"
constFactorRegex = "^[+-]?(([1-9]\\d{0,1})|0)$"
exprFactorRegex = "^\\(!\\)$"
x = Xeger(limit=2)

def generate():
    max_round = 2
    result: str = x.xeger(expressionRegex)
    generate_round = 0
    while True:
        generate_round += 1
        for termCount in range(result.count('@')):
            result = result.replace('@', x.xeger(termRegex), 1)
        for factorCount in range(result.count('#')):
            factor_type = random.randint(0, 4)
            if factor_type == 0:
                if generate_round > max_round:
                    result = result.replace('#', x.xeger(powerFactorRegex), 1)
                else:
                    result = result.replace('#', x.xeger(sinFactorRegex), 1)
            elif factor_type == 1:
                if generate_round > max_round:
                    result = result.replace('#', x.xeger(powerFactorRegex), 1)
                else:
                    result = result.replace('#', x.xeger(cosFactorRegex), 1)
            elif factor_type == 2:
                result = result.replace('#', x.xeger(powerFactorRegex), 1)
            elif factor_type == 3:
                result = result.replace('#', x.xeger(constFactorRegex), 1)
            elif factor_type == 4:
                if generate_round > max_round:
                    result = result.replace('#', x.xeger(powerFactorRegex), 1)
                else:
                    result = result.replace('#', x.xeger(exprFactorRegex), 1)
        for innerCount in range(result.count('~')):
            factor_type = random.randint(0, 4)
            if factor_type == 0:
                if generate_round > max_round:
                    result = result.replace('~', x.xeger(powerFactorRegex), 1)
                else:
                    result = result.replace('~', x.xeger(sinFactorRegex), 1)
            elif factor_type == 1:
                if generate_round > max_round:
                    result = result.replace('~', x.xeger(powerFactorRegex), 1)
                else:
                    result = result.replace('~', x.xeger(cosFactorRegex), 1)
            elif factor_type == 2:
                result = result.replace('~', x.xeger(powerFactorRegex), 1)
            elif factor_type == 3:
                result.replace('~', x.xeger(constFactorRegex), 1)
            elif factor_type == 4:
                if generate_round > max_round:
                    result = result.replace('~', x.xeger(powerFactorRegex), 1)
                else:
                    result = result.replace('~', x.xeger(exprFactorRegex), 1)
        for exprCount in range(result.count('!')):
            result = result.replace('!', x.xeger(expressionRegex), 1)
        if result.find('@') == -1 and result.find('#') == -1 and result.find('~') == -1 and result.find('!') == -1:
            break
    return result

在生成目标字符串之后，我将20个数分别带入Sympy计算的导数以及Java程序计算的导数中，并比较二者差值与1e-6的大小来确定自己的程序是否出现错误。

利用该测试程序，我可以通过设置第8行的limit和第12行的max_round分别改变生成串的单个元素长度以及式子的嵌套深度。由于替换算法较为复杂，当两个参数超过3时生成表达式会异常缓慢，不过在两个参数分别为2、3和3、2时生成的表达式已经足够长，嵌套深度也较大；此外，通过修改正则表达式，还可以进行系数为0等针对性测试。利用该自动测试，我发现了不少两个equals()使用相反的bug。除了equals()和fullEquals()用反的bug外，对于对象引用的操作也是一个易错点，对此，最简单的解决方案就是在需要传对象应用的类实现Clonable接口并重写clone()方法。但是，这一偷懒的操作不得不说成为了之后我犯错的伏笔。

3.5 bug修复

在此次强测前，我利用自己的自动测试程序做了10000+次fuzzing测试，确保自己的程序正确性没有问题。然而，在本次的强测中，我被判了4个点的CPU_TIME_LIMIT_EXCEED，这是我绝对没有想到的。在这4个测试点中，均出现了表达式因子的大量括号嵌套，而在本地测试中，我仅通过5层括号嵌套确保了自己的正确性，却没有发现，当表达式因子的括号为7层时运行会出现0.5秒左右的卡顿，而括号大于10层时已经无法看到运行结果。在平时的测试中，我的自动测试程序曾生成过7层sin/cos嵌套的情况，可以瞬间输出答案，而这是因为因子中的参数是另一个因子；而表达式因子中，参数作为一个表达式，对其进行拆解需要经过表达式→项→因子三层，当括号嵌套过多时则会出现内存不够用的情况。对此，正确的修复应该是在每一次表达式因子ExprFactor调用Expression.Expression()构造器前，首先探寻最内层括号的位置，直接通过字符串操作将多余括号略去。

3.6 总结反思

此次作业真的是白 优 化 了，在准备时只考虑正确性却未曾考虑过超时/超内存的我被教了很关键的一课。但是从好的方面想，这次惨痛的教训让我了解到，在将来思考代码结构时，不能把内存看作是一种无限的资源，而是要尽可能在保证正确性的情况下减小内存占用，无论是否关乎正确性，在进行数据预处理时就将能节约内存/运行时间的优化率先做完，会让自己在之后的编码中少一些顾虑。此外，此次的内存爆炸很大程度上与我的自动测试程序给我的盲目自信相关：碰巧由于自动测试程序无法生成嵌套层数过多的表达式因子，这导致自己无法生成会导致内存错误的样例，这说明正确性测试/边界条件测试是不能替代压力测试的，极限情况不仅包含数据边界，更包含压力边界，前者决定了能否在任何时候输出的是正确结果，后者决定了能否在任何时候输出。

二、创造性模式应用

在本次作业中，虽然自己没有意识到，但是第三次作业中的Factor类实际上应用了工厂模式，通过实现parseFactor()方法，我对于每一个传入的项字符串都对各个种类因子分别进行了正则匹配以寻求正确的返回类型：

static Factor parseComplexFactor(String input)
            throws IllegalInputException {
        if (input.matches(SinFactor.REGEX)) {
            return new SinFactor(input);
        } else if (input.matches(CosFactor.REGEX)) {
            return new CosFactor(input);
        } else if (input.matches(PowerFactor.REGEX)) {
            return new PowerFactor(input);
        } else if (input.matches(ConstFactor.REGEX)) {
            return new ConstFactor(input);
        } else if (input.matches(ExprFactor.REGEX)) {
            return new ExprFactor(input);
        } else {
            throw new IllegalInputException();
        }
    }

由于本次作业中，各类因子的添加需要在同一个位置进行判断，它们又继承自同一个类，所以在本次作业中非常适合应用工厂模式。在实际应用中，我使用的是一个简单工厂，通过工厂类中提供的函数进行构造。但是，Factor类作为所有因子的父类，不应该再多实现一个工厂功能，而是应该单独建立工厂类进行操作；同时，这种朴素的实现方法等价于用switch-case对所有子类进行遍历，当子类类型增加时还需要对工厂类进行修改，不符合开闭原则。一个符合开闭原则的实现方式是利用反射机制，还有一种是不利用反射机制的类注册模式。这种模式在每一个子类中增加注册函数对工厂类传入该子类的注册信息，在工厂类中维护一个HashMap维护一个标签和类/实例的映射从而实现在工厂类中的便捷遍历，这种实现符合开闭原则，虽然稍显复杂但可扩展性得以增强。

三、特典金曲《没 BUG 人（TV Size）》

在总结的最后的最后，有感而发为大家献唱一曲《没 BUG 人》（雾，我自己还远远没有达到这个层次），与大家共勉~

噔蹬蹬↗ 蹬蹬 蹬 蹬（镜头放大到bug上）

あれは誰だ 誰だ 誰だ 那是谁 是谁 是谁

あれはNO BUG NO BUG MAN NO BUG MAN 那是没BUG 没BUG人 没BUG人

『没人能说自己没有BUG』の 名をうけて 背负着『没人能说自己没有BUG』的名义

すべてを捨てて たたかう男 舍弃了一切（指课余时间）去战斗的男人（？）

NO BUG MANアローは Object Oriented 没BUG人之箭是面向对象

NO BUG MANイアーは Programming Style 没BUG人之耳是风格规范

NO BUG MANウイングは JUnit 没BUG人之翼是单元测试

NO BUG MANビームは Python Script 没BUG人的光束是脚本强测

アーdalaoの力 身につけた 将dalao之力 集于一身

正義のヒーロー 正义的英雄

NO BUGマン NO BUGマン 没BUG人 没BUG人