想说再见不容易，win7最新市占率依然超36%

微软正在通过努力让Windows 7用户升级至Windows 10，不过从目前的市占率来看，他们还是要加把劲了。

微软正在通过努力让Windows 7用户升级至Windows 10，不过从目前的市占率来看，他们还是要加把劲了。

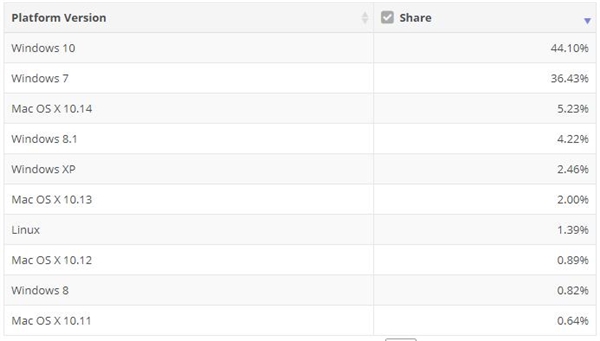
据最新的市场份额看，Windows 10在本月的市场份额有所提升，从43.62％增长到44.10％。另一方面，Windows 7仅略有下降，从36.52％下降至36.43％。

这种转变很可能成为微软的一项艰难的努力，许多用户预计会拒绝升级并且即使在支持结束后也坚持使用Windows 7，尽管随着接近2020年1月的最后期限，转换的用户数量会增加。

需要注意的是Win7主要支持已经在2015年1月13日终止了，不过外延支持是到2020年1月14日，所谓外延支持是不再有产品设计及功能更新，只有基本的安全补丁更新，当然客户要是花钱要求支持，微软还是会答应的，免费支持是没有了。

这并非微软最后一次通知，在Win7剩余的几个月中，微软会间歇性地提醒用户Win7“快死亡”的这个事实。