RS中的关系引用不明确以及行列自动添加了追溯
问题1:由于在FM模型的物理层是自己新建了查询主题,查询主题采用对已经存在的表进行sql处理然后重命名,
使用的是sql类型的数据源,sql类型设置的查询类型是默认的cognos类型,而语法是本地的结果出现下面的错误
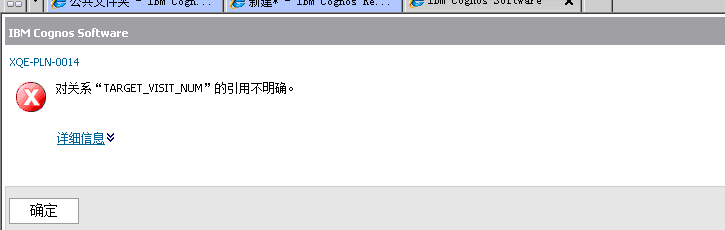
解决办法,进入FM模型设置-SQL设置-SQL类型设置为本地,保存模型重新发布就好了
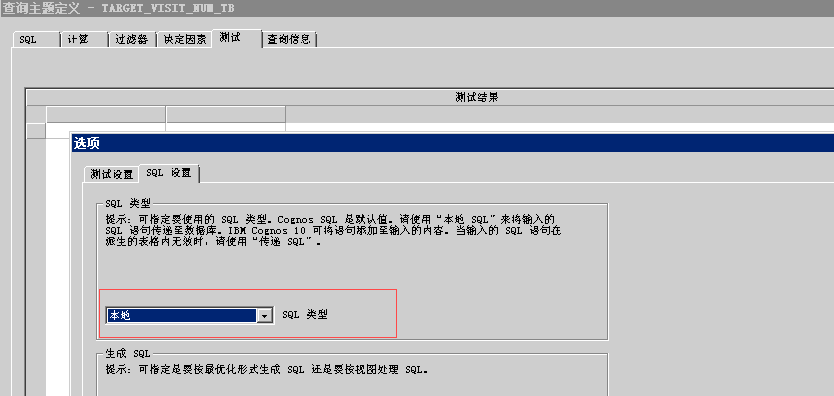
问题2:在报表设计的过程中,难免存在复制别的报表的操作,以提升开发效率,结果出现了下面的错误,模型原始的数据项都自动添加上了
下划线,而且鼠标停留还可以点击,点击了之后还可以追溯到本身,最底层就不变,如果有子对象,就跳转到子对象

于是就以为是之前的人设置了追溯,去页面找,半天没有在列和行对象上找到任何蛛丝马迹,于是重整思路,这应该是在整个页面或者布局上做了什么手脚,于是来到
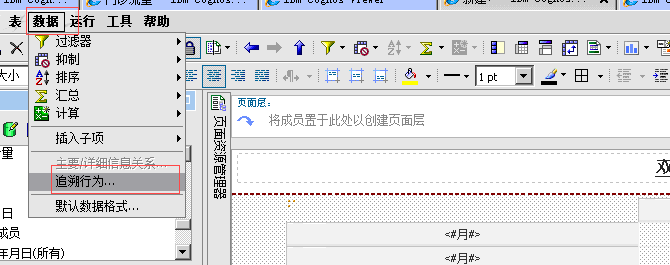
进入追溯行为,勾掉第一个允许向上追溯和向下追溯
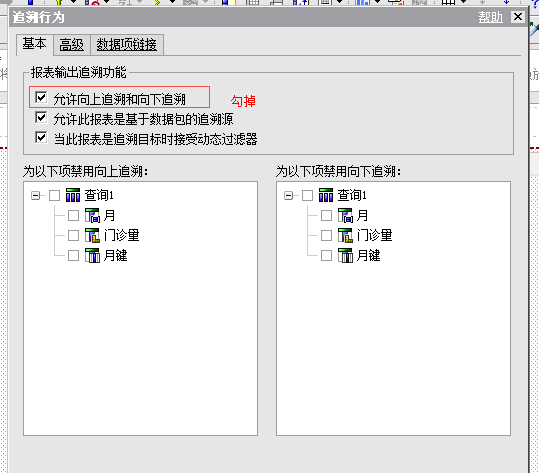
结果是

PS:‘允许向上追溯和向下追溯’在RS中,默认是不勾选的,除非你自己主动勾选,一般在多层次的上钻下钻中可以勾选
RS中的关系引用不明确以及行列自动添加了追溯的更多相关文章
- jmeter csv Data Set Config 文件中带引号的数据转换问题(自动添加双引号解决办法)
1.我们从csv中获取数据,在jmeter中使用这些数据,其中csv的数据如图,有的数据包含引号. 2.问题:我们获取的json数据,被自动添加了双引号 3.解决方式: 在CSV Data Set C ...
- 在编写wpf界面时候中出现如下错误: 类型引用不明确。至少有两个名称空间(“System.Windows”和“System.Windows”)中已出现名为“VisualStateManager”的类型。请考虑调整程序集 XmlnsDefinition 特性。
wpf中类型引用不明确.至少有两个名称空间(“System.Windows”和“System.Windows”)中已出现名为“VisualState 你是不是用了WPFToolKit?如果是的,那原因 ...
- C++ 中指针与引用的区别
指向不同类型的指针的区别在于指针类型可以知道编译器解释某个特定地址(指针指向的地址)中的内存内容及大小,而void*指针则只表示一个内存地址,编译器不能通过该指针所指向对象的类型和大小,因此想要通过v ...
- 1.【使用EF Code-First方式和Fluent API来探讨EF中的关系】
原文链接:http://www.c-sharpcorner.com/UploadFile/3d39b4/relationship-in-entity-framework-using-code-firs ...
- 【FastJSON】解决FastJson中“$ref 循环引用”的问题
0.开发环境 SSH,EasyUI,MySQL 1.需求要求: (1)首先获取所有的贷款订单数据,即List <LoanOrder>. (2)然后从单个贷款订单实体LoanOrder去访问 ...
- .Net Core 项目中的包引用探索(使用VSCode)
本文组织有点乱,先说结论吧: 1 在 project.json 文件中声明包引用. 而不是像以前那样可以直接引用 dll. 2 使用 dotnet restore 命令后,nuget 会把声明的依赖项 ...
- Kooboo中主要的几个关键词中的关系
Kooboo中主要的几个关键词中的关系 Content Type //相当于数据库表 Content //相当于数据 View //部分View 她可以使用Content ...
- 在SQL Server中实现关系模型的阶梯到级别3的t -SQL DML
在SQL Server中实现关系模型的阶梯到级别3的t -SQL DML 格雷戈里·拉森(Gregory Larsen),2017/08/02(第一次出版:2011 /11/09) 原文链接:http ...
- 在SQL Server中实现关系模型
使用SQL Server的Transact-SQL(T-SQL)方言,此楼梯将为您提供如何使用SQL Server表中的数据的基本了解. DML是数据操作语言,是处理数据的语言的一个方面.它包括SEL ...
随机推荐
- 实现RMQ的两种常用方法
RMQ RMQ(Range Maximum/Minimum Question)是指区间最值问题,在OI中较为常见,一般可以用ST表和线段树实现. ST表是基于倍增思想的一种打表方法,在确定区间范围和所 ...
- Xamarin.Forms XAML的辅助功能Code Snippet
Xamarin.Forms XAML的辅助功能Code Snippet 在Visual Studio中,使用Code Snippet(代码片段)功能可以减少基础代码的编写量,如常见的标签.循环语句 ...
- [CC-ANUGCD]Maximum number, GCD condition
[CC-ANUGCD]Maximum number, GCD condition 题目大意: 一个长度为\(n(n\le10^5)\)的数列\(A(A_i\le10^5)\),\(m(m\le10^5 ...
- bzoj 1231: [Usaco2008 Nov]mixup2 混乱的奶牛 -- 状压DP
1231: [Usaco2008 Nov]mixup2 混乱的奶牛 Time Limit: 10 Sec Memory Limit: 162 MB Description 混乱的奶牛 [Don Pi ...
- 2015 UESTC 搜索专题C题 基爷与加法等式 爆搜DFS
基爷与加法等式 Time Limit: 20 Sec Memory Limit: 256 MB 题目连接 http://acm.uestc.edu.cn/#/contest/show/61 Desc ...
- mybatis源码分析(6)-----核心调度对象StatmentHandler
写在前面 通过上一偏文章,我们知道:mybatis 的插件开发,主要是集中在Executor(执行器),ParameterHandler(参数处理器),ResultSetHandler(结果集处理器) ...
- gridview 空数据绑定
private void getDataBind() { DataTable dt = new DataTable(); dt.Columns.Add("id"); dt.Colu ...
- 两个不同网段的PC直连是否可以Ping通,肯定可以Ping的通(转)
在这一篇文章中http://blog.csdn.net/zhangdaisylove/article/details/46892917的案例,明确的说明两个不同网段的PC不能Ping的通,其实他给出的 ...
- Dual-voltage regulator meets USB-power needs
This Design Idea stems from the limited availability of IC voltage regulators that can meet key USB- ...
- Druid 配置_配置WebStatFilter
https://github.com/alibaba/druid/wiki/%E9%85%8D%E7%BD%AE_%E9%85%8D%E7%BD%AEWebStatFilter WebStatFilt ...
