洛谷P0248 [NOI2010] 超级钢琴 [RMQ，贪心]

　　题目传送门

超级钢琴

题目描述

小Z是一个小有名气的钢琴家，最近C博士送给了小Z一架超级钢琴，小Z希望能够用这架钢琴创作出世界上最美妙的音乐。

这架超级钢琴可以弹奏出n个音符，编号为1至n。第i个音符的美妙度为Ai，其中Ai可正可负。

一个“超级和弦”由若干个编号连续的音符组成，包含的音符个数不少于L且不多于R。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的，当且仅当这两个超级和弦所包含的音符集合是相同的。

小Z决定创作一首由k个超级和弦组成的乐曲，为了使得乐曲更加动听，小Z要求该乐曲由k个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小Z想知道他能够创作出来的乐曲美妙度最大值是多少。

输入输出格式

输入格式：

输入第一行包含四个正整数n, k, L, R。其中n为音符的个数，k为乐曲所包含的超级和弦个数，L和R分别是超级和弦所包含音符个数的下限和上限。

接下来n行，每行包含一个整数Ai，表示按编号从小到大每个音符的美妙度。

输出格式：

输出只有一个整数，表示乐曲美妙度的最大值。

输入输出样例

输入样例#1：

4 3 2 3
3
2
-6
8

输出样例#1：

11

说明

共有5种不同的超级和弦：

1.    音符1 ~ 2，美妙度为3 + 2 = 5
2.    音符2 ~ 3，美妙度为2 + (-6) = -4
3.    音符3 ~ 4，美妙度为(-6) + 8 = 2
4.    音符1 ~ 3，美妙度为3 + 2 + (-6) = -1
5.    音符2 ~ 4，美妙度为2 + (-6) + 8 = 4

最优方案为：乐曲由和弦1，和弦3，和弦5组成，美妙度为5 + 2 + 4 = 11。

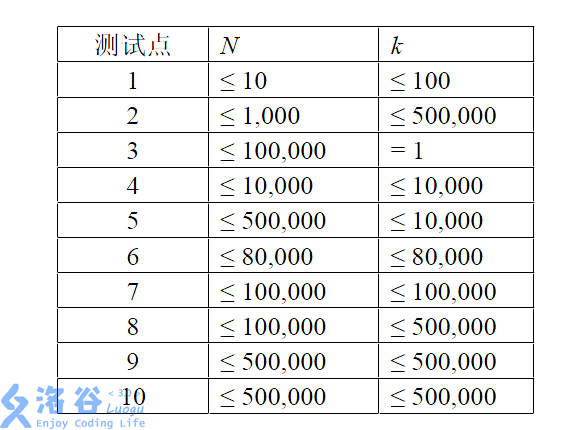
所有数据满足：-1000 ≤ Ai ≤ 1000，1 ≤ L ≤ R ≤ n且保证一定存在满足要求的乐曲。

---

　　分析：

　　一道思维比较巧妙又有点难度的题。

　　首先分析，关于这个连续子段和首先应该想到用前缀和优化，取前$k$大又可以想到用堆维护，但是如果直接做的话，复杂度还是$O(n^2)$的，那么要怎么优化呢？

　　我们可以知道，如果以$o$为左端点，那么右端点就可以是$o+L-1$到$o+R-1$，当然要保证小于$n$，那么我们能不能先把以$o$为左端点形成的所有区间的子段和最大值先预处理出来呢？这显然就是$RMQ$了。再整理以下思路我们可以得到这么一个做法：

　　用一个结构体，存储四个变量：$sta,l,r,now$，其中$sta$表示左端点，$l,r$表示右端点的范围，$now$表示以$sta$为起点时令区间子段和最大的右端点。我们用堆来维护这些结构体，每次取出最大的一个，然后更新答案，更新完答案以后最优的情况可能还在以$sta$为起点的区间里，所以我们要重新把以$sta$为起点的区间放回去，当然，这时我们就不能再把$now$放进去，所以放进去的区间应该是$(sta,(l,now-1))$，$(sta,(now+1,r))$。

　　如果不理解的话就看代码吧。

　　Code：

//It is made by HolseLee on 3rd Sep 2018
//Luogu.org P2048
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<queue>
using namespace std;

typedef long long ll;
const int N=5e5+;
int n,m,L,R,f[N][];
ll sum[N];

namespace RMQ {
    void ready()
    {
        for(int i=; i<=n; ++i) f[i][]=i;
        for(int i=; (<<i)<=n; ++i)
        for(int j=; j+(<<i)-<=n; ++j) {
            int x=f[j][i-], y=f[j+(<<(i-))][i-];
            f[j][i]=sum[x]>sum[y] ? x : y;
        }
    }

    int quary(int l,int r)
    {
        int k=log2(r-l+);
        int x=f[l][k],y=f[r-(<<k)+][k];
        return sum[x]>sum[y] ? x : y;
    }
}

struct node {
    int sta,l,r,now;
    node() {}
    node(int _o,int _l,int _r): sta(_o), l(_l), r(_r), now(RMQ::quary(_l,_r)) {}
    friend bool operator < (const node &x,const node &y) {
        return sum[x.now]-sum[x.sta-] < sum[y.now]-sum[y.sta-];
    }
};

priority_queue< node > t;

inline ll read()
{
    char ch=getchar(); ll num=; bool flag=false;
    while( ch<'' || ch>'' ) {
        if( ch=='-' ) flag=true;
        ch=getchar();
    }
    while( ch>='' && ch<='' ) {
        num=num*+ch-'';
        ch=getchar();
    }
    return flag ? -num : num;
}

int main()
{
    n=read(); m=read(); L=read(); R=read();
    for(int i=; i<=n; ++i) {
        sum[i]=read(); sum[i]+=sum[i-];
    }
    RMQ::ready();
    for(int i=; i<=n; ++i) {
        if( i+L->n ) break;
        t.push(node(i,i+L-,min(i+R-,n)));
    }
    ll ans=;
    while( m-- ) {
        int sta=t.top().sta, l=t.top().l, r=t.top().r, now=t.top().now;
        t.pop();
        ans+=sum[now]-sum[sta-];
        if( l!=now ) t.push(node(sta,l,now-));
        if( r!=now ) t.push(node(sta,now+,r));
    }
    printf("%lld\n",ans);
    return ;
}