Minimum Palindromic Factorization(最少回文串分割)

Minimum Palindromic Factorization(最少回文串分割)

以下内容大部分(可以说除了关于回文树的部分)来自论文A Subquadratic Algorithm for Minimum Palindromic Factorization。

问题描述

给出一个字符串\(S\)，将\(S\)划分为\(k\)个连续的字符串，使得每一个都是回文串，问\(k\)的最小值。

简单做法

直接做法就是\(O(n^2)\)的\(dp\)，设\(PL[i]\)表示\(S[1..i]\)划分的最小值，集合\(P_i\)表示以\(i\)为结尾的回文串的开头位置。那么

\[PL[j]=min_{i} \begin{Bmatrix} PL[i-1]+1 : i \in P_j \end{Bmatrix}
\]

而\(P_j\)可以由\(P_{j-1}\)推导出。总的时间复杂度为\(O(n^2)\).

更快的方法

如果\(P_j\)可以用另一个集合\(G_j\)代替，而\(G_j\)的大小只有\(O(logj)\)，而且在\(O(logj)\)时间内就可以从\(G_{j-1}\)推导至\(G_j\)，那么就有一个\(O(nlogn)\)的方法了。

定义1：对于一个字符串\(x\)，如果\(y\)既是\(x\)的前缀，也是\(x\)的后缀，则\(y\)称为\(x\)的一个边界，如果\(y \neq x\)，则\(y\)是一个真边界。

引理1：假设\(y\)是回文串\(x\)的一个后缀，则\(y\)是\(x\)的一个边界当且仅当\(y\)是一个回文串。

证明：

显然。

引理2：假设\(y\)是\(x\)的一个边界，且\(|x| \leq 2|y|\)，则\(x\)是一个回文串当且仅当\(y\)是回文串。

证明：

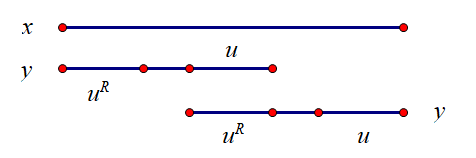
(Figure 1)

（其中\(u^R\)表示\(u\)的翻转）

定义2：假设一个字符串\(x\)，如果存在一个长度为\(p(p \leq |x|)\)的字符串\(\omega\)，满足\(x\)是\(\omega^{\infty}\)(无穷个\(\omega\)连接在一起)的一个字串，则\(p\)称为\(x\)的一个阶段。

显然，\(y\)是\(x\)的一个真边界当且仅当\(|x|-|y|\)是\(x\)的一个阶段，一并考虑引理1，能得出引理3。

引理3：设\(y\)是回文串\(x\)的一个真后缀，则\(|x|-|y|\)是\(x\)的一个阶段当且仅当\(y\)是回文串。特别地，\(|x|-|y|\)是\(x\)最小的阶段当且仅当\(y\)是\(x\)的最长的回文真后缀。

引理4：假设\(x\)是一个回文串，\(y\)是\(x\)的最长回文真后缀，\(z\)是\(y\)的最长回文真后缀，令\(x=uy, y=vz\)，则

1. \(|u| \geq |v|\)
2. 若\(|u| > |v|\)，则\(|u| > |z|\)
3. 若\(|u| = |v|\)，则\(u = v\)

证明

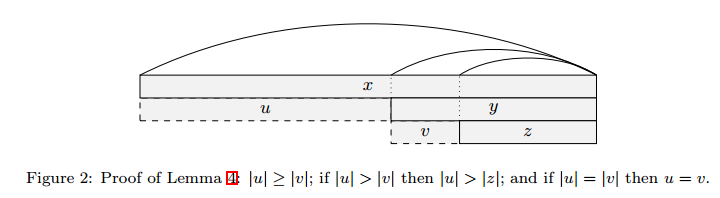
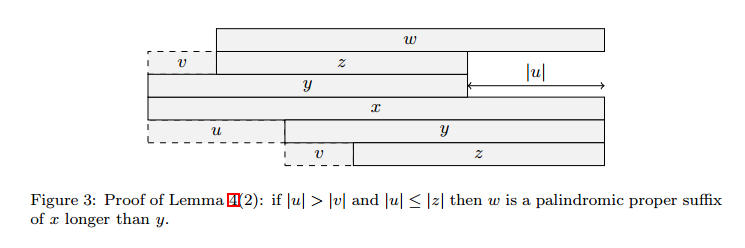
1. 由引理\(3\)得，\(|u|=|x|-|y|\)是\(x\)的最小阶段，\(|v|=|y|-|z|\)是\(y\)的最小阶段。因为\(y\)是\(x\)的子串，所以\(|u| > |y| > |v|\)或\(|u|\)也是\(y\)的一个阶段。前一个结论容易理解。当\(|u| \leq |y|\)时，由Figure 1可知重叠部分为回文串，且为\(y\)的真后缀，由引理\(3\)可知\(|u|\)是一个阶段。
2. 由引理\(1\)得，\(y\)是\(x\)的边界，\(v\)是\(x\)的前缀，设\(x=v\omega\)，则\(z\)是\(\omega\)的边界且\(|\omega|=|zu|(\because x=uvz=vzu)\)，因假设\(|u|>|v|\)，所以\(|\omega|>|y|\)。反证法：假设\(|u| \leq |z|\)，则\(|\omega|=|zu| \leq 2|z|\)，有引理\(2\)得\(\omega\)是回文串，与\(y\)为\(x\)的最长回文真后缀矛盾，得证。
3. 由2可知\(v\)是\(x\)的前缀，所以若\(|u|=|v|\)，则\(u=v\)。

利用上述引理可以得出关于\(P_j\)的一些特性，假设\(P_j=\begin{Bmatrix} p_1, p_2, ..., p_m \end{Bmatrix}, p_1<p_2<\cdots<p_m\)。\(p_i-p_{i-1}\)称为间隔。

引理5：\(P_j\)的间隔序列是不递增的，而且最多有\(O(logj)\)个不同的间隔。

证明

\(\forall i \in [2..m-1]\)(\(m\)为\(P_j\)的大小)，设\(x=S[p_{i-1}..j], y=S[p_i..j], z=S[p_{i+1}..j]\)，根据引理4，有间隔\(|u|,|v|\)。根据引理4的结论1，间隔序列是不递增的。若\(|u|>|v|\)，由引理4结论2得\(|x|>|u|+|z|>2|z|\)，即回文后缀的长度会在两步内变成一半，所以最多有\(O(logj)\)个不同的间隔。

将\(P_j\)按间隔分成\(O(logj)\)个连续的子集，每个集合的间隔相等，即设\(P_{j, \Delta}=\begin{Bmatrix} p_i: 1 < i <m, p_i-p_{i-1}=\Delta \end{Bmatrix}, P_{j, \infty}=\begin{Bmatrix} p_1 \end{Bmatrix}\)。每一个\(P_{j, \Delta}\)用一个三元组表示\((min P_{j, \Delta}, \Delta, |P_{j, \Delta}|)\)。设\(G_j\)为一个链表，以\(\Delta\)递减的顺序存在这些三元组。

\(G_j\)的大小最大为\(O(logj)\)，接下来会讲如何在\(O(|G_{j-1}|)\)时间内将\(G_{j-1}\)转移至\(G_j\)。在平方的算法中，需要对\(P_{j-1}\)的每个元素判断是去掉还是替换为减一。以下的引理可证明这一决策对\(P_{j-1, \Delta}\)能同时操作。

引理6：设\(p_i\)和\(p_{i+1}\)是\(P_{j-1, \Delta}\)的两个连续的元素，则\(p_i-1 \in P_j\)当且仅当\(p_{i+1}-1 \in P_j\)

证明

根据定义，\(p_{i+1}-p_i=\Delta\)，而且\(p_{i-1}=p_i-\Delta\)。根据引理4结论3，\(S[p_i-1]=S[p_{i+1}-1]=c\)，所以\(p_i-1 \in P_j\)当且仅当\(S[j]=c\)，即当且仅当\(p_{i+1}-1 \in P_j\)。

所以每个三元组\((i, \Delta, k) \in G_{j-1}\)或是去掉或是用\((i-1, \Delta, k)\)。即

\[G'_j=\begin{Bmatrix} (i-1, \Delta, k):(i, \Delta, k) \in G_{j-1}, i>1, and S[i-1]=S[j] \end{Bmatrix}
\]

但是\(G'_j\)可能不满足定义，因为某些间隔改变了。准确的说，当\(P_{j-1, \Delta}\)的最小元素\(p_i\)替换成了\(p_i-1\)，但\(p_{i-1}=p_i-\Delta\)被去掉了(因为\(p_{i-1}\)不符合引理4结论3，有可能\(S[p_{i-1}-1] \neq S[j]\))，则\(p_i-1\)不再属于\(P_{j, \Delta}\)。这时需要把\(p_i-1\)单独拆分，即将\((p_i-1, \Delta, k)\)分成\((p_i-1, \Delta', 1)\)和\((p_i-1+\Delta, \Delta, k-1)\)(如果\(k>1\))，其中\(\Delta'\)为新的间隔。在这过程中还需要合并相同间隔的三元组。（详细可看最后的代码）

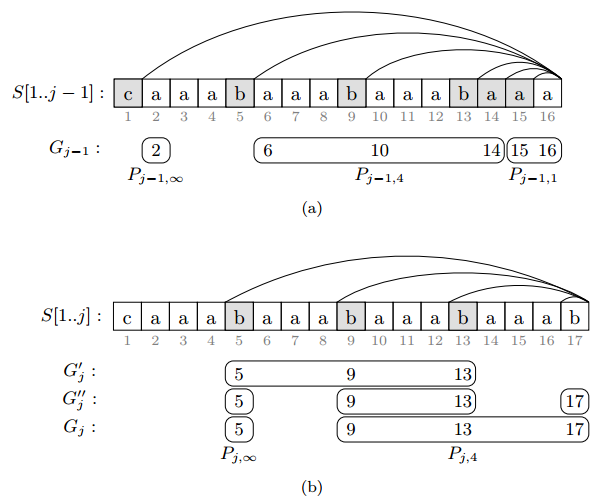
引理7：\(G_j\)能在\(O(|G_{j-1}|)=O(logj)\)时间内从\(G_{j-1}\)推导出。

接下来说明如何在\(O(|G_j|)\)的时间内，利用\(PL[j-1], G_j\)推导出\(PL[j]\)。

引理8：若\((i, \Delta, k) \in G_j, k \geq 2)\)，则\((i, \Delta, k-1) \in G_{j-\Delta}\)

证明

根据定义，\((i, \Delta, k) \in G_j\)等价于\(P_{j, \Delta}=\begin{Bmatrix} i, i+\Delta, ..., i+(k-1)\Delta \end{Bmatrix}\)，现需要证明\(P_{j-\Delta, \Delta}=\begin{Bmatrix} i, i+\Delta, ..., i+(k-2)\Delta \end{Bmatrix}\)。现在先证明\(P_{j-\Delta, \Delta} \cap [i-\Delta+1..j-\Delta]=\begin{Bmatrix} i, i+\Delta, ..., i+(k-2)\Delta \end{Bmatrix}\)，而且\(P_{j-\Delta, \Delta} \cap [1..i-\Delta]=\varnothing\)

因为\(y=S[i..j], x=S[i-\Delta..j]\)(根据\(\Delta\)的定义)都是回文串，而且\(y\)是\(x\)最长的真边界，\(S[i-\Delta..j-\Delta]=y=S[i..j]\)。所以对于\(\forall l \in [i..j], l \in P_j\)当且仅当\(l-\Delta \in P_{j-\Delta}\)。特别地，因为间隔相同，所以\(\forall l \in [i+1..j], l \in P_{j, \Delta}\)当且仅当\(l-\Delta \in P_{j-\Delta, \Delta}\)。所以\(P_{j-\Delta, \Delta} \cap [i-\Delta+1..j-\Delta]=\begin{Bmatrix} i, i+\Delta, ..., i+(k-2)\Delta \end{Bmatrix}\)。

现在还需证明\(P_{j-\Delta, \Delta} \cap [1..i-\Delta]=\varnothing\)。这为真当且仅当\(i-2\Delta \notin P_{j-\Delta}\)。反证法：\(S[i-2\Delta..j-\Delta]\)是回文串，设\(\omega=S[i-2\Delta..i-\Delta-1]\)，则\(S[j-2\Delta+1..j-\Delta]=\omega^R\)。因为\(z=S[i-\Delta..j-\Delta]\)和\(S[i-\Delta..j]\)都是回文串，所以\(S[i-\Delta..i-1]=\omega, S[j-\Delta+1..j]=\omega^R\)。因为\(z\)是回文串，所以\(S[i-2\Delta..j]=\omega z \omega^R\)也是回文串，所以\(i-2\Delta \in P_j, i-\Delta \in P_{j, \Delta}\)，矛盾，得证。而且\(i-2\Delta \notin P_{j-\Delta}\)一定成立，若\(i-2\Delta in P_{j-\Delta}\)，则\(P_{j-Delta, \Delta}\)的最小元素不是\(i\)。

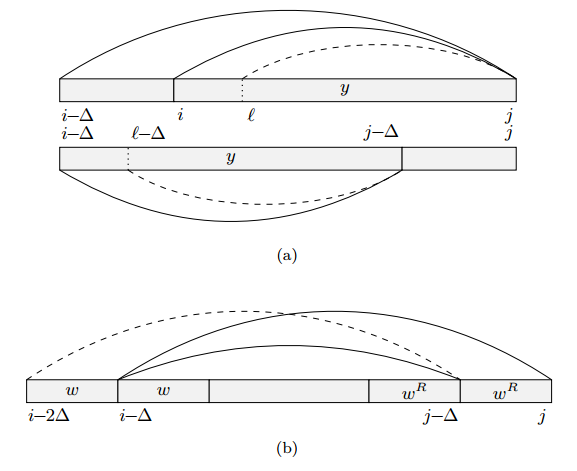
所以\(P_{j, \Delta}=P_{j-\Delta, \Delta} \cup max P_{j, \Delta}\)(当\(|P_{j, \Delta} \geq 2\))。这样\(PL_{j, \Delta}=min{PL[i-1]+1 : i \in P_{j, \Delta}}\)就能利用\(PL_{j-\Delta, \Delta}\)在常数时间内得出。

设\(GPL[i]\)，\(GPL[m=min(P_{j, \Delta}-\Delta]=PL_{j, \Delta}\)，注意到\(PL_{j-\Delta, \Delta}\)也是存在\(m\)这个位置(若\(|P_{j, \Delta} \geq 2\))。以下引理证明位置\(m\)在\((j-\Delta..j)\)不会被其它数重写。

引理9：设\(m=min(P_{j, \Delta}-\Delta), \forall l \in [j-\Delta+1..j-1], m \notin P_l\)

证明

反证法：假设\(m \in P_l, l \in [j-\Delta+1..j-1]\)，则\(S[m..l]\)是回文串，则\(S[m+h..l-h], h=l-j+\Delta\)也是回文串。因为\(l-h=j-\Delta, m<m+h<m+\Delta=min(P_{j-\Delta, \Delta})\)，所以\(m+h\)才是\(min(P_{j-\Delta, \Delta})\)在\(P_{j-\Delta}\)中的前一个，\(min(P_{j-\Delta, \Delta}) \notin P_{j-\Delta, \Delta}\)，矛盾，得证。

定理：将一个长度为\(n\)的字符串分解成最少回文串可以在时间复杂度为\(O(nlogn)\)，空间复杂度为\(O(n)\)下算出。

/*
tripe{nid, delta, sum}(开头位置， 间隔， 个数)
*/
    memset(PL, 0x7f, sizeof PL);
    memset(GPL, 0x7f, sizeof GPL);
    PL[0]=0;
    vtri G;
    G.clear();
    for (int j=1; j<=n; ++j)
    {
        vtri h;
        h.clear();
        int r=-j; //前者结尾位置
        for (auto &i : G)
            if (i.nid>1 && st[i.nid-1]==st[j])
            {
                int nid=i.nid-1;
                if (nid-r!=i.delta) //间隔不同
                {
                    //拆分
                    h.push_back(tripe{nid, nid-r, 1});
                    if (i.sum>1)
                        h.push_back(tripe{nid+i.delta, i.delta, i.sum-1});
                }
                else h.push_back(tripe{nid, i.delta, i.sum}); //间隔相同
                r=nid+(i.sum-1)*i.delta; //更新前者结尾位置
            }

        if (j>1 && st[j-1]==st[j]) //长度为2的回文串
        {
            h.push_back(tripe{j-1, j-1-r, 1});
            r=j-1;
        }
        h.push_back(tripe{j, j-r, 1}); //长度为2的回文串
        G.clear();

        //合并相同间隔的三元组
        G.push_back(*h.begin());
        for (vtri::iterator it=h.begin()+1; it!=h.end(); ++it)
            if (G.back().delta==(*it).delta) G.back().sum+=(*it).sum;
            else G.push_back(*it);

        PL[j]=j;
        for (auto &i:G)
        {
            int r=i.nid+(i.sum-1)*i.delta;
            int m=PL[r-1]+1;
            if (i.sum>1) m=min(m, GPL[i.nid-i.delta]);
            if (i.delta<=i.nid) GPL[i.nid-i.delta]=m;
            PL[j]=m;
        }
    }
    }

与回文树的结合

回文树可以维护以某个点为结尾的回文串，而且回文树中的\(fail[i]\)指向的是长度仅次于\(i\)的回文串的回文串。也就是说沿着\(fail\)走到\(root\)得到的路径就是以\(i\)为结尾的回文串，而且设\(diff\)为路径中相邻两个点的\(len\)的差，则\(diff\)就是间隔序列，而且这个间隔序列是满足上述的性质的，所以可以另外设一个数组\(anc\)来维护\(i.nid\)(同一个\(\Delta\)的开头位置)的位置，时间复杂度也是\(O(nlogn)\)。

void init() //回文树初始化
{
    S[0]=-1;
    m=0;       //字符串长度
    total=1;   //回文树点数
    last=0;    //最后插入的点
    len[0]=0;  //回文串长度
    len[1]=-1;
    fail[0]=fail[1]=1;
}
void insert(int ch)
{
    S[++m]=ch;
    int cur=last;
    while (S[m-len[cur]-1]!=S[m]) cur=fail[cur];
    if (!son[cur][ch])
    {
        len[++total]=len[cur]+2;
        int tmp=fail[cur];
        while (S[m-len[tmp]-1]!=S[m]) tmp=fail[tmp];
        tmp=son[tmp][ch];
        fail[total]=tmp; son[cur][ch]=total;
        diff[total]=len[total]-len[tmp]; //间隔序列
        anc[total]=(diff[total]==diff[tmp]? anc[tmp]:tmp); //开头位置
    }
    last=son[cur][ch];
}
void solve()
{
    init();
    for (int i=1; i<=n; ++i) ans[i]=inf;
    for (int i=1; i<=n; ++i)
    {
        insert(a[i]);
        for (int j=last; j; j=anc[j])
        {
            hd[j]=i-len[anc[j]]-diff[j]; //GPL存放位置
            if (anc[j]!=fail[j] && ans[hd[fail[j]]]<ans[hd[j]])
                hd[j]=hd[fail[j]];
            if (!(i & 1) && ans[hd[j]]+1<ans[i]) ans[i]=ans[hd[j]]+1;
        }
    }
}