小x的质数（线性O（n）筛素数）

小x的质数

题目描述

小 X 是一位热爱数学的男孩子，在茫茫的数字中，他对质数更有一种独特的情感。小 X 认为，质数是一切自然数起源的地方。

在小 X 的认知里，质数是除了本身和 11 以外，没有其他因数的数字。

但由于小 X 对质数的热爱超乎寻常，所以小 X 同样喜欢那些虽然不是质数，但却是由两个质数相乘得来的数。

于是，我们定义，一个数是小 X 喜欢的数，当且仅当其是一个质数，或是两个质数的乘积。

而现在，小 X 想要知道，在 LL 到 RR 之间，有多少数是他喜欢的数呢？

输入格式

第一行输入一个正整数 QQ，表示询问的组数。

接下来 QQ 行。包含两个正整数 LL 和 RR。保证 L \le RL≤R。

输出格式

输出 QQ 行，每行一个整数，表示小 X 喜欢的数的个数。

数据范围与约定

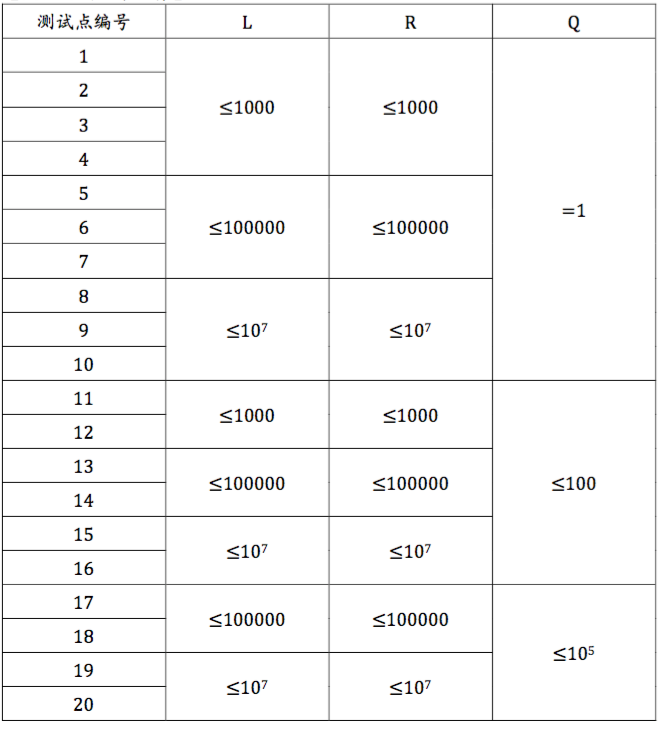
样例

样例解释 1

66 以内的质数有 2,3,52,3,5，而 4=2 * 2,6 = 2 * 34=2∗2,6=2∗3。因此 2,3,4,5,62,3,4,5,6 都是小 X 喜 欢的数，而 1 不是。

样例输入1

1
1 6

样例输出1

5

样例输入2

10
282 491
31 178
645 856
227 367
267 487
474 697
219 468
582 792
315 612
249 307

样例输出2

97
78
92
65
102
98
114
90
133
29

样例输入3

10
20513 96703
15236 86198
23185 78205
40687 48854
42390 95450
63915 76000
36793 92543
35347 53901
44188 76922
82177 90900

样例输出3

24413
23001
17784
2669
16785
3833
17712
6028
10442
2734

code

 #include<cstdio>
 #include<cmath>

 const int MAXN = ;

 bool lk[MAXN],noprime[MAXN];
 int prime[MAXN];
 int sum[MAXN];

 int read() {
     int x = ,f = ;char ch = getchar();
     for (; ch<''||ch>''; ch = getchar())
         if (ch=='-') f = -;
     for (; ch>=''&&ch<=''; ch = getchar())
         x = x*+ch-'';
     return x*f;
 }

 int main() {

     int tot = ;

     for (int i=; i<=; i++) {
         if (!noprime[i]) {
             prime[++tot]=i;
             lk[i] = true;
             for (int j=; j<=tot && i*prime[j]<=; j++) {
                 noprime[i*prime[j]] = true;
                 lk[i*prime[j]] = true;
             }
         }
         else {
             for (int j=; j<=tot&&i*prime[j]<=; j++) {
                 noprime[i*prime[j]] = true;
                 if(i % prime[j] == ) break ;
             }
         }
     }

     for (int i=; i<=; ++i) {
         if (lk[i]) sum[i] = sum[i-]+;
         else sum[i] = sum[i-];
     }

     int L,R,q = read();
     while (q--) {
         L = read();R = read();
         printf("%d\n",sum[R]-sum[L-]);
     }

     return ;
 }