2014 Noip提高组 Day1

P1328 生活大爆炸版石头剪刀布

【题目描述】

石头剪刀布是常见的猜拳游戏：石头胜剪刀，剪刀胜布，布胜石头。如果两个人出拳一样，则不分胜负。在《生活大爆炸》第二季第8 集中出现了一种石头剪刀布的升级版游戏。

升级版游戏在传统的石头剪刀布游戏的基础上，增加了两个新手势：

斯波克：《星际迷航》主角之一。

蜥蜴人：《星际迷航》中的反面角色。

这五种手势的胜负关系如表一所示，表中列出的是甲对乙的游戏结果。

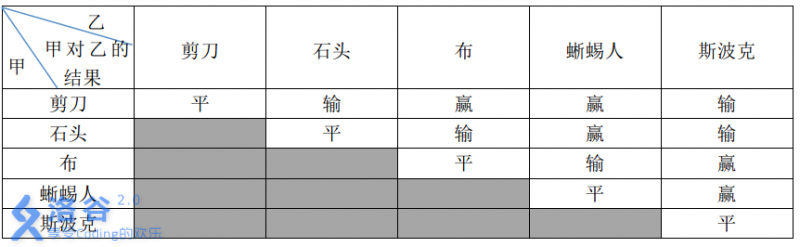
现在，小A 和小B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的，但周期长度不一定相等。例如：如果小 A以“石头 - 布- 石头- 剪刀- 蜥蜴人- 斯波克”长度为6 的周期出拳，那么他的出拳序列就是“石头- 布- 石头- 剪刀- 蜥蜴人- 斯波克- 石头- 布- 石头- 剪刀- 蜥蜴人- 斯波克- ……”，而如果小B 以“剪刀- 石头- 布- 斯波克- 蜥蜴人”长度为5 的周期出拳，那么他出拳的序列就是“剪刀- 石头- 布- 斯波克- 蜥蜴人- 剪刀- 石头- 布-斯波克- 蜥蜴人- ……”

已知小A 和小B 一共进行N 次猜拳。每一次赢的人得1 分，输的得0 分；平局两人都得0 分。现请你统计N 次猜拳结束之后两人的得分。

【输入输出格式】

输入格式：

输入文件名为rps.in。

第一行包含三个整数：N ，NA，NB，分别表示共进行 N 次猜拳、小 A 出拳的周期长度，小B 出拳的周期长度。数与数之间以一个空格分隔。

第二行包含NA个整数，表示小 A 出拳的规律，第三行包含NB个整数，表示小 B 出拳的规律。其中，0 表示“剪刀”，1 表示“石头”，2 表示“布”，3 表示“蜥蜴人”， 4 表示“斯波克”。数与数之间以一个空格分隔。

输出格式：

输出文件名为rps.out 。

输出一行，包含两个整数，以一个空格分隔，分别表示小A 、小B 的得分。

【输入输出样例】

输入样例#1：

10 5 6

0 1 2 3 4

0 3 4 2 1 0

输出样例#1：

6 2

输入样例#2：

输出样例#2：

4 4

【说明】

对于100%的数据，0 < N ≤ 200 ，0 < NA ≤ 200 ， 0 < NB ≤ 200 。

#include<iostream>

#include<cstdio>

using namespace std;

int n,n1,n2,map[][],a[],b[];

int main(){

    scanf("%d%d%d",&n,&n1,&n2);

    for(int i=;i<=n1;i++)scanf("%d",&a[i]);

    for(int i=;i<=n2;i++)scanf("%d",&b[i]);

    for(int i=;i<=;i++)map[i][i]=;

    map[][]=;map[][]=;map[][]=;map[][]=;map[][]=;

    map[][]=;map[][]=;map[][]=;map[][]=;map[][]=;

    int cnt1=,cnt2=,ans1=,ans2=;

    for(int i=;i<=n;i++){

        cnt1++;cnt2++;

        if(cnt1>n1)cnt1=;

        if(cnt2>n2)cnt2=;

        ans1+=map[a[cnt1]][b[cnt2]];

        ans2+=map[b[cnt2]][a[cnt1]];

    }

    printf("%d %d",ans1,ans2);

}

100分模拟

P1351 联合权值

【题目描述】

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

【输入输出格式】

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

【输入输出样例】

输入样例#1：

输出样例#1：

20 74

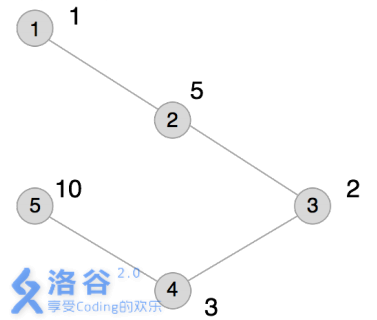
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

/*

    由于所给的图是一棵树，所以与某一点可以联合权值的点应该是它父亲节点的其他儿子节点，他的爷爷节点和他儿子的儿子节点，对于最终答案来说，某点的儿子的儿子节点和父亲的父亲节点可以算做一个

*/

#include<iostream>

#include<cstdio>

#define maxn 200010

#define mod 10007

#define LL long long

using namespace std;

int ans1,ans;

int n,num,head[maxn],fa1[maxn],fa2[maxn],w[maxn];

struct node{

    int to,pre;

}e[maxn*];

void Insert(int from,int to){

    e[++num].to=to;

    e[num].pre=head[from];

    head[from]=num;

}

void dfs1(int father,int now){

    fa1[now]=father;fa2[now]=fa1[father];

    int t=w[now]*w[fa2[now]];

    ans1=max(ans1,t);

    ans=(ans+1LL**t%mod)%mod;

    for(int i=head[now];i;i=e[i].pre){

        int to=e[i].to;

        if(to==father)continue;

    }

}

int main(){

    scanf("%d",&n);

    int x,y;

    for(int i=;i<n;i++){

        scanf("%d%d",&x,&y);

        Insert(x,y);

        Insert(y,x);

    }

    for(int i=;i<=n;i++)scanf("%d",&w[i]);

    dfs1(,);

    for(int i=;i<=n;i++){

        for(int j=head[i];j;j=e[j].pre){

            int to1=e[j].to;

            for(int k=head[i];k;k=e[k].pre){

                int to2=e[k].to;

                if(to1==to2)continue;

                int t=w[to1]*w[to2];

                ans1=max(ans1,t);

                ans=(ans+t%mod)%mod;

            }

        }

    }

    cout<<ans1<<' '<<ans;

}

70分暴力

/*

        这个题取模特别容易出问题

        设sum[i]表示与点i直接相连的点权和

    可以发现，对于每个点i，它对联值权值之和的贡献=w[i]*sum[j] （j是与i直接相连的点）

    令maxn[i]表示与i直接相连的点中，最大的点权和

    那么对于i，最大的联合权值=w[i]*max（maxn[j]）（j是与i直接相连的点）

    注意我们在计算最大的联合权值时，maxn[j]可能就是点i的权值，不合法

    所以同时记录maxn[j]是哪个点的点权，同时记录一个次大点权maxn_[j]

    统计答案时，枚举点i，枚举与i直接相连的点j，若maxn[j]对应得点=i，用次大点权来算

*/

#include<iostream>

#include<cstdio>

using namespace std;

#define maxn 200010

#define mod 10007

int num,head[maxn],n,w[maxn],m1[maxn],m2[maxn],mt[maxn];

long long ans1,sum[maxn];

int ans2;

struct node{

    int to,pre;

}e[maxn*];

void Insert(int from,int to){

    e[++num].to=to;

    e[num].pre=head[from];

    head[from]=num;

}

int main(){

    //freopen("Cola.txt","r",stdin);

    scanf("%d",&n);

    int x,y;

    for(int i=;i<n;i++){

        scanf("%d%d",&x,&y);

        Insert(x,y);

        Insert(y,x);

    }

    for(int i=;i<=n;i++)scanf("%d",&w[i]);

    for(int i=;i<=n;i++){

        for(int j=head[i];j;j=e[j].pre){

            int to=e[j].to;

            sum[i]=(sum[i]+w[to])%mod;

            if(w[to]>=m1[i]){

                m2[i]=m1[i];

                m1[i]=w[to];

                mt[i]=to;

            }

            else m2[i]=max(m2[i],w[to]);

        }

    }

    for(int i=;i<=n;i++){

        int mx=;

        for(int j=head[i];j;j=e[j].pre){

            int to=e[j].to;

            ans1=(ans1+(1LL*w[i]*(sum[to]-w[i]))%mod)%mod;

            int k=m1[to];

            if(mt[to]==i)k=m2[to];

            mx=max(k*w[i],mx);

        }

        ans2=max(ans2,mx);

    }

    cout<<ans2<<' '<<ans1;

}

100分

P1941 飞扬的小鸟

【题目描述】

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编：

游戏界面是一个长为n ，高为 m 的二维平面，其中有k 个管道（忽略管道的宽度）。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为1 ，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度X ，每个单位时间可以点击多次，效果叠加；

如果不点击屏幕，小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时，上升的高度X 和下降的高度Y 可能互不相同。

小鸟高度等于0 或者小鸟碰到管道时，游戏失败。小鸟高度为 m 时，无法再上升。

现在，请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

【输入输出格式】

输入格式：

输入文件名为 bird.in 。

第1 行有3 个整数n ，m ，k ，分别表示游戏界面的长度，高度和水管的数量，每两个

整数之间用一个空格隔开；

接下来的n 行，每行2 个用一个空格隔开的整数X 和Y ，依次表示在横坐标位置0 ~n- 1

上玩家点击屏幕后，小鸟在下一位置上升的高度X ，以及在这个位置上玩家不点击屏幕时，

小鸟在下一位置下降的高度Y 。

接下来k 行，每行3 个整数P ，L ，H ，每两个整数之间用一个空格隔开。每行表示一

个管道，其中P 表示管道的横坐标，L 表示此管道缝隙的下边沿高度为L ，H 表示管道缝隙

上边沿的高度（输入数据保证P 各不相同，但不保证按照大小顺序给出）。

输出格式：

输出文件名为bird.out 。

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出1 ，否则输出0 。

第二行，包含一个整数，如果第一行为1 ，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

【输入输出样例】

输入样例#1：

输出样例#1：

1

6

输入样例#2：

输出样例#2：

0

3

【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

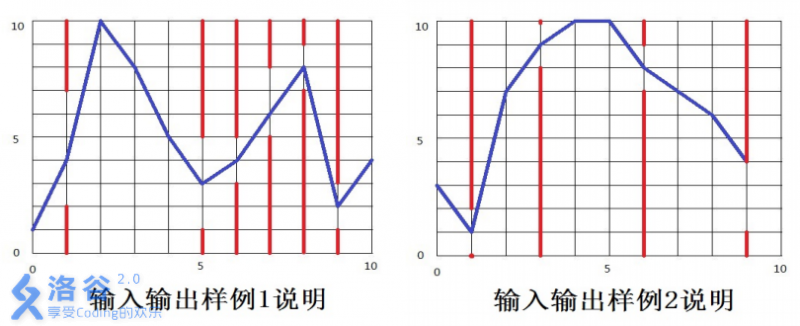
【数据范围】

对于30% 的数据：5 ≤ n ≤ 10，5 ≤ m ≤ 10，k = 0 ，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于50% 的数据：5 ≤ n ≤ 2 0 ，5 ≤ m ≤ 10，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于70% 的数据：5 ≤ n ≤ 1000，5 ≤ m ≤ 1 0 0 ；

对于100%的数据：5 ≤ n ≤ 100 0 0 ，5 ≤ m ≤ 1 0 00，0 ≤ k < n ，0<X < m ，0<Y <m，0<P <n，0 ≤ L < H ≤ m ，L +1< H 。

#include<iostream>

#include<cstdio>

using namespace std;

#define maxn 10010

int n,m,cdt,ans=0x7fffffff,ans1;

bool flag,th[maxn];

struct node{

    int x,y;

}p[maxn];

struct Node{

    int l,h;

}c[maxn];

void dfs(int now,int hi,int cnt,int step){

    if(cnt>ans)return;

    if(now==n){

        ans=min(ans,cnt);

        flag=;

        return;

    }

    ans1=max(ans1,step);

    if(hi-p[now].y<c[now+].h&&hi-p[now].y>c[now+].l){//说明可以不点击

        if(th[now+]){//下一秒要到达的地方有管道

            dfs(now+,hi-p[now].y,cnt,step+);

        }

        else dfs(now+,hi-p[now].y,cnt,step);

    }

    int sum=;

    while(){

        hi+=p[now].x;sum++;

        if(hi>m)hi=m;

        if(hi>=c[now+].h)break;

        if(hi<=c[now+].l)continue;

        if(th[now+]){

            dfs(now+,hi,cnt+sum,step+);

        }

        else {

            dfs(now+,hi,cnt+sum,step);

        }

        if(hi==m)return;

    }

}

int main(){

    //freopen("Cola.txt","r",stdin);

    scanf("%d%d%d",&n,&m,&cdt);

    for(int i=;i<=n;i++)c[i].l=,c[i].h=m+;

    for(int i=;i<n;i++)scanf("%d%d",&p[i].x,&p[i].y);

    int u,v,w;

    for(int i=;i<=cdt;i++){

        scanf("%d%d%d",&u,&v,&w);

        c[u].l=v;c[u].h=w;

        th[u]=;

    }

    for(int i=;i<=m;i++)dfs(,i,,);

    if(flag){//能到达终点

        printf("1\n");

        printf("%d",ans);

    }

    else {

        printf("0\n");

        printf("%d",ans1);

    }

}

50分暴力

/*

    50分做法：暴力dfs

    70分做法：

    向上的是完全背包，向下的是01背包

    令f[i][j]表示到达横坐标为i，高度为j的最小点击数

    向上的状态转移方程：f[i][j]=min( f[i-1][j-up[i-1]*k]+k )   k<=m/up[i-1]

    向下的状态转移方程：f[i][j]=min( f[i-1][j+down[i-1]])

    时间复杂度：O（nm2）

    100分做法：

    在向上的状态转移方程中，

    若p=j-up[i-1]*k， 那么到达状态p 和 到达状态j 的 很多起点是重复的

    也就是说，由重复的相同状态转移到了不同状态

    优化这个重复的相同状态

    假设一次上升高度x

        f[i][j-x]= min（ f[i-1][ (j-x)-x*(k-1) ]+k-1 ）

        原式:f[i][j]=min（ f[i-1][j-x*k]+k）

    发现 当k>1时，f[i][j]=f[i][j-x]+1

    所以新的向上的状态转移方程：f[i][j]=min（f[i-1][j-x],f[i][j-x]）+1

*/

#include<cstdio>

#include<algorithm>

#define N 10001

#define inf 20001

using namespace std;

int n,m,k,ok;

int up[N],down[N],top[N],bot[N];

int f[N][];

bool have[N];

int main() {

    scanf("%d%d%d",&n,&m,&k);

    int x;

    for(int i=; i<n; i++) scanf("%d%d",&up[i],&down[i]);

    for(int i=; i<=k; i++) {

        scanf("%d",&x);

        have[x]=true;

        scanf("%d%d",&bot[x],&top[x]);

    }

    for(int i=; i<=n; i++)

        if(!top[i]) top[i]=m+;

    for(int i=; i<=n; i++)

        for(int j=; j<=m; j++)

            f[i][j]=inf;

    //for(int i=0; i<=m; i++) f[0][i]=0;

    for(int i=; i<=bot[]; i++) f[][i]=inf;

    for(int i=top[]; i<=m; i++) f[][i]=inf;

    for(int i=; i<=n; i++) {

        for(int j=up[i-]+; j<=m; j++) f[i][j]=min(f[i-][j-up[i-]],f[i][j-up[i-]])+;

        for(int j=m-up[i-]; j<=m; j++) f[i][m]=min(f[i][m],min(f[i][j],f[i-][j])+);

        for(int j=; j<=m-down[i-]; j++) f[i][j]=min(f[i][j],f[i-][j+down[i-]]);

        for(int j=; j<=bot[i]; j++) f[i][j]=inf;

        for(int j=top[i]; j<=m; j++) f[i][j]=inf;

        if(!have[i]) continue;

        int j;

        for(j=bot[i]+; j<=top[i]; j++)

            if(f[i][j]<inf) {

                ok++;

                break;

            }

        if(j>top[i]) {

            printf("0\n%d",ok);

            return ;

        }

    }

    int sum=inf;

    for(int i=; i<=m; i++) sum=min(sum,f[n][i]);

    printf("1\n%d",sum);

}

100分 dp