BZOJ 1201 [HNOI2005]数三角形：枚举 + 前缀和

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1201

题意：

　　有一个边长为n的正三角形网格，去掉其中一些线段，问你在这幅图中有多少个三角形。

题解：

　　枚举 + 前缀和。

　　三角形总共有两种：正着放的、倒着放的。

　　分别处理就好。

　　总复杂度 < O(N^3)

　　为了判断某一个三角形是否存在，需要迅速判断它的三边是否都是实线（不断开）。

　　所以建立三个前缀和，分别代表左、右、底边在对应方向上的边长和。

　　若某一边上的区间和[a,b] == b-a+1，则为实线。

　　如图为前缀和方向：

　　

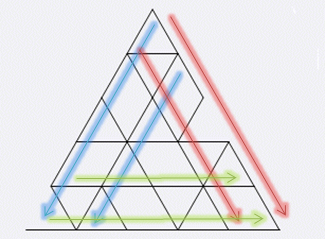
　　正着放的：

　　　　N^2枚举三角形最顶上的小三角形，再套一个for枚举向下延伸的边长k。

　　

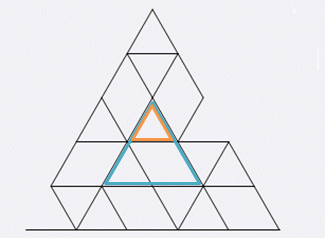
　　倒着放的：

　　　　倒三角形底部有一个小倒三角形，枚举它左边相邻的小正三角。

　　

AC Code:

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #define MAX_N 1005

 using namespace std;

 int n;
 int ans=;
 int l[MAX_N][MAX_N];
 int r[MAX_N][MAX_N];
 int b[MAX_N][MAX_N];
 int lef[MAX_N][MAX_N];
 int rig[MAX_N][MAX_N];
 int btm[MAX_N][MAX_N];

 void read()
 {
     memset(l,,sizeof(l));
     memset(r,,sizeof(r));
     memset(b,,sizeof(b));
     cin>>n;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=i;j++)
         {
             cin>>l[i][j]>>r[i][j]>>b[i][j];
         }
     }
 }

 void cal_sum()
 {
     memset(lef,,sizeof(lef));
     memset(rig,,sizeof(rig));
     memset(btm,,sizeof(btm));
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=i;j++)
         {
             lef[i][j]=lef[i-][j]+l[i][j];
             rig[i][j]=rig[i-][j-]+r[i][j];
             btm[i][j]=btm[i][j-]+b[i][j];
         }
     }
 }

 void find_tri()
 {
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=i;j++)
         {
             for(int k=;;k++)
             {
                 if(lef[i+k-][j]-lef[i-][j]<k) break;
                 if(rig[i+k-][j+k-]-rig[i-][j-]<k) break;
                 if(btm[i+k-][j+k-]-btm[i+k-][j-]<k) continue;
                 ans++;
             }
         }
     }
     for(int i=;i<=n;i++)
     {
         for(int j=;j<i;j++)
         {
             for(int k=;i-k>= && j-k>=;k++)
             {
                 if(lef[i][j+]-lef[i-k][j+]<k) break;
                 if(rig[i][j]-rig[i-k][j-k]<k) break;
                 if(btm[i-k][j]-btm[i-k][j-k]<k) continue;
                 ans++;
             }
         }
     }
 }

 void solve()
 {
     cal_sum();
     find_tri();
 }

 void print()
 {
     cout<<ans<<endl;
 }

 int main()
 {
     read();
     solve();
     print();
 }