SVM用于线性回归

SVM用于线性回归

方法分析

在样本数据集（）中，不是简单的离散值，而是连续值。如在线性回归中，预测房价。与线性回归类型，目标函数是正则平方误差函数：

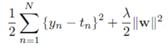
在SVM回归算法中，目的是训练出超平面，采用作为预测值。为了获得稀疏解，即计算超平面参数w,b不依靠所有样本数据，而是部分数据（如在SVM分类算法中，支持向量的定义），采用误差函数

误差函数定义为，如果预测值与真实值的差值小于阈值将不对此样本做惩罚，若超出阈值，惩罚量为。

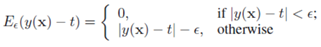
下图为误差函数与平方误差函数的图形

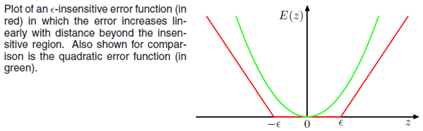
目标函数

观察上述的误差函数的形式，可以看到，实际形成了一个类似管道的样子，在管道中样本点，不做惩罚，所以被称为,如下图阴影红色部分

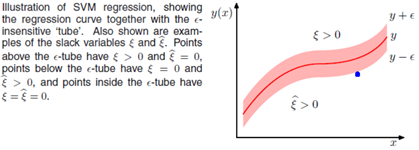
用替代平方误差项，因此可以定义最小化误差函数作为优化目标：

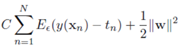
由于上述目标函数含有绝对值项不可微。我们可以转化成一个约束优化问题，常用的方法是为每一个样本数据定义两个松弛变量,表示度量与的距离。

如上图所示：

当样本点真实值位于管道上方时，写成表达式：时，

当样本点真实值位于管道下方时，写成表达式：时，

因此使得每个样本点位于管道内部的条件为：

当位于管道上方时，，有

当位于管道下方时，，有

误差函数可以写成为一个凸二次优化问题：

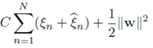
约束条件为：

写成拉格朗日函数：

对偶问题

上述问题为极小极大问题

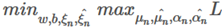
与SVM分类分析方法一样，改写成对偶问题

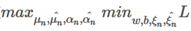
首先求偏导数

超平面计算

Support Vector Machine - Regression (SVR)

Support Vector Machine can also be used as a regression method, maintaining all the main features that characterize the algorithm (maximal margin). The Support Vector Regression (SVR) uses the same principles as the SVM for classification, with only a few minor differences. First of all, because output is a real number it becomes very difficult to predict the information at hand, which has infinite possibilities. In the case of regression, a margin of tolerance (epsilon) is set in approximation to the SVM which would have already requested from the problem. But besides this fact, there is also a more complicated reason, the algorithm is more complicated therefore to be taken in consideration. However, the main idea is always the same: to minimize error, individualizing the hyperplane which maximizes the margin, keeping in mind that part of the error is tolerated.

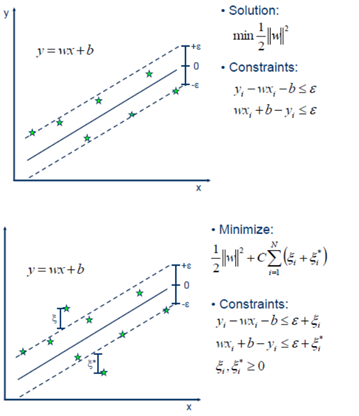
Linear SVR

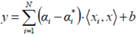
Non-linear SVR

The kernel functions transform the data into a higher dimensional feature space to make it possible to perfom the linear separation

Kernel functions