2.融合进阶：Stacking与Blending

1 堆叠法Stacking

1.1 堆叠法的基本思想

堆叠法Stacking是近年来模型融合领域最为热门的方法，它不仅是竞赛冠军队最常采用的融合方法之一，也是工业中实际落地人工智能时会考虑的方案之一。作为强学习器的融合方法，Stacking集模型效果好、可解释性强、适用复杂数据三大优点于一身，属于融合领域最为实用的先驱方法。在Stacking的众多应用当中，CTR（广告点击率预测）中实用的GBDT+LR堆叠尤为著名。因此在《2022机器学习实战》正课当中，讲解完毕通用的stacking手段之后，我会给大家详细讲解GBDT+LR在CTR中的用法，并完成一个CTR实战。

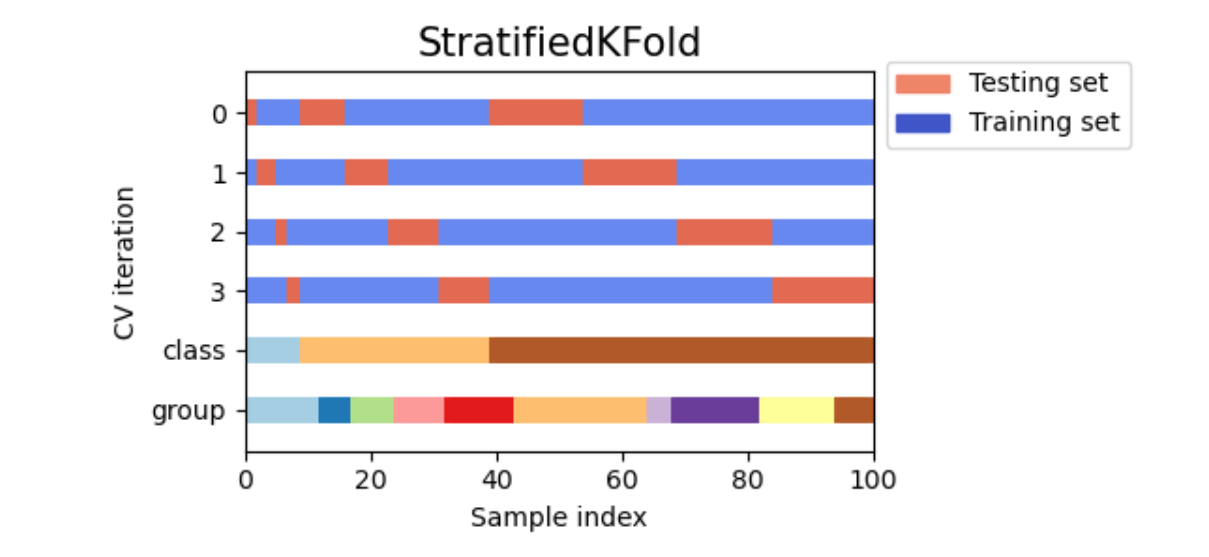
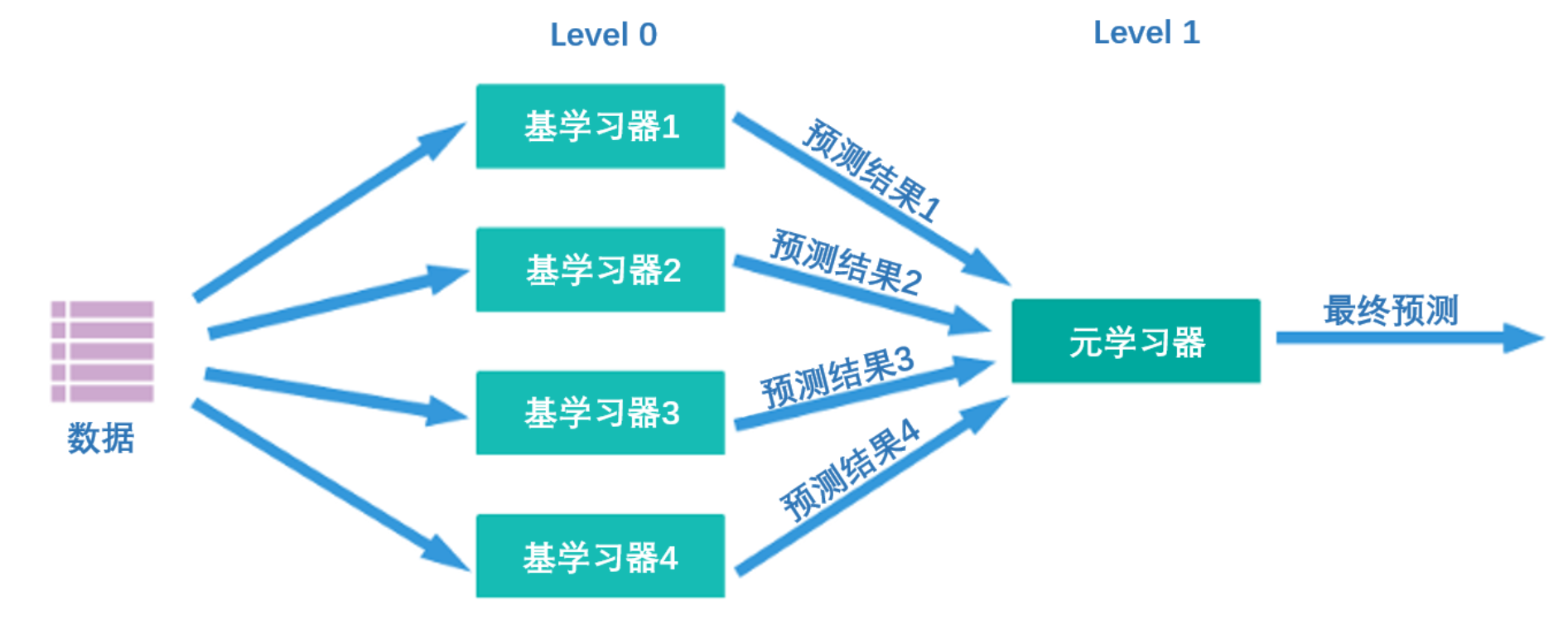
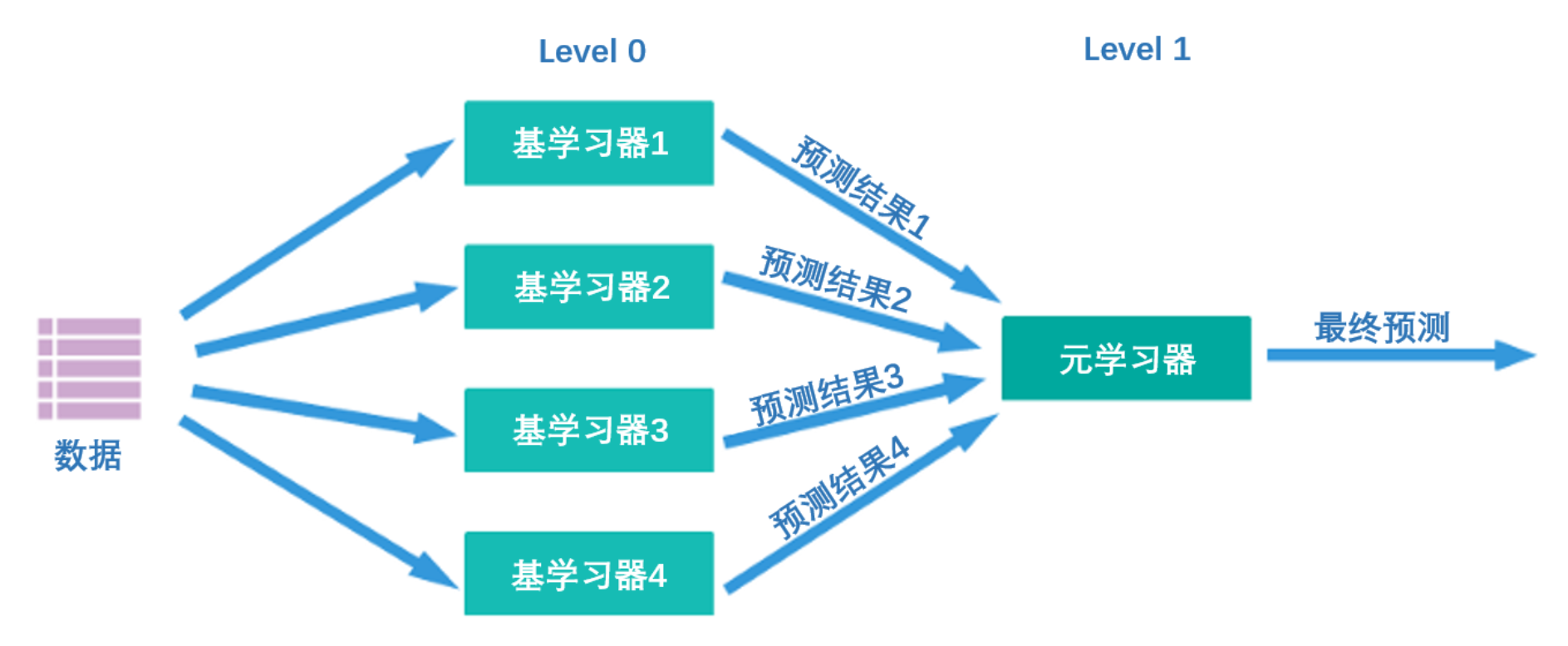
Stacking究竟是怎样一种算法呢？它的核心思想其实非常简单——首先，如下图所示，Stacking结构中有两层算法串联，第一层叫做level 0，第二层叫做level 1，level 0里面可能包含1个或多个强学习器，而level 1只能包含一个学习器。在训练中，数据会先被输入level 0进行训练，训练完毕后，level 0中的每个算法会输出相应的预测结果。我们将这些预测结果拼凑成新特征矩阵，再输入level 1的算法进行训练。融合模型最终输出的预测结果就是level 1的学习器输出的结果。

在这个过程中，level 0输出的预测结果一般如下排布：

	学习器1	学习器2	...	学习器n
样本1	xxx	xxx	...	xxx
样本2	xxx	xxx	...	xxx
样本3	xxx	xxx	...	xxx
...	...	...	...	...
样本m	xxx	xxx	...	xxx

第一列就是学习器1在全部样本上输出的结果，第二列就是学习器2在全部样本上输出的结果，以此类推。

同时，level 0上训练的多个强学习器被称为基学习器(base-model)，也叫做个体学习器。在level1上训练的学习器叫元学习器（meta-model）。根据行业惯例，level 0上的学习器是复杂度高、学习能力强的学习器，例如集成算法、支持向量机，而level 1上的学习器是可解释性强、较为简单的学习器，如决策树、线性回归、逻辑回归等。有这样的要求是因为level 0上的算法们的职责是找出原始数据与标签的关系、即建立原始数据与标签之间的假设，因此需要强大的学习能力。但level 1上的算法的职责是融合个体学习器做出的假设、并最终输出融合模型的结果，相当于在寻找“最佳融合规则”，而非直接建立原始数据与标签之间的假设。

说到这里，不知道你是否有注意到，Stacking的本质是让算法找出融合规则。虽然大部分人可能从未接触过类似于Stacking算法的串联结构，但事实上Stacking的流程与投票法、均值法完全一致：

在投票法中，我们用投票方式融合强学习器的结果，在均值法中，我们用求均值方式融合强学习器的结果，在Stacking堆叠法中，我们用算法融合强学习器的结果。当level 1上的算法是线性回归时，其实我们就是在求解所有强学习器结果的加权求和，而训练线性回归的过程，就是找加权求和的权重的过程。同样的，当level 1上的算法是逻辑回归的时候，其实我们就是在求解所有强学习器结果的加权求和，再在求和基础上套上sigmoid函数。训练逻辑回归的过程，也就是找加权求和的权重的过程。其他任意简单的算法同理。

虽然对大多数算法来说，我们难以找出类似“加权求和”这样一目了然的名字来概括算法找出的融合规则，但本质上，level 1的算法只是在学习如何将level 0上输出的结果更好地结合起来，所以Stacking是通过训练学习器来融合学习器结果的方法。均值法是将输出结果平均，投票法是将输出结果投票，前面这两种都是人为定义融合方法，但是这个Stacking是让机器帮我们找到一个最佳的融合方法。 这一方法的根本优势在于，我们可以让level 1上的元学习器向着损失函数最小化的方向训练，而其他融合方法只能保证融合后的结果有一定的提升。因此Stacking是比Voting和Averaging更有效的方法。在实际应用时，Stacking也常常表现出胜过投票或均值法的结果。

当我们了解了Stacking的本质之后，很多实现过程中的细节问题就迎刃而解了，比如：

• 要不要对融合的算法进行精密的调参？

个体学习器粗调，元学习器精调，如果不过拟合的话，可以两类学习器都精调。理论上来说，算法输出结果越接近真实标签越好，但个体学习器精调后再融合，很容易过拟合。

• 个体学习器算法要怎样选择才能最大化stacking的效果？

与投票、平均的状况一致，控制过拟合、增加多样性、注意算法整体的运算时间。

• 个体学习器可以是逻辑回归、决策树这种复杂度较低的算法吗？元学习器可以是xgboost这种复杂度很高的算法吗？

都可以，一切以模型效果为准。对level 0而言，当增加弱学习器来增加模型多样性、且弱学习器的效果比较好时，可以保留这些算法。对level 1而言，只要不过拟合，可以使用任何算法。个人推荐，在分类的时候可以使用复杂度较高的算法，对回归最好还是使用简单的算法。

• level 0和level 1的算法可不可以使用不同的损失函数？

可以，因为不同的损失函数衡量的其实是类似的差异：即真实值与预测值之间的差异。不过不同的损失对于差异的敏感性不同，如果可能的话建议使用相似的损失函数。

• level 0和level 1的算法可不可以使用不同的评估指标？

个人建议level 0与level 1上的算法必须使用相同的模型评估指标。虽然Stacking中串联了两组算法，但这两组算法的训练却是完全分离的。在深度学习当中，我们也有类似的强大算法串联弱小算法的结构，例如，卷积神经网络就是由强大的卷积层与弱小的线性层串联，卷积层的主要职责是找出特征与标签之间的假设，而线性层的主要职责是整合假设、进行输出。但在深度学习中，一个网络上所有层的训练是同时进行的，每次降低损失函数时需要更新整个网络上的权重。但在Stacking当中，level 1上的算法在调整权重时，完全不影响level 0的结果，因此为了保证两组算法最终融合后能够得到我们想要的结果，在训练时一定要以唯一评估指标为基准进行训练。

2 在sklearn中实现stacking

class sklearn.ensemble.StackingClassifier(

estimators,

final_estimator=None, *,

cv=None,

stack_method='auto',

n_jobs=None,

passthrough=False,

verbose=0)

class sklearn.ensemble.StackingRegressor(

estimators,

final_estimator=None,*,

cv=None,

n_jobs=None,

passthrough=False,

verbose=0)

参数	说明
estimators	个体评估器的列表。在sklearn中，只使用单一评估器作为个体评估器时， 模型可以运行，但效果往往不太好。
final_estimator	元学习器，只能有一个评估器。当融合模型执行分类任务时，元学习器一定是分类算法， 当融合模型执行回归任务时，元学习器一定是回归算法。
cv	用于指定交叉验证的具体类型、折数等细节。 可以执行简单的K折交叉验证，也可以输入sklearn中交叉验证类。
stack_method	只有分类器才有的参数，表示个体学习器输出的具体测试结果。
passthrough	在训练元学习器时，是否加入原始数据作为特征矩阵。
n_jobs, verbose	线程数与监控参数。

在sklearn当中，只要输入estimators和final_estimator，就可以执行stacking了。我们可以沿用在投票法中使用过的个体学习器组合，并使用随机森林作为元学习器来完成stacking：

• 工具库 & 数据

#常用工具库
import re
import numpy as np
import pandas as pd
import matplotlib as mlp
import matplotlib.pyplot as plt
import time

#算法辅助 & 数据
import sklearn
from sklearn.model_selection import KFold, cross_validate
from sklearn.datasets import load_digits #分类 - 手写数字数据集
from sklearn.datasets import load_iris
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split

#算法（单一学习器）
from sklearn.neighbors import KNeighborsClassifier as KNNC
from sklearn.neighbors import KNeighborsRegressor as KNNR
from sklearn.tree import DecisionTreeRegressor as DTR
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.linear_model import LinearRegression as LR
from sklearn.linear_model import LogisticRegression as LogiR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.ensemble import GradientBoostingClassifier as GBC
from sklearn.naive_bayes import GaussianNB
import xgboost as xgb

#融合模型
from sklearn.ensemble import StackingClassifier

data = load_digits()
X = data.data
y = data.target

X.shape

np.unique(y) #10分类

Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.2,random_state=1412)

• 定义交叉验证函数

def fusion_estimators(clf):
    """
    对融合模型做交叉验证，对融合模型的表现进行评估
    """
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    results = cross_validate(clf,Xtrain,Ytrain
                             ,cv = cv
                             ,scoring = "accuracy"
                             ,n_jobs = -1
                             ,return_train_score = True
                             ,verbose=False)
    test = clf.fit(Xtrain,Ytrain).score(Xtest,Ytest)
    print("train_score:{}".format(results["train_score"].mean())
          ,"\n cv_mean:{}".format(results["test_score"].mean())
          ,"\n test_score:{}".format(test)
         )

def individual_estimators(estimators):
    """
    对模型融合中每个评估器做交叉验证，对单一评估器的表现进行评估
    """
    for estimator in estimators:
        cv = KFold(n_splits=5,shuffle=True,random_state=1412)
        results = cross_validate(estimator[1],Xtrain,Ytrain
                             ,cv = cv
                             ,scoring = "accuracy"
                             ,n_jobs = -1
                             ,return_train_score = True
                             ,verbose=False)
        test = estimator[1].fit(Xtrain,Ytrain).score(Xtest,Ytest)
        print(estimator[0]
          ,"\n train_score:{}".format(results["train_score"].mean())
          ,"\n cv_mean:{}".format(results["test_score"].mean())
          ,"\n test_score:{}".format(test)
          ,"\n")

• 个体学习器与元学习器的定义

我们之前在讲解Voting投票法的时候已经对如何定义个体学习器做出了详细的解释，也做了很多努力找出下面的7个模型。在这里，我们就沿用Voting当中选出的7个模型：

#逻辑回归没有增加多样性的选项
clf1 = LogiR(max_iter = 3000, C=0.1, random_state=1412,n_jobs=8)
#增加特征多样性与样本多样性
clf2 = RFC(n_estimators= 100,max_features="sqrt",max_samples=0.9, random_state=1412,n_jobs=8)
#特征多样性，稍微上调特征数量
clf3 = GBC(n_estimators= 100,max_features=16,random_state=1412) 

#增加算法多样性，新增决策树与KNN
clf4 = DTC(max_depth=8,random_state=1412)
clf5 = KNNC(n_neighbors=10,n_jobs=8)
clf6 = GaussianNB()

#新增随机多样性，相同的算法更换随机数种子
clf7 = RFC(n_estimators= 100,max_features="sqrt",max_samples=0.9, random_state=4869,n_jobs=8)
clf8 = GBC(n_estimators= 100,max_features=16,random_state=4869)

estimators = [("Logistic Regression",clf1), ("RandomForest", clf2)
              , ("GBDT",clf3), ("Decision Tree", clf4), ("KNN",clf5)
              #, ("Bayes",clf6)
              , ("RandomForest2", clf7), ("GBDT2", clf8)
             ]

• 导入sklearn进行建模

#选择单个评估器中分数最高的随机森林作为元学习器
#也可以尝试其他更简单的学习器
final_estimator = RFC(n_estimators=100
                      , min_impurity_decrease=0.0025
                      , random_state= 420, n_jobs=8)
clf = StackingClassifier(estimators=estimators #level0的7个体学习器
                         ,final_estimator=final_estimator #level 1的元学习器
                         ,n_jobs=8)

没有调过拟合之前：也就是没有加min_impurity_decrease=0.0025

fusion_estimators(clf) #没有过拟合限制
""
train_score:1.0
 cv_mean:0.9812112853271389
 test_score:0.9861111111111112
""

加上过拟合之后

fusion_estimators(clf) #精调过拟合
""
train_score:1.0
 cv_mean:0.9812185443283005
 test_score:0.9888888888888889
""

	benchmark	投票法	堆叠法
5折交叉验证	0.9666	0.9833	0.9812(↓)
测试集结果	0.9527	0.9889	0.9889(-)

可以看到，stacking在测试集上的分数与投票法Voting持平，但在5折交叉验证分数上却没有投票法高。这可能是由于现在我们训练的数据较为简单，但数据学习难度较大时，stacking的优势就会慢慢显现出来。当然，我们现在使用的元学习器几乎是默认参数，我们可以针对元学习器使用贝叶斯优化进行精妙的调参，然后再进行对比，堆叠法的效果可能超越投票法。

3 元学习器的特征矩阵

3.1 元学习器特征矩阵的2个问题

在Stacking过程中，个体学习器会原始数据上训练、预测，再把预测结果排布成新特征矩阵，放入元学习器进行学习。其中，个体学习器的预测结果、即元学习器需要训练的矩阵一般如下排布：

	学习器1	学习器2	...	学习器n
样本1	xxx	xxx	...	xxx
样本2	xxx	xxx	...	xxx
样本3	xxx	xxx	...	xxx
...	...	...	...	...
样本m	xxx	xxx	...	xxx

根据我们对机器学习以及模型融合的理解，不难发现以下两个问题：

• 首先，元学习器的特征矩阵中的特征一定很少

1个个体学习器只能输出1组预测结果，我们对这些预测结果进行排列，新特征矩阵中的特征数就等于个体学习器的个数。一般融合模型中个体学习器最多有20-30个，也就是说元学习器的特征矩阵中最多也就20-30个特征。这个特征量对于工业、竞赛中的机器学习算法来说是远远不够的。

• 其次，元学习器的特征矩阵中样本量也不太多

个体学习器的职责是找到原始数据与标签之间的假设，为了验证这个假设是否准确，我们需要查看的是个体学习器的泛化能力。只有当个体学习器的泛化能力较强时，我们才能安心的将个体学习器输出的预测结果放入元学习器中进行融合。

然而。在我们训练stacking模型时，我们一定是将原始数据集分为训练集、验证集和测试集三部分——

其中测试集是用于检测整个融合模型的效果的，因此在训练过程中不能使用。

而训练集用于训练个体学习器，属于已经完全透露给个体学习器的内容，如果在训练集上进行预测，那预测结果是“偏高”的、无法代表个体学习器的泛化能力。

因此最后剩下能够用来预测、还能代表个体学习器真实学习水平的，就只剩下很小的验证集了。一般验证集最多只占整个数据集的30%-40%，这意味着元学习器所使用的特征矩阵里的样本量最多也就是原始数据的40%。

无怪在行业惯例当中，元学习器需要是一个复杂度较低的算法，因为元学习器的特征矩阵在特征量、样本量上都远远小于工业机器学习所要求的标准。为了解决这两个问题，在Stacking方法当中存在多种解决方案，而这些解决方案可以通过sklearn中的stacking类实现。

class sklearn.ensemble.StackingClassifier(estimators, final_estimator=None, *, cv=None, stack_method='auto', n_jobs=None, passthrough=False, verbose=0)

class sklearn.ensemble.StackingRegressor(estimators, final_estimator=None, *, cv=None, n_jobs=None, passthrough=False, verbose=0)

参数	说明
estimators	个体评估器的列表。在sklearn中，只使用单一评估器作为个体评估器时， 模型可以运行，但效果往往不太好。
final_estimator	元学习器，只能有一个评估器。当融合模型执行分类任务时，元学习器一定是分类算法， 当融合模型执行回归任务时，元学习器一定是回归算法。
cv	用于指定交叉验证的具体类型、折数等细节。 可以执行简单的K折交叉验证，也可以输入sklearn中交叉验证类。
stack_method	只有分类器才有的参数，表示个体学习器输出的具体测试结果。
passthrough	在训练元学习器时，是否加入原始数据作为特征矩阵。
n_jobs, verbose	线程数与监控参数。

3.2 样本量太少的解决方案：交叉验证

• 参数cv，在stacking中执行交叉验证
  
  在stacking方法被提出的原始论文当中，原作者自然也意识到了元学习器的特征矩阵样本量太少这个问题，因此提出了在stacking流程内部使用交叉验证来扩充元学习器特征矩阵的想法，即在内部对每个个体学习器做交叉验证，但并不用这个交叉验证的结果来验证泛化能力，而是直接把交叉验证当成了生产数据的工具。

具体的来看，在stacking过程中，我们是这样执行交叉验证的——

对任意个体学习器来说，假设我们执行5折交叉验证，我们会将训练数据分成5份，并按照4份训练、1份验证的方式总共建立5个模型，训练5次：



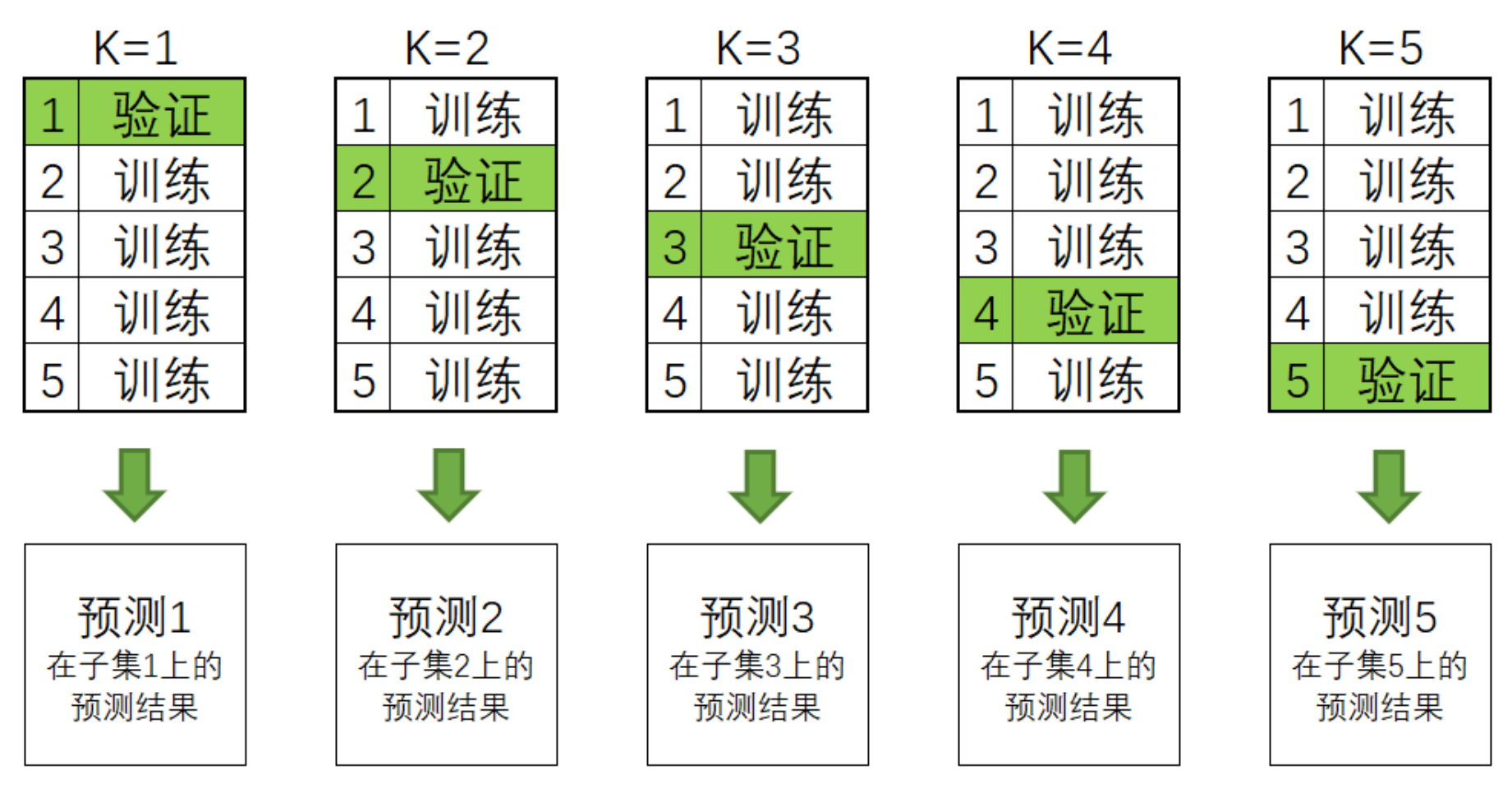
在交叉验证过程中，每次验证集中的数据都是没有被放入模型进行训练的，因此这些验证集上的预测结果都可以衡量模型的泛化能力。

一般来说，交叉验证的最终输出是5个验证集上的分数，但计算分数之前我们一定是在5个验证集上分别进行预测，并输出了结果。所以我们可以在交叉验证中建立5个模型，轮流得到5个模型输出的预测结果，而这5个预测结果刚好对应全数据集中分割的5个子集。这是说，我们完成交叉验证的同时，也对原始数据中全部的数据完成了预测。现在，只要将5个子集的预测结果纵向堆叠，就可以得到一个和原始数据中的样本一一对应的预测结果。这种纵向堆叠正像我们在海滩上堆石子(stacking)一样，这也是“堆叠法”这个名字的由来。



用这样的方法来进行预测，可以让任意个体学习器输出的预测值数量 = 样本量，如此，元学习器的特征矩阵的行数也就等于原始数据的样本量了：

	学习器1	学习器2	...	学习器n
样本1	xxx	xxx	...	xxx
样本2	xxx	xxx	...	xxx
样本3	xxx	xxx	...	xxx
...	...	...	...	...
样本m	xxx	xxx	...	xxx

在stacking过程中，这个交叉验证流程是一定会发生的，不属于我们可以人为干涉的范畴。不过，我们可以使用参数cv来决定具体要使用怎样的交叉验证，包括具体使用几折验证，是否考虑分类标签的分布等等。具体来说，参数cv中可以输入：

输入None，默认使用5折交叉验证

输入sklearn中任意交叉验证对象

输入任意整数，表示在Stratified K折验证中的折数。Stratified K折验证是会考虑标签中每个类别占比的交叉验证，如果选择Stratified K折交叉验证，那每次训练时交叉验证会保证原始标签中的类别比例 = 训练标签的类别比例 = 验证标签的类别比例。



现在你知道Stacking是如何处理元学习器的特征矩阵样本太少的问题了。需要再次强调的是，内部交叉验证的并不是在验证泛化能力，而是一个生产数据的工具，因此交叉验证本身没有太多可以调整的地方。唯一值得一提的是，当交叉验证的折数较大时，模型的抗体过拟合能力会上升、同时学习能力会略有下降。当交叉验证的折数很小时，模型更容易过拟合。但如果数据量足够大，那使用过多的交叉验证折数并不会带来好处，反而只会让训练时间增加而已：

estimators = [("Logistic Regression",clf1), ("RandomForest", clf2)
              , ("GBDT",clf3), ("Decision Tree", clf4), ("KNN",clf5)
              #, ("Bayes",clf6)
              , ("RandomForest2", clf7), ("GBDT2", clf8)
             ]
final_estimator = RFC(n_estimators=100
                      , min_impurity_decrease=0.0025
                      , random_state= 420, n_jobs=8)

def cvtest(cv):
    clf = StackingClassifier(estimators=estimators
                         ,final_estimator=final_estimator
                         , cv = cv
                         , n_jobs=8)
    start = time.time()
    clf.fit(Xtrain,Ytrain)
    print((time.time() - start)) #消耗时间
    print(clf.score(Xtrain,Ytrain)) #训练集上的结果
    print(clf.score(Xtest,Ytest)) #测试集上的结果

cvtest(2) #非常少的验证次数
""
3.8339908123016357
1.0
0.9861111111111112
""

cvtest(10) #普通的验证次数
""
13.57864761352539
1.0
0.9833333333333333
""

cvtest(30) #很大的验证次数
""
39.74843621253967
1.0
0.9833333333333333
""

可以看到，随着cv中折数的上升，训练时间一定会上升，但是模型的表现却不一定。因此，选择5~10折交叉验证即可。同时，由于stacking当中自带交叉验证，又有元学习器这个算法，因此堆叠法的运行速度是比投票法、均值法缓慢很多的，这是stacking堆叠法不太人性化的地方。

3.3 特征太少的解决方案

• 参数stack_method，更换个体学习器输出的结果类型

对于分类stacking来说，如果特征量太少，我们可以更换个体学习器输出的结果类型。具体来说，如果个体学习器输出的是具体类别（如[0,1,2]），那1个个体学习器的确只能输出一列预测结果。但如果把输出的结果类型更换成概率值、置信度等内容，输出结果的结构一下就可以从一列拓展到多列。

如果这个行为由参数stack_method控制，这是只有StackingClassifier才拥有的参数，它控制个体分类器具体的输出。stack_method里面可以输入四种字符串："auto", "predict_proba", "decision_function", "predict"，除了"auto"之外其他三个都是sklearn常见的接口。

clf = LogiR(max_iter=3000, random_state=1412)

clf = clf.fit(Xtrain,Ytrain)

#predict_proba：输出概率值
clf.predict_proba(Xtrain)

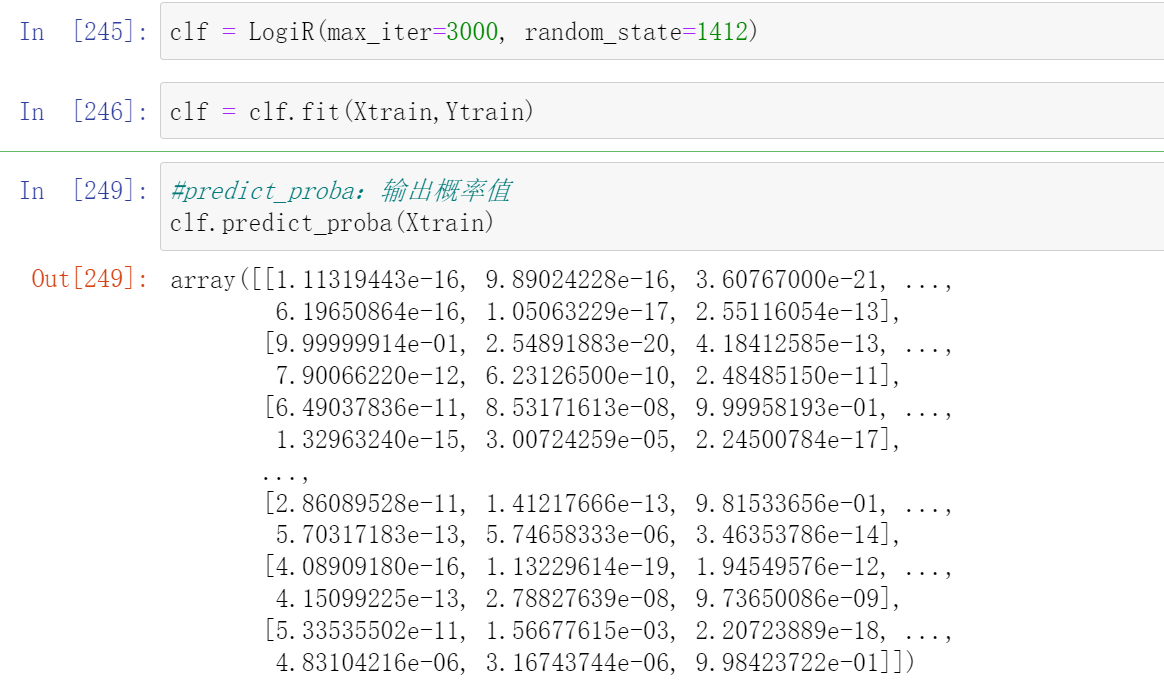
#decision_function：每个样本点到分类超平面的距离，可以衡量置信度
#对于无法输出概率的算法，如SVM，我们通常使用decision_function来输出置信度
clf.decision_function(Xtrain)

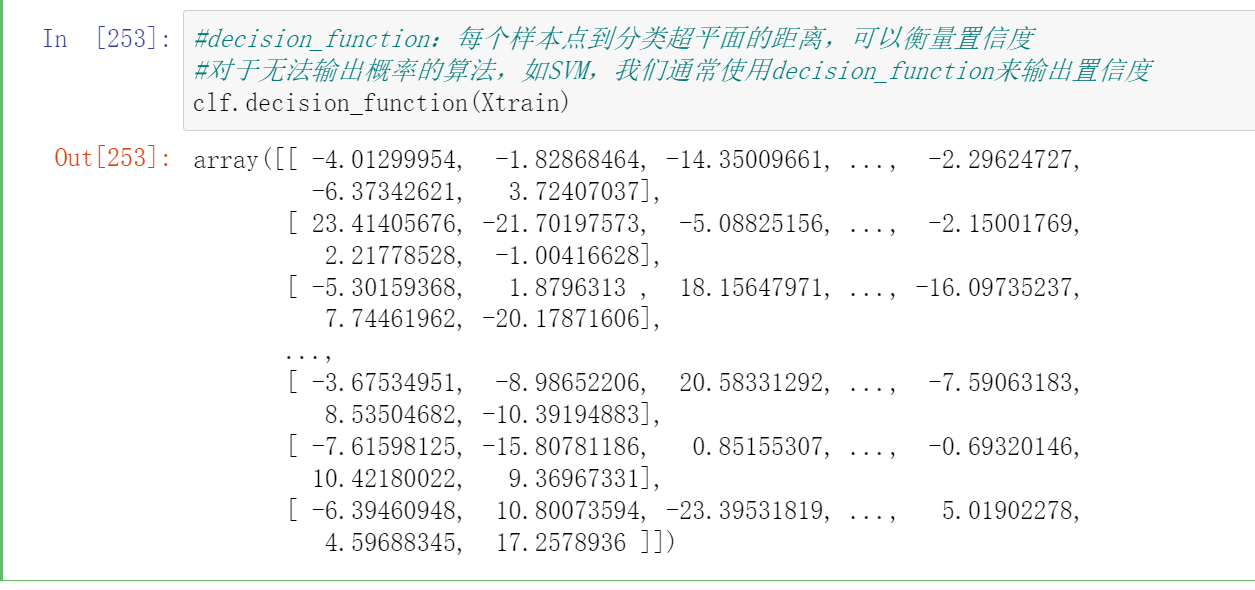
#predict：输出具体的预测标签
clf.predict(Xtrain)

对参数stack_method有：

输入"auto"，sklearn会在每个个体学习器上按照"predict_proba", "decision_function", "predict"的顺序，分别尝试学习器可以使用哪个接口进行输出。即，如果一个算法可以使用predict_proba接口，那就不再尝试后面两个接口，如果无法使用predict_proba，就尝试能否使用decision_function。

输入三大接口中的任意一个接口名，则默认全部个体学习器都按照这一接口进行输出。然而，如果遇见某个算法无法按照选定的接口进行输出，stacking就会报错。

因此，我们一般都默认让stack_method保持为"auto"。从上面的我们在逻辑回归上尝试的三个接口结果来看，很明显，当我们把输出的结果类型更换成概率值、置信度等内容，输出结果的结构一下就可以从一列拓展到多列。

• predict_proba

对二分类，输出样本的真实标签1的概率，一列

对n分类，输出样本的真实标签为[0,1,2,3...n]的概率，一共n列

• decision_function

对二分类，输出样本的真实标签为1的置信度，一列

对n分类，输出样本的真实标签为[0,1,2,3...n]的置信度，一共n列

• predict

对任意分类形式，输出算法在样本上的预测标签，一列

在实践当中，我们会发现输出概率/置信度的效果比直接输出预测标签的效果好很多，既可以向元学习器提供更多的特征、还可以向元学习器提供个体学习器的置信度。我们在投票法中发现使用概率的“软投票”比使用标签类被的“硬投票”更有效，也是因为考虑了置信度。

• 参数passthrough，将原始特征矩阵加入新特征矩阵

对于分类算法，我们可以使用stack_method，但是对于回归类算法，我们没有这么多可以选择的接口。回归类算法的输出永远就只有一列连续值，因而我们可以考虑将原始特征矩阵加入个体学习器的预测值，构成新特征矩阵。这样的话，元学习器所使用的特征也不会过于少了。当然，这个操作有较高的过拟合风险，因此当特征过于少、且stacking算法的效果的确不太好的时候，我们才会考虑这个方案。

控制是否将原始数据加入特征矩阵的参数是passthrough，我们可以在该参数中输入布尔值。当设置为False时，表示不将原始特征矩阵加入个体学习器的预测值，设置为True时，则将原始特征矩阵加入个体学习器的预测值、构成大特征矩阵。

• 接口transform与属性stack_method_

estimators = [("Logistic Regression",clf1), ("RandomForest", clf2)
              , ("GBDT",clf3), ("Decision Tree", clf4), ("KNN",clf5)
              #, ("Bayes",clf6)
              , ("RandomForest2", clf7), ("GBDT2", clf8)
             ]

final_estimator = RFC(n_estimators=100
                      , min_impurity_decrease=0.0025
                      , random_state= 420, n_jobs=8)
clf = StackingClassifier(estimators=estimators
                         ,final_estimator=final_estimator
                         ,stack_method = "auto"
                         ,n_jobs=8)

clf = clf.fit(Xtrain,Ytrain)

当我们训练完毕stacking算法后，可以使用接口transform来查看当前元学习器所使用的训练特征矩阵的结构：

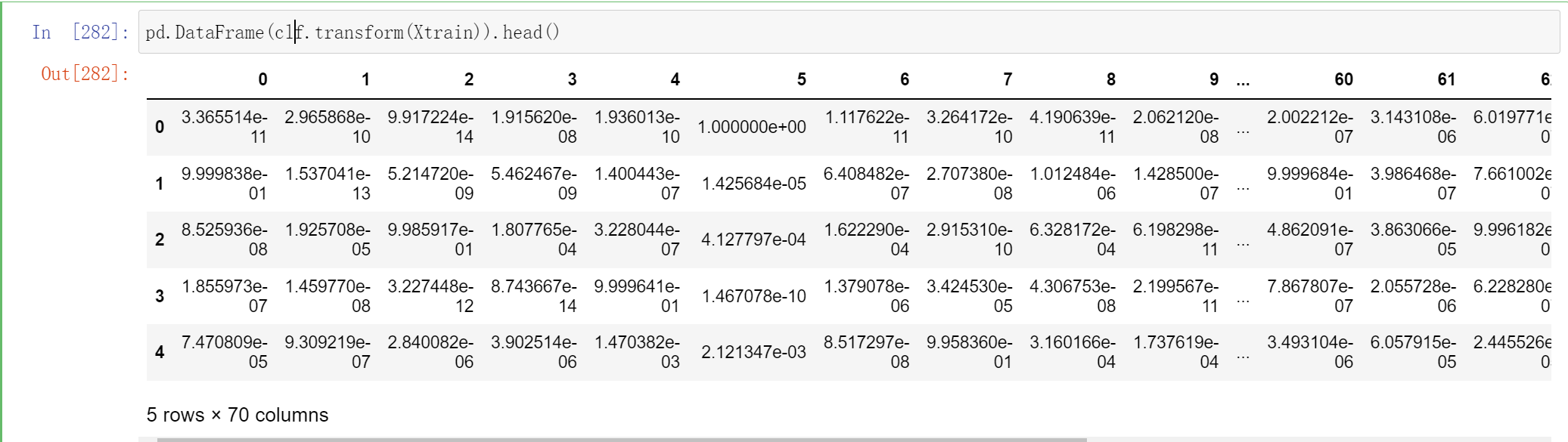
clf.transform(Xtrain).shape
# (1437, 70)

这个70 代表这个一共有7个个体学习器，每个个体学习器都有10个概率输出

如之前所说，这个特征矩阵的行数就等于训练的样本量：

Xtrain.shape[0]
# 1437

不过你能判断为什么这里有70列吗？因为我们有7个个体学习器，而现在数据是10分类的数据，因此每个个体学习器都输出了类别[0,1,2,3,4,5,6,7,8,9]所对应的概率，因此总共产出了70列数据：

pd.DataFrame(clf.transform(Xtrain)).head()

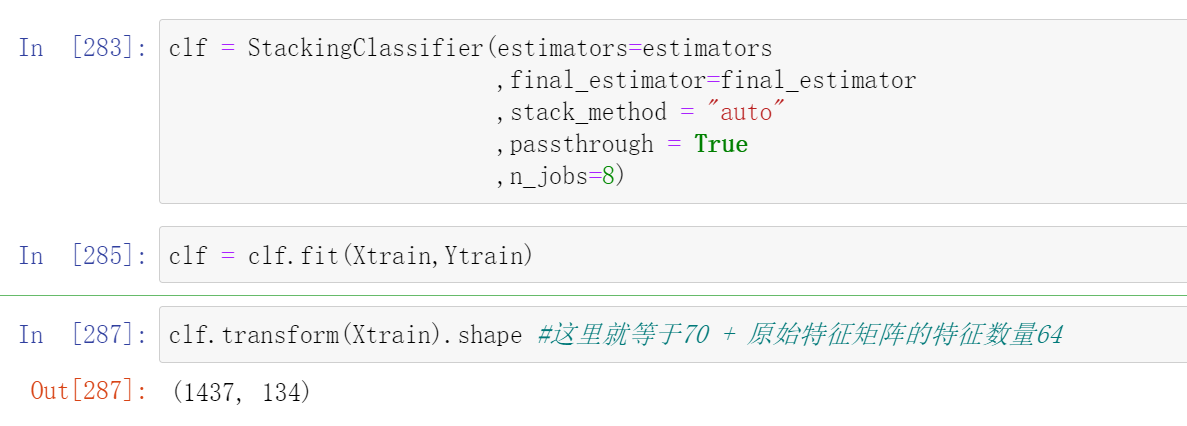
如果加入参数passthrough，特征矩阵的特征量会变得更大：

clf = StackingClassifier(estimators=estimators
                         ,final_estimator=final_estimator
                         ,stack_method = "auto"
                         ,passthrough = True
                         ,n_jobs=8)

clf = clf.fit(Xtrain,Ytrain)

clf.transform(Xtrain).shape #这里就等于70 + 原始特征矩阵的特征数量64
# (1437, 134)

使用属性stack_method_，我们可以查看现在每个个体学习器都使用了什么接口做为预测输出：

clf.stack_method_

['predict_proba',

'predict_proba',

'predict_proba',

'predict_proba',

'predict_proba',

'predict_proba',

'predict_proba']

不难发现，7个个体学习器都使用了predict_proba的概率接口进行输出，这与我们选择的算法都是可以输出概率的算法有很大的关系

4 Stacking融合的训练/测试流程

现在我们已经知道了stacking算法中所有关于训练的信息，我们可以梳理出如下训练流程：

• stacking的训练

1. 将数据分割为训练集、测试集，其中训练集上的样本为\(M_{train}\)，测试集上的样本量为\(M_{test}\)
2. 将训练集输入level 0的个体学习器，分别在每个个体学习器上进行交叉验证。在每个个体学习器上，将所有交叉验证的验证结果纵向堆叠形成预测结果。假设预测结果为概率值，当融合模型执行回归或二分类任务时，该预测结果的结构为\((M_{train},1)\)，当融合模型执行K分类任务时(K>2)，该预测结果的结构为\((M_{train},K)\)
3. 将所有个体学习器的预测结果横向拼接，形成新特征矩阵。假设共有N个个体学习器，则新特征矩阵的结构为\((M_{train}, N)\)。如果是输出多分类的概率，那最终得出的新特征矩阵的结构为\((M_{train}, N*K)\)
4. 将新特征矩阵放入元学习器进行训练。

不难发现，虽然训练的流程看起来比较流畅，但是测试却不知道从何做起，因为：

• 最终输出预测结果的是元学习器，因此直觉上来说测试数据集或许应该被输入到元学习器当中。然而，元学习器是使用新特征矩阵进行预测的，新特征矩阵的结构与规律都与原始数据不同，所以元学习器根本不可能接受从原始数据中分割出来的测试数据。因此正确的做法应该是让测试集输入level 0的个体学习器。

• 然而，这又存在问题了：level 0的个体学习器们在训练过程中做的是交叉验证，而交叉验证只会输出验证结果，不会留下被训练的模型。因此在level 0中没有可以用于预测的、已经训练完毕的模型。

为了解决这个矛盾在我们的训练流程中，存在着隐藏的步骤：

• stacking的训练

1. 将数据分割为训练集、测试集，其中训练集上的样本为\(M_{train}\)，测试集上的样本量为\(M_{test}\)
2. 将训练集输入level 0的个体学习器，分别在每个个体学习器上进行交叉验证。在每个个体学习器上，将所有交叉验证的验证结果纵向堆叠形成预测结果。假设预测结果为概率值，当融合模型执行回归或二分类任务时，该预测结果的结构为\((M_{train},1)\)，当融合模型执行K分类任务时(K>2)，该预测结果的结构为\((M_{train},K)\)
3. 隐藏步骤：使用全部训练数据对所有个体学习器进行训练，为测试做好准备。
4. 将所有个体学习器的预测结果横向拼接，形成新特征矩阵。假设共有N个个体学习器，则新特征矩阵的结构为\((M_{train}, N)\).
5. 将新特征矩阵放入元学习器进行训练。

• stacking的测试

1. 将测试集输入level0的个体学习器，分别在每个个体学习器上预测出相应结果。假设测试结果为概率值，当融合模型执行回归或二分类任务时，该测试结果的结构为\((M_{test},1)\)，当融合模型执行K分类任务时(K>2)，该测试结果的结构为\((M_{test},K)\)
2. 将所有个体学习器的预测结果横向拼接为新特征矩阵。假设共有N个个体学习器，则新特征矩阵的结构为\((M_{test}, N)\).
3. 将新特征矩阵放入元学习器进行预测。

因此在stacking中，不仅要对个体学习器完成全部交叉验证，还需要在交叉验证结束后，重新使用训练数据来训练所有的模型。无怪Stacking融合的复杂度较高、并且运行缓慢了。

到现在，我们已经讲解完毕投票法和堆叠法了。在sklearn中，我们讲解了下面4个类：

融合方法	类
投票法	ensemble.VotingClassifier
平均法	ensemble.VotingRegressor
堆叠法分类	ensemble.StackingClassifier
堆叠法回归	ensemble.StackingRegressor

虽然这些类是模型融合方法，但我们可以像使用任意单一算法类一样任意地使用这些方法——我们可以很轻松地对这些类执行手动调参、交叉验证、网格搜索、贝叶斯优化、管道打包等操作，而无需担心代码的兼容问题。但需要注意的是，sklearn中的融合工具只支持sklearn中的评估器，不支持xgb、lgbm的原生代码。因此，如果我们想要对原生代码下的模型进行融合，必须自己手写融合过程。

二 改进后的堆叠法：Blending

1 Blending的基本思想与流程

Blending融合是在Stacking融合的基础上改进过后的算法。在之前的课程中我们提到，堆叠法stacking在level1上使用算法，这可以令融合本身向着损失函数最小化的方向进行，同时stacking使用自带的内部交叉验证来生成数据，可以深度使用训练数据，让模型整体的效果更好。但在这些操作的背后，存在两个巨大的问题：

• stacking融合需要巨大的计算量，需要的时间和算力成本较高，以及

• stacking融合在数据和算法上都过于复杂，因此融合模型过拟合的可能性太高。

针对stacking存在的这两个问题，竞赛冠军队们持续探索，并且在实践过程中创造了多种改进的stacking方法。今天，多种stacking方法中较为有效的方法之一就是著名的Blending方法。Blending直译为“混合”，但它的核心思路其实与Stacking完全一致：使用两层算法串联，level0上存在多个强学习器，level1上有且只有一个元学习器，且level0上的强学习器负责拟合数据与真实标签之间的关系、并输出预测结果、组成新的特征矩阵，然后让level1上的元学习器在新的特征矩阵上学习并预测。

然而，与stacking不同的是，为了降低计算量、降低融合模型过拟合风险，Blending取消了K折交叉验证、并且大大地降低了元学习器所需要训练的数据量，其具体流程如下：

• blending的训练

1. 将数据分割为训练集、验证集与测试集，其中训练集上的样本为\(M_{train}\)，验证集上的样本为\(M_v\)，测试集上的样本量为\(M_{test}\)
2. 将训练集输入level 0的个体学习器，分别在每个个体学习器上训练。训练完毕后，在验证集上进行验证，输出验证集上的预测结果。假设预测结果为概率值，当融合模型执行回归或二分类任务时，该预测结果的结构为\((M_v,1)\)，当融合模型执行K分类任务时(K>2)，该预测结果的结构为\((M_v,K)\)。此时此刻，所有个体学习器都被训练完毕了。
3. 将所有个体学习器的验证结果横向拼接，形成新特征矩阵。假设共有N个个体学习器，则新特征矩阵的结构为\((M_v, N)\)。
4. 将新特征矩阵放入元学习器进行训练。

• blending的测试

1. 将测试集输入level0的个体学习器，分别在每个个体学习器上预测出相应结果。假设测试结果为概率值，当融合模型执行回归或二分类任务时，该测试结果的结构为\((M_{test},1)\)，当融合模型执行K分类任务时(K>2)，该测试结果的结构为\((M_{test},K)\)
2. 将所有个体学习器的预测结果横向拼接为新特征矩阵。假设共有N个个体学习器，则新特征矩阵的结构为\((M_{test}, N)\).
3. 将新特征矩阵放入元学习器进行预
   
   测。

2 手动实现Blending算法

def BlendingClassifier(X,y,estimators,final_estimator,test_size=0.2,vali_size=0.4):
    """
    该函数用于实现Blending分类融合
    X,y：整体数据集，会被分割为训练集、测试集、验证集三部分
    estimators: level0的个体学习器，输入格式形如sklearn中要求的[(名字，算法)，(名字，算法)...]
    final_estimator：元学习器
    test_size：测试集占全数据集的比例
    vali_size：验证集站全数据集的比例

    """

    #第一步，分割数据集
    #1.分测试集
    #2.分训练和验证集，验证集占完整数据集的比例为0.4，因此占排除测试集之后的比例为0.4/(1-0.2)
    X_,Xtest,y_,Ytest = train_test_split(X,y,test_size=test_size,random_state=1412)
    Xtrain,Xvali,Ytrain,Yvali = train_test_split(X_,y_,test_size=vali_size/(1-test_size),random_state=1412)

    #训练
    #建立空dataframe用于保存个体学习器上的验证结果，即用于生成新特征矩阵
    #新建空列表用于保存训练完毕的个体学习器，以便在测试中使用
    NewX_vali = pd.DataFrame()
    trained_estimators = []
    #循环、训练每个个体学习器、并收集个体学习器在验证集上输出的概率
    for clf_id, clf in estimators:
        clf = clf.fit(Xtrain,Ytrain)
        val_predictions = pd.DataFrame(clf.predict_proba(Xvali))
        #保存结果，在循环中逐渐构筑新特征矩阵
        NewX_vali = pd.concat([NewX_vali,val_predictions],axis=1)
        trained_estimators.append((clf_id,clf))
    #元学习器在新特征矩阵上训练、并输出训练分数
    final_estimator = final_estimator.fit(NewX_vali,Yvali)
    train_score = final_estimator.score(NewX_vali,Yvali)

    #测试
    #建立空dataframe用于保存个体学习器上的预测结果，即用于生成新特征矩阵
    NewX_test = pd.DataFrame()
    #循环，在每个训练完毕的个体学习器上进行预测，并收集每个个体学习器上输出的概率
    for clf_id,clf in trained_estimators:
        test_prediction = pd.DataFrame(clf.predict_proba(Xtest))
        #保存结果，在循环中逐渐构筑特征矩阵
        NewX_test = pd.concat([NewX_test,test_prediction],axis=1)
    #元学习器在新特征矩阵上测试、并输出测试分数
    test_score = final_estimator.score(NewX_test,Ytest)

    #打印训练分数与测试分数
    print(train_score,test_score)

#逻辑回归没有增加多样性的选项
clf1 = LogiR(max_iter = 3000, C=0.1, random_state=1412,n_jobs=8)
#增加特征多样性与样本多样性
clf2 = RFC(n_estimators= 100,max_features="sqrt",max_samples=0.9, random_state=1412,n_jobs=8)
#特征多样性，稍微上调特征数量
clf3 = GBC(n_estimators= 100,max_features=16,random_state=1412) 

#增加算法多样性，新增决策树与KNN
clf4 = DTC(max_depth=8,random_state=1412)
clf5 = KNNC(n_neighbors=10,n_jobs=8)
clf6 = GaussianNB()

#新增随机多样性，相同的算法更换随机数种子
clf7 = RFC(n_estimators= 100,max_features="sqrt",max_samples=0.9, random_state=4869,n_jobs=8)
clf8 = GBC(n_estimators= 100,max_features=16,random_state=4869)

estimators = [("Logistic Regression",clf1), ("RandomForest", clf2)
              , ("GBDT",clf3), ("Decision Tree", clf4), ("KNN",clf5)
              #, ("Bayes",clf6)
              #, ("RandomForest2", clf7), ("GBDT2", clf8)
             ]

final_estimator = RFC(n_estimators= 100
                      #, max_depth = 8
                      , min_impurity_decrease=0.0025
                      , random_state= 420, n_jobs=8)

#很明显，过拟合程度比Stacking要轻，但是测试集的表现没有stacking强
BlendingClassifier(X,y,estimators,final_estimator)

#验证比例越大，模型学习能力越弱 - 注意验证集比例上限0.8，因为有0.2是测试数据
BlendingClassifier(X,y,estimators,final_estimator,vali_size=0.7)

#blending的运行速度比stacking快了不止一个档次……
BlendingClassifier(X,y,estimators,final_estimator,vali_size=0.1)
""
1.0 0.9833333333333333
""

	benchmark	投票法	Stacking	Blending
5折交叉验证	0.9666	0.9833	0.9812(↓)	-
测试集结果	0.9527	0.9889	0.9889(-)	0.9833(↓)

从结果来看，投票法表现最稳定和优异，这与我们选择的数据集是较为简单的数据集有关，同时投票法也是我们调整最多、最到位的算法。在大型数据集上运行时，stacking和blending会展现出更多的优势。到这里我们的blending就讲解完毕了，在《2022机器学习实战》正式课程当中，我们将会更详细地讲解Blending在xgboost等复杂算法上的应用。