大模型高效微调-LoRA原理详解和训练过程深入分析

博客首发于我的知乎，详见：https://zhuanlan.zhihu.com/p/702629428

一、LoRA原理

LoRA(Low-Rank Adaptation of LLMs)，即LLMs的低秩适应，是参数高效微调最常用的方法。

LoRA的本质就是用更少的训练参数来近似LLM全参数微调所得的增量参数，从而达到使用更少显存占用的高效微调。

1.1 问题定义

LoRA与训练目标是解耦的，但本文设定就是语言模型建模。

以下将给出语言建模（可自然推广到序列建模）的基本符号定义，即最大化给定提示的条件概率（本质是极大似然估计）。

The maximization of conditional probabilities given a task-specific prompt

给定一个参数为\(\mathbf{\Phi}\)预训练的自回归语言模型$ P_{\Phi}(y|x)$。

\(x\)为输入，\(y\)为输出

note: 为与原文符号一致，下文\(\mathbf{\Phi}\)、\(\mathbf{\Theta}\)、\(\mathbf{W}\)均表示模型参数

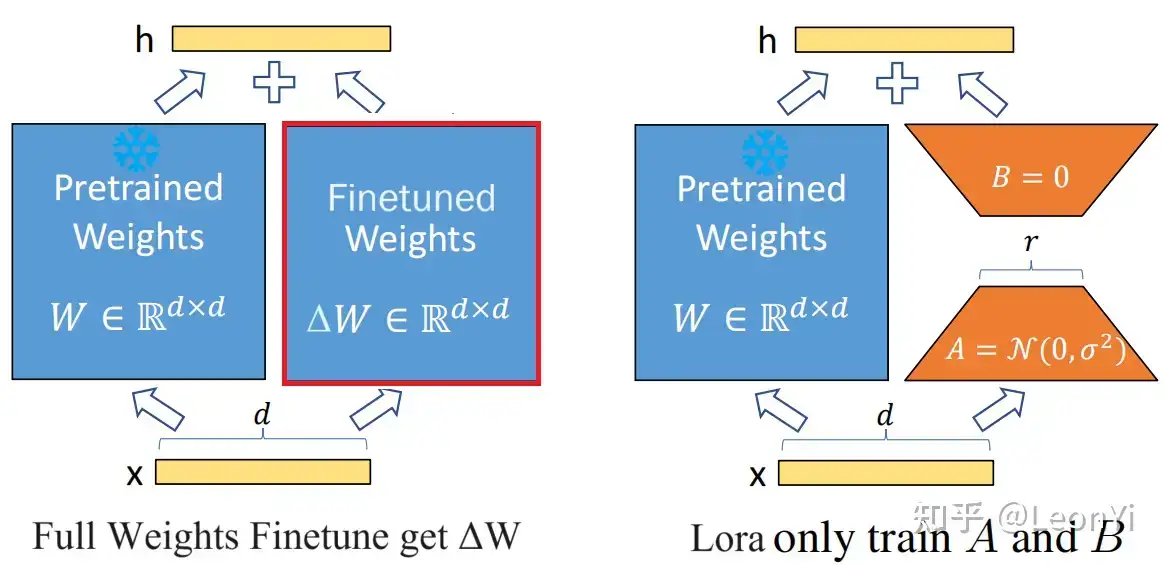
全参数微调

每次full fine-tuning训练，学一个 \(\Delta \mathbf{\Phi}\)，\(|\Delta \mathbf{\Phi}|\) 参数量大hold不住

语言模型的条件概率分布建模目标

高效微调

$ \Delta \mathbf{\Phi}$ 是特定于下游任务的增量参数

LoRA将 $ \Delta \mathbf{\Phi}=\Delta \mathbf{\Phi}(\Theta)$ ，用参数量更少的$ \mathbf{\Theta}$来编码（低秩降维表示来近似）, \(|\mathbf{\Phi}| << | \mathbf{\Theta}|\)

LoRA训练目标

Transformer架构参数

Transformer层的输入和输出维度大小 \(d_{model}\)

\(\mathbf{W_q}\)、\(\mathbf{W_k}\)、\(\mathbf{W_v}\),和\(\mathbf{W_o}\)分别代表自注意力的query、key、value和output投影矩阵

\(\mathbf{W}\)或\(\mathbf{W}_0\)代表预训练的权重矩阵

\(∆\mathbf{W}\)是微调后得到的增量参数矩阵（训练后，优化算法在参数上的累计更新量）

\(r\)代表LoRA模块的秩

1.2 LoRA简介

LoRA的核心思想是，在冻结预训练模型权重后，将可训练的低秩分解矩阵注入到的Transformer架构的每一层中，从而大大减少了在下游任务上的可训练参数量。

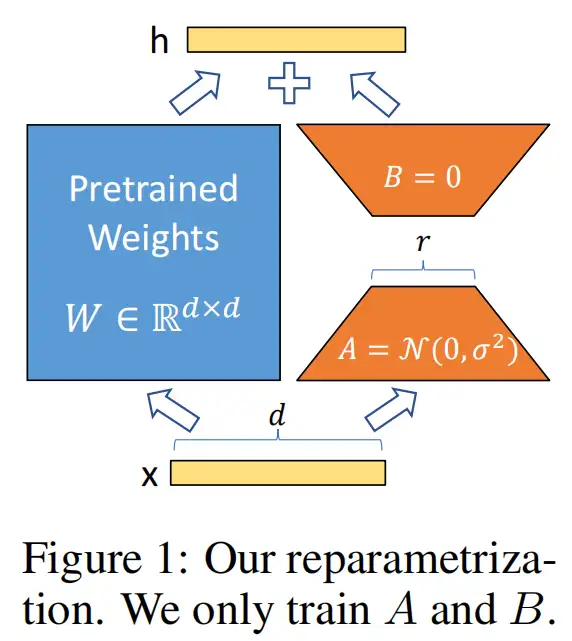
LoRA结构

We propose Low-Rank Adaptation(LoRA), which freezes the pre trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks.

在推理时，对于使用LoRA的模型来说，可直接将原预训练模型权重与训练好的LoRA权重合并，因此在推理时不存在额外开销。

1.3 为什么要LoRA

背景

通常，冻结预训练模型权重，再额外插入可训练的权重是常规做法，例如Adapter。可训练的权重学习的就是微调数据的知识。

但它们的问题在于，不仅额外增加了参数，而且还改变了模型结构。

这会导致模型训练、推理的计算成本和内存占用急剧增加，尤其在模型参数需在多GPU上分布式推理时（这越来越常见）。

推理性能比较

动机

深度网络由大量Dense层构成，这些参数矩阵通常是满秩的。

相关工作表明，When adapting to a specific task, 训练学到的过度参数化的模型实际上存在于一个较低的内在维度上（高维数据实际是在低维子空间中）

We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) which show that the learned over-parametrized models in fact reside on a low intrinsic dimension.

低秩矩阵

LoRA就假设LLM在下游任务上微调得到的增量参数矩阵\(\Delta \mathbf{W}\)是低秩的（肯定不是满秩），即存在冗余参数或高度相关的参数矩阵，但实际有效参数是更低维度的。

We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposed Low-Rank Adaptation (LoRA) approach.

LoRA遂设想，对全参数微调的增量参数矩阵\(\Delta \mathbf{W}\)进行低秩分解近似表示（即对参数做降维）。

PCA降维示意图，源于https://lightning.ai/pages/community/tutorial/lora-llm/

这样训练\(\Delta \mathbf{W}\)的低秩分解近似参数矩阵，效果上相比其他PEFT方法不会打什么折扣，而且还能在推理时不增加额外开销。

LoRA allows us to train some dense layers in a neural network indirectly by optimizing rank decomposition matrices of the dense layers’ change during adaptation instead, while keeping the pre-trained weights frozen

LoRA的大体思路就是这样，具体的矩阵分解也是靠微调过程学习的。

接下来，介绍LoRA的具体方案。

1.4 LoRA实现

LoRA就是低秩矩阵适应，在冻结原有LLM参数时，用参数量更小的矩阵进行低秩近似训练。

LoRA原理

对于预训练权重矩阵\(\mathbf{W}_{0} \in \mathbb{R}^{d \times d}\)，LoRa限制了其更新方式，即将全参微调的增量参数矩阵\(\Delta \mathbf{W}\)表示为两个参数量更小的矩阵$\mathbf{B} \(和\)\mathbf{A}$的低秩近似：

\[\mathbf{W}_{0} + \Delta \mathbf{W} = \mathbf{W}_{0}+ \mathbf{B}\mathbf{A}
\]

其中，\(\mathbf{B}\in \mathbb{R}^{d \times r}\)和\(\mathbf{A}\in \mathbb{R}^{r \times d}\)为LoRA低秩适应的权重矩阵，秩\(r\)远小于\(d\)。

此时，微调的参数量从原来\(\Delta \mathbf{W}\)的\(d*d\)，变成了\(\mathbf{B}\) 和 \(\mathbf{A}\)的\(2*r*d\)。可知，\(2*r*d << d*d\)（有\(2r << d\)）

给定输入\(\mathbf{x} \in \mathbb{R}^{d}\)，添加LoRA后的输出\(\mathbf{h} \in \mathbb{R}^{d}\)：

\[\mathbf{h} = (\mathbf{W}_{0} + \Delta \mathbf{W} ) \mathbf{x} = \mathbf{W}_{0}\mathbf{x} + \mathbf{B}\mathbf{A} \mathbf{x}
\]

这里，将\(\Delta \mathbf{h}=\mathbf{B}\mathbf{A} \mathbf{x}\)，便于后续求导计算。

在训练时，原始参数\(\mathbf{W}_{0}\)被冻结，意味着\(\mathbf{W}_{0}\)虽然会参与前向传播和反向传播，但是不会计算其对应梯度\(\frac{\partial L}{\partial \mathbf{W}_0}\)，更不会更新其参数。

在推理时，直接按上面的式子将\(\mathbf{B}\mathbf{A}\)合并到\(\mathbf{W}_{0}\)中，因此相比原始LLM不存在推理延时。

1.5 LoRA参数初始化

在开始训练时：

• 矩阵 \(\mathbf{B}\) 通过高斯函数初始化，\(b_i \sim N(0, {\sigma_b}^2)\)

• 矩阵 \(\mathbf{A}\) 为全零初始化，\(a_i = 0\)

这使得训练开始前，LoRA的旁路\(\mathbf{B}\mathbf{A}=0\)，那么微调就能从预训练权重\(\mathbf{W}_{0}\)开始。

这样就能和全参数微调时一样，能有相同的开始。

这个策略要求，至少\(\mathbf{B}\) 和 \(\mathbf{A}\)中有一个被初始化为全0项。

但如果，全被初始化为0，\(\mathbf{B}\) 和 \(\mathbf{A}\)就训不动了。因为，\(\mathbf{B}\) 和 \(\mathbf{A}\)全0时，处于鞍点，两个权重的梯度也全为0

（\(\mathbf{B}\) 的梯度 \(\frac{\partial L}{\partial \mathbf{B}}\)依赖\(\mathbf{A}\)，\(\mathbf{A}\) 的梯度\(\frac{\partial L}{\partial \mathbf{A}}\)依赖\(\mathbf{B}\)，如果仅一项为0训练是可以启动的）

1.6 LoRA权重系数\(\frac{\alpha}{r}\)

实际实现时，\(\Delta \mathbf{W} = \mathbf{B}\mathbf{A}\)会乘以系数\(\frac{\alpha}{r}\)与原始预训练权重合并\(\mathbf{W}_{0}\)，\(\alpha\)是一个超参：

\[\mathbf{h} = (\mathbf{W}_{0} + \frac{\alpha}{r} \Delta \mathbf{W})\mathbf{x}
\]

直观来看，系数\(\frac{\alpha}{r}\)决定了在下游任务上微调得到的LoRA低秩适应的权重矩阵\(\mathbf{B}\mathbf{A}\)占最终模型参数的比例。

给定一个或多个下游任务数据，进行LoRA微调：

• 系数\(\frac{\alpha}{r}\)越大，LoRA微调权重的影响就越大，在下游任务上越容易过拟合
• 系数\(\frac{\alpha}{r}\)越小，LoRA微调权重的影响就越小（微调的效果不明显，原始模型参数受到的影响也较少）

一般来说，在给定任务上LoRA微调，让\({\alpha}\)为\(r\)的2倍数。（太大学过头了，太小学不动。）

根据经验，LoRA训练大概很难注入新的知识，更多是修改LLM的指令尊随的能力，例如输出风格和格式。原始的LLM能力，是在预训练是获得的（取决于参数量、数据规模X数据质量）。

LoRA的秩\(r\)决定，LoRA的低秩近似矩阵的拟合能力，实际任务需要调参挑选合适的秩\(r\)维度。系数\(\frac{\alpha}{r}\)中\(\alpha\)决定新老权重的占比。

1.7 LoRA的秩\(r\)如何选择

和推荐系统中的评分矩阵分解、文本的非负矩阵分解，以及奇异值分解一样。LoRA的低秩分解近似矩阵\(\mathbf{B}\) 和 \(\mathbf{A}\)的秩\(r\)的大小，决定了其拟合能力。

理想的情况是找到一个秩\(r\)，使得LoRA的低秩近似结构\(\mathbf{B}\mathbf{A}\)能具备全参数微调的增量矩阵\(\Delta \mathbf{W}\) 的表达能力，能越接近越好。

秩\(r\)成为了LoRA的超参数，随着秩\(r\)维度的不断增加，参与训练的参数量也随之增加，LoRA的低秩适应能力将逐渐提高甚至过拟合。

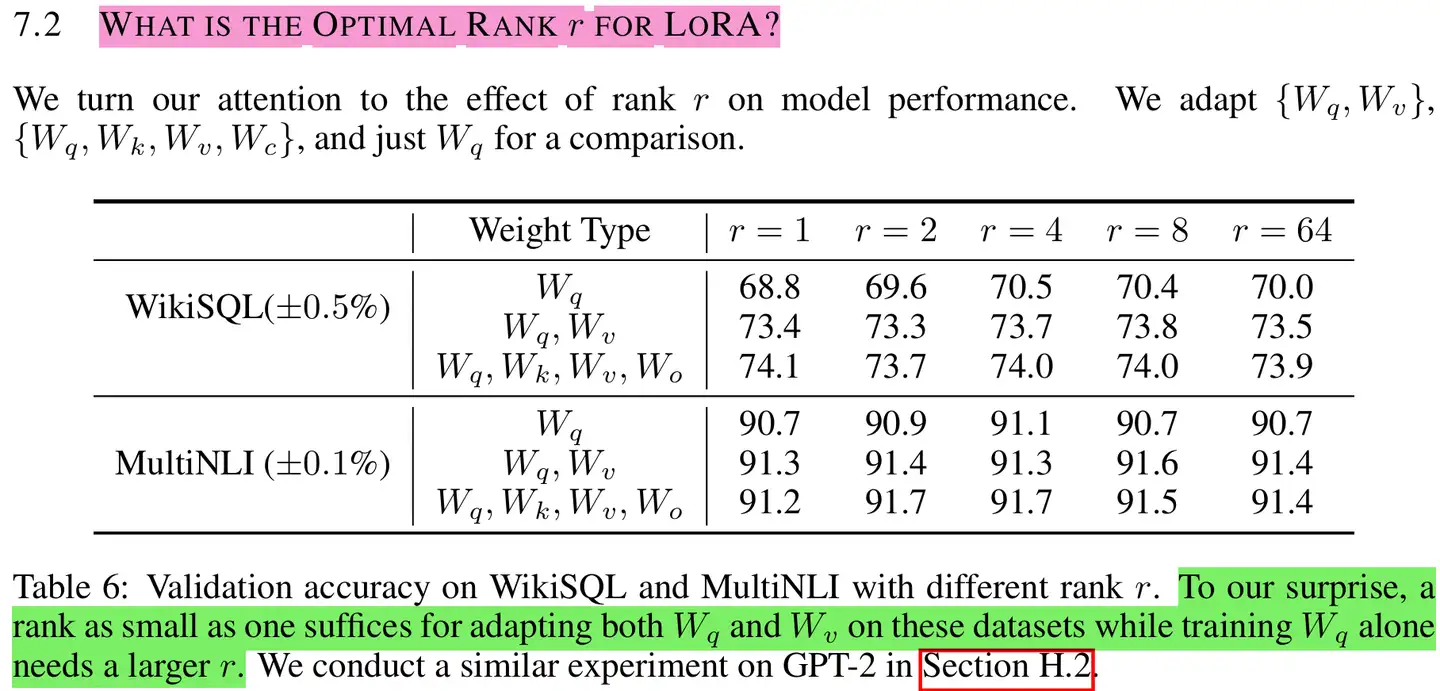
论文基于GPT-3 175B，WikiSQL和MultiNLI数据上，进行了关于LoRA秩\(r\)选取的实验分析

Weight Type指明对Attention的那部分参数做了低秩适应。可以发现，在这个2个数据集上，\(r\)=4,8时基本上要略优于\(r\)=64的效果。更高的\(r\)不一定带来更好的效果。

作者指出，增加\(r\)并不能涵盖更有意义的子空间，这表明低秩适应矩阵就足够了。但是，并不可能期望一个小的\(r\)适用于每个任务或数据集

一些秩\(r\)选取经验：

• 微调的下游任务：
  
  简单任务所需的秩\(r\)不大，任务越难/多任务混合的情况，需要更大的秩\(r\)

• 基座能力：
  
  越强的基座，所需的秩\(r\)应该更小。例如Qwen2-72B-Instruct对比Qwen2-7B-Instruct。

越强的基座在处理同等任务时，需要微调的样本数也通常会更少些。

• 数据规模：
  
  数据规模越大，需要更大的秩\(r\)

1.8 LoRA的微调的参数选取

LoRA原始论文只研究了注意力参数\(\mathbf{W_q}\)、\(\mathbf{W_k}\)、\(\mathbf{W_v}\),和\(\mathbf{W_o}\)。

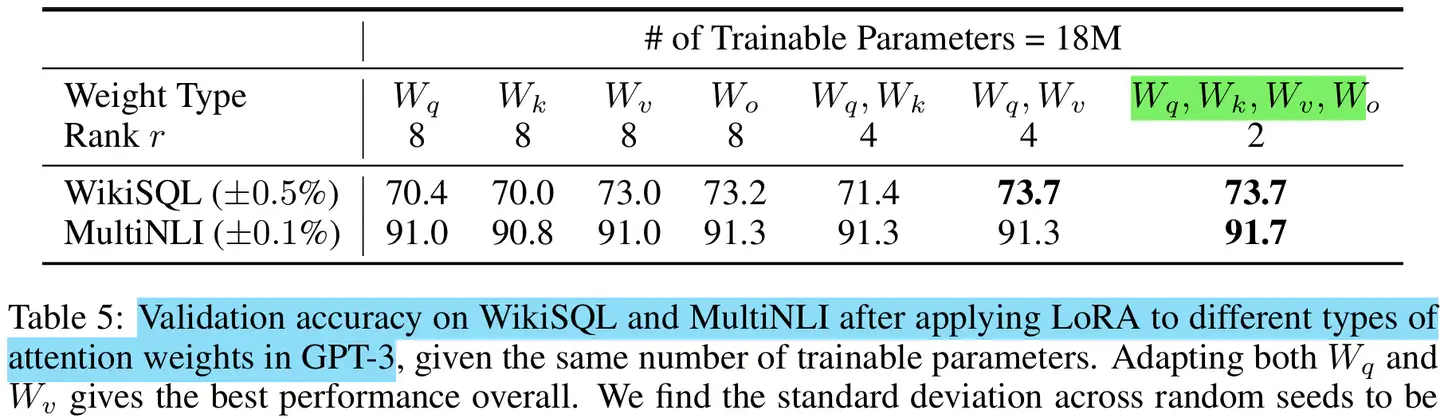
论文基于GPT-3 175B，对比分析了训练预算有限时，关于LoRA的微调注意力参数的选择

在训练预算为18M时 (roughly 35MB if stored

in FP16) on GPT-3 175B，注意力权重全部选择时的效果最佳。

这表明，即使全部的注意力参数即使秩更小时（\(r=2\)），相比秩更大的（\(r=8\)）部分注意力参数，具有更强的建模能力。

在实际中，一般会把FFN的参数也考虑进来。

二、LoRA训练

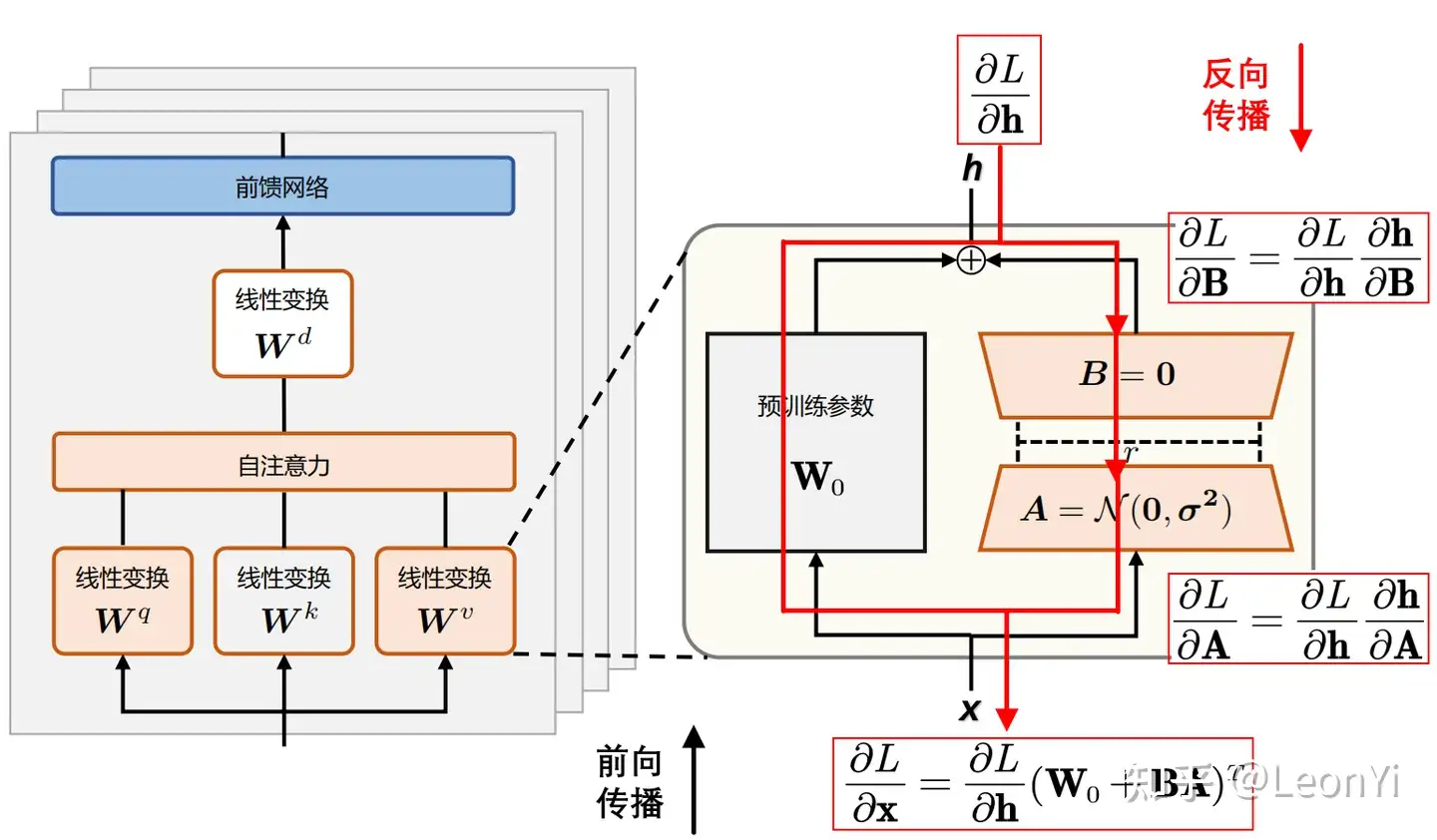
LoRA反向传播的过程

LoRA训练时，将冻结预训练权重 \(\mathbf{W_0}\)

，只优化低秩矩阵 \(\mathbf{B}\)和\(\mathbf{A}\)。

LoRA训练后，只需保存低秩矩阵的\(\mathbf{B}\)和\(\mathbf{A}\)参数。

2.1 LoRA训练的梯度计算

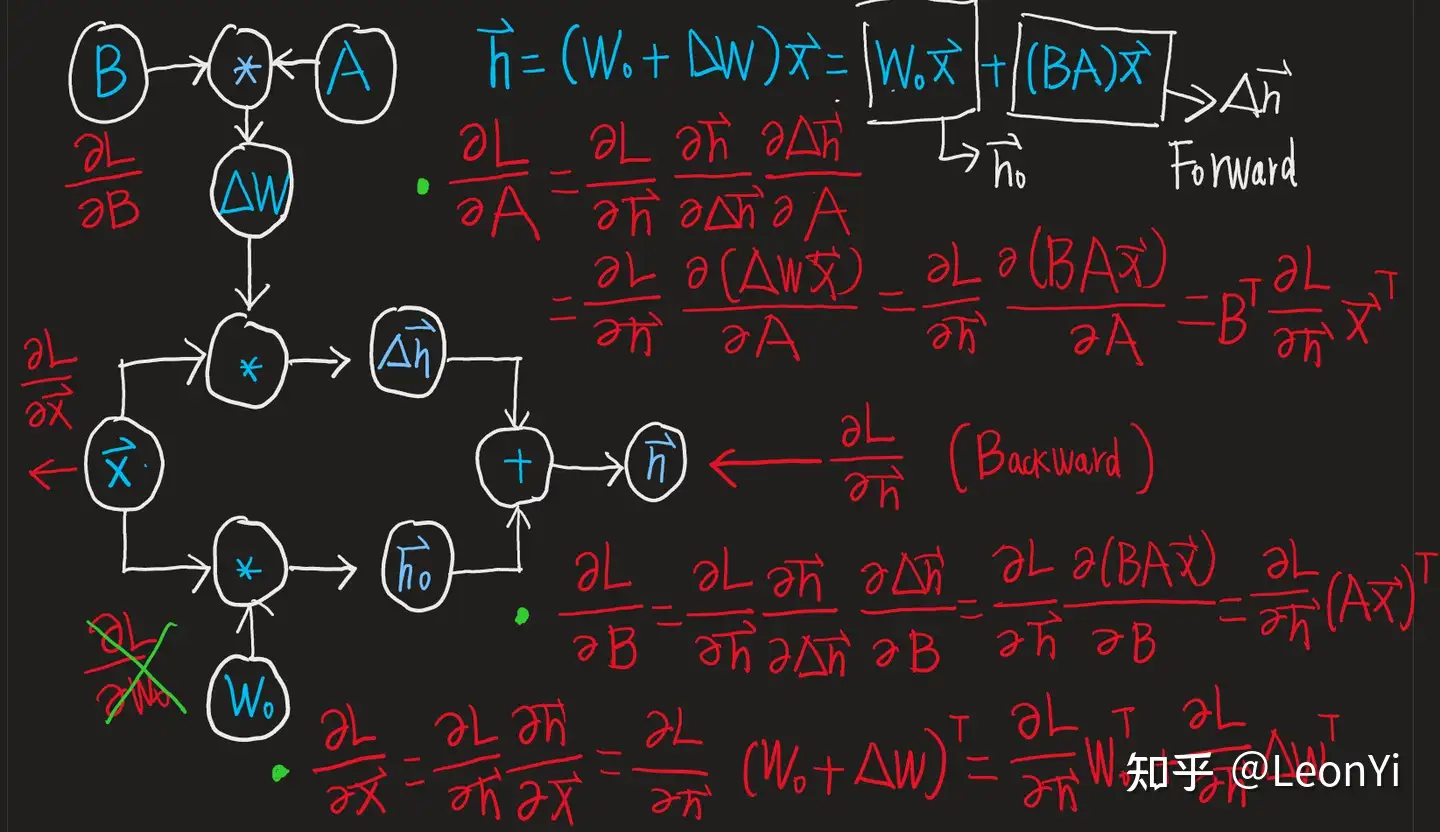
LoRa的计算图和梯度计算

\(\mathbf{B}\) 和 \(\mathbf{A}\)的梯度计算, \(\mathbf{W}_{0}\)不参与计算。

\[\frac{\partial L}{\partial \mathbf{B}} = \frac{\partial L}{\partial \mathbf{h}} \frac{\partial \mathbf{h}}{\partial \Delta \mathbf{h}} \frac{\partial \Delta \mathbf{h}}{\partial \mathbf{B}} = \frac{\partial L}{\partial \mathbf{h}} (\mathbf{Ax})^{\mathsf{T}} \in \mathbb{R}^{d \times r}
\]

\[\frac{\partial L}{\partial \mathbf{A}} = \frac{\partial L}{\partial \mathbf{h}} \frac{\partial \mathbf{h}}{\partial \Delta \mathbf{h}} \frac{\partial \Delta \mathbf{h}}{\partial \mathbf{A}} = \mathbf{B}^{\mathsf{T}} \frac{\partial L}{\partial \mathbf{h}} \mathbf{x}^{\mathsf{T}} \in \mathbb{R}^{r \times d}
\]

继续回传的梯度，包括\(\mathbf{W}_{0}\)这一路：

\[\frac{\partial L}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{h}} \frac{\partial \mathbf{h}}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{h}} (\mathbf{W}_{0} + \mathbf{B}\mathbf{A})^{\mathsf{T}} \in \mathbb{R}^{d}
\]

2.2 反向传播计算量

全量微调前向计算：$ \mathbf{h} = \mathbf{W}_0

\mathbf{x}$

全量微调反向计算：

\[\frac{\partial L}{\partial \mathbf{W}_{0}} = \frac{\partial L}{\partial \mathbf{h}} \frac{\partial \mathbf{h}}{\partial \mathbf{W}_{0}} = \frac{\partial L}{\partial \mathbf{h}} \mathbf{x}^{\mathsf{T}} \in \mathbb{R}^{d \times d}
\]

\[\frac{\partial L}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{h}} \frac{\partial \mathbf{h}}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{h}} \mathbf{W}_{0}^{\mathsf{T}} \in \mathbb{R}^{d }
\]

LoRA微调计算：$\mathbf{h} = \mathbf{W}_{0}\mathbf{x} + \mathbf{B}\mathbf{A} \mathbf{x} $

此时，微调的参数量从原来\(\Delta \mathbf{W}\)的\(d*d\)，变成了\(\mathbf{B}\) 和 \(\mathbf{A}\)的\(2*r*d\)。可知，\(2*r*d << d*d\)（有\(2r << d\)）

不考虑pytorch、llm.c或8-bit优化器、Float8的训练优化实现。可以看到，光梯度计算的话，实际计算量是增加了的。

2.3 LoRA在哪里减少了显存占用

\(\mathbf{B}\)和\(\mathbf{A}\)的梯度是小头这里，暂时忽略。

预训练权重 \(\mathbf{W_0}\)的梯度存储开销，实际就是LoRA能大大减少了显存占用的关键。

在LoRA训练时，\(\mathbf{W_0}\)仍然会参与前向传播和反向传播，但是不会计算其对应梯度\(\frac{\partial L}{\partial \mathbf{W}_0}\)，更不会更新其参数。

因此，这一步不再需要计算和保存梯度\(\frac{\partial L}{\partial \mathbf{W}_0}\)，以及更新\(\mathbf{W_0}\)。

以\(d=4096, r=16\)为例，这部分减少的梯度显存占用粗略估计为：\(d*d - 2*d*r = 1 - \frac{2r}{d}\), 减少了99.2187%。

若以Adaw optimizer的视角来看，其优化器所需维护的states（梯度的一阶矩（均值）和二阶原始矩（有偏方差）），那么显存占用减少地更多。

三、效率分析

按照LoRA论文报告的结果，LoRA微调使得在训练GPT3 175B时的，显存消耗从1.2TB降至350GB；

当\(r=4\)时，最终保存的模型从350GB降至35MB，极大降低了训练的开销。

下表，来源于LlamaFactory Github展示的微调LLM的最小硬件依赖估算值。

方法	精度	7B	13B	30B	70B	8x7B	8x22B
Full	AMP	120GB	240GB	600GB	1200GB	900GB	2400GB
Full	16	60GB	120GB	300GB	600GB	400GB	1200GB
Freeze	16	20GB	40GB	80GB	200GB	160GB	400GB
LoRA/GaLore/BAdam	16	16GB	32GB	64GB	160GB	120GB	320GB
QLoRA	8	10GB	20GB	40GB	80GB	60GB	160GB
QLoRA	4	6GB	12GB	24GB	48GB	30GB	96GB
QLoRA	2	4GB	8GB	16GB	24GB	18GB	48GB

实际的使用情况：

• 一张16GB显存 T4，仅够6B或7B的模型在batchsize为1时，进行int4 QLoRA，这还只是考虑输入输出有限时。
• 一张32GB显存 V100，大致够6B或7B的模型在batchsize为1时，进行LoRA微调。
• 一张80GB显存 A800，Qwen1.5 72B 进行int4 QLoRA，以及例如Baichuan13B / Qwen14B的LoRA微调
• 2张A800 80GB显存，可以进行全参SFT或增量SFT

参考资料

猛猿：图解大模型微调系列之：大模型低秩适配器LoRA（原理篇）

LoRA 微调-MartinLwx's blog|

Parameter-Efficient LLM Finetuning With Low-Rank Adaptation (LoRA)

原创不易，转载需注明出处！