【LeetCode二叉树#05】平衡二叉树

力扣题目链接(opens new window)](https://leetcode.cn/problems/balanced-binary-tree/)

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false

概念：平衡二叉树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

如图：

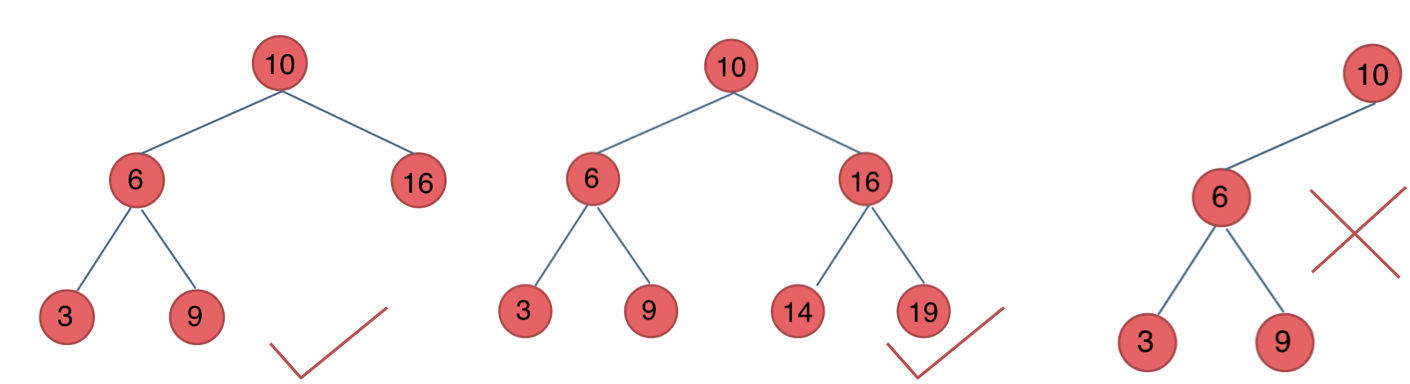
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_set底层实现是哈希表

思路

使用递归回溯的方式解决

既然涉及到了平衡二叉树，那么肯定与去高度计算有关，故需要使用后序遍历来做

因为求深度可以从上到下去查 所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

还是递归三部曲：

1、确定递归函数的参数和返回值

一般来说，我们希望：

参数是二叉树当前节点，返回值为以当前节点为根节点计算的高度

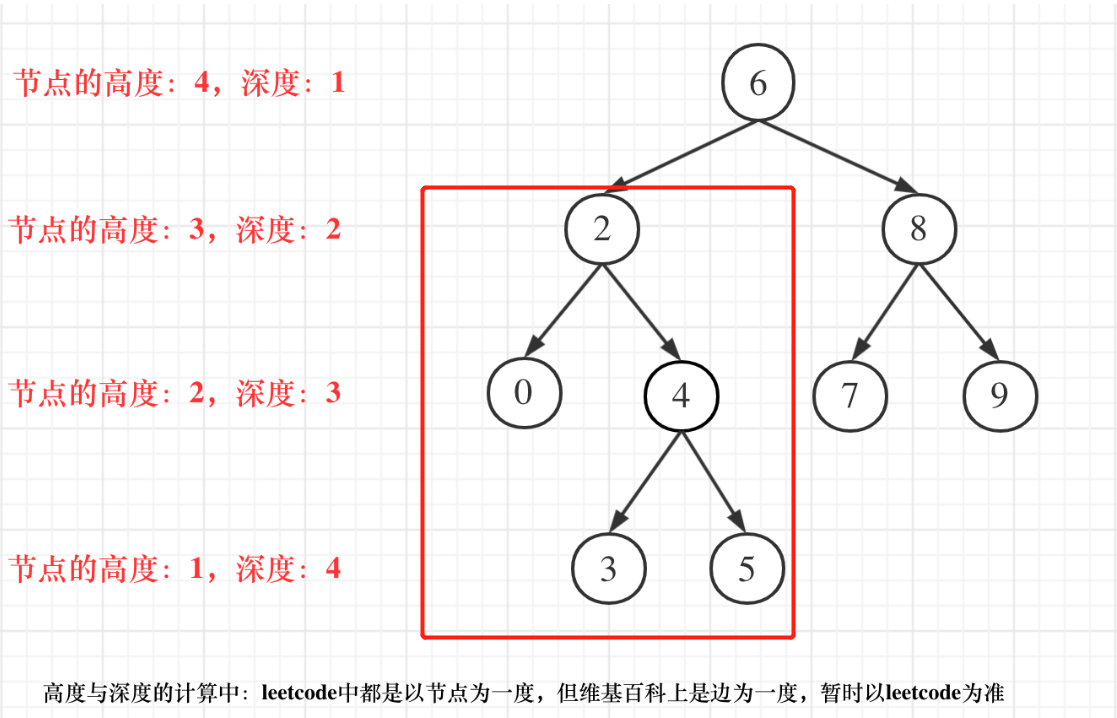
举个例子，假设传入节点是2，那么以2为根节点计算的二叉树的高度（红框中的）为3

但是如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。

所以如果已经不是二叉平衡树了，可以规定返回-1 来标记已经不符合平衡树的规则了

再来更新一下参数和返回值：

参数是二叉树当前节点，返回值是 -1（不满足平衡二叉树时） 或 以当前节点为根节点计算的高度

// -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)

2、确定终止条件

如果传入的当前节点为空，那么当前树没有高度，递归行为也就应该终止

if (node == NULL) {
    return 0;
}

3、明确单层递归逻辑

判断平衡二叉树的依据是当前节点（也就是根节点）的左右子树高度的差值

那么就得分别求出左右子树高度，然后求差值的绝对值，判断是否满足平衡条件

		//明确单层处理逻辑
        //递归计算当前节点的左子节点的高度
        int leftHeight = getHeight(node->left);
        //若发现不平衡，返回-1
        if(leftHeight == -1)return -1;//左

        //递归计算当前节点的左子节点的高度
        int rightHeight = getHeight(node->right);
        if(rightHeight == -1)return -1;//右

        //计算当前节点左右子树的高度差
        int res;
        if(abs(leftHeight - rightHeight) > 1){//差值大于1，不满足条件
            res = -1;
        }else{//满足平衡条件，返回以当前节点为根节点的树的最大高度
            res = 1 + max(leftHeight, rightHeight);
        }
        return res;

代码

class Solution {
public:
    //确定递归函数参数和返回值
    int getHeight(TreeNode* node){
        //确定终止条件
        if(node == NULL) return 0;
        //明确单层处理逻辑
        //递归计算当前节点的左子节点的高度
        int leftHeight = getHeight(node->left);
        //若发现不平衡，返回-1
        if(leftHeight == -1)return -1;//左

        //递归计算当前节点的左子节点的高度
        int rightHeight = getHeight(node->right);
        if(rightHeight == -1)return -1;//右

        //计算当前节点左右子树的高度差
        int res;
        if(abs(leftHeight - rightHeight) > 1){//差值大于1，不满足条件
            res = -1;
        }else{//满足平衡条件，返回以当前节点为根节点的树的最大高度
            res = 1 + max(leftHeight, rightHeight);
        }
        return res;
    }

    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false: true;
    }
};