# [NOIP2011 提高组] 铺地毯

传送锚点：https://www.luogu.com.cn/problem/P1003

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 \(n\) 张地毯，编号从 \(1\) 到 \(n\)。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 \(n + 2\) 行。

第一行，一个整数 \(n\)，表示总共有 \(n\) 张地毯。

接下来的 \(n\) 行中，第 \(i+1\) 行表示编号 \(i\) 的地毯的信息，包含四个整数 \(a ,b ,g ,k\)，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 \((a, b)\) 以及地毯在 \(x\) 轴和 \(y\) 轴方向的长度。

第 \(n + 2\) 行包含两个整数 \(x\) 和 \(y\)，表示所求的地面的点的坐标 \((x, y)\)。

输出格式

输出共 \(1\) 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

样例 #1

样例输入 #1

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

样例输出 #1

3

样例 #2

样例输入 #2

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

样例输出 #2

-1

提示

【样例解释 1】

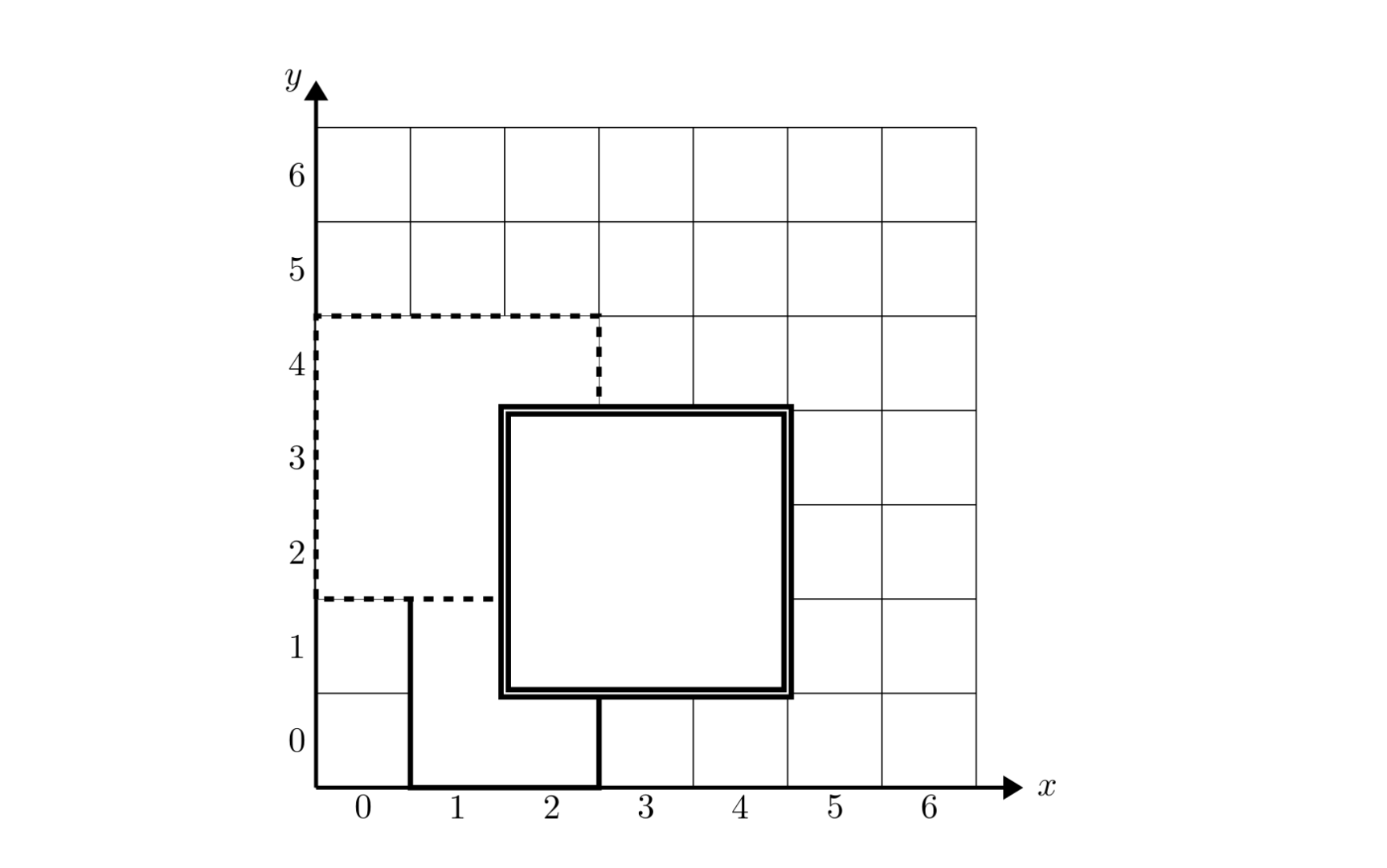
如下图，\(1\) 号地毯用实线表示，\(2\) 号地毯用虚线表示，\(3\) 号用双实线表示，覆盖点 \((2,2)\) 的最上面一张地毯是 \(3\) 号地毯。

【数据范围】

对于 \(30\%\) 的数据，有 \(n \le 2\)。

对于 \(50\%\) 的数据，\(0 \le a, b, g, k \le 100\)。

对于 \(100\%\) 的数据，有 \(0 \le n \le 10^4\), \(0 \le a, b, g, k \le {10}^5\)。

noip2011 提高组 day1 第 \(1\) 题。

思路：

利用结构体存储地毯左下角和右上角在x、y面坐标，然后我们在倒序遍历，如果查找的点在当前所遍历地毯内，直接输出编号，如果遍历完仍没有，则输出-1

code

#include <iostream>
using namespace std;
const int N = 1e4 + 10;
struct Carpet{
    int a,b,c,d;//c、d分别为毛毯右上角横、纵坐标
} carpet[N];
int main() {
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++){
        int a,b,len_x,len_y;
        cin >> a >> b >> len_x >> len_y;
        carpet[i].a = a;
        carpet[i].b = b;
        carpet[i].c = a + len_x;
        carpet[i].d = b + len_y;
    }
    int x,y;
    cin >> x >> y;
    bool flag = false;//看是否被覆盖
    for(int i = n; i >= 1; i--){
        if(x >= carpet[i].a && x <= carpet[i].c){
            if(y >= carpet[i].b && y <= carpet[i].d){
                cout << i << endl;
                return 0;
            }
        }

    }
    if(!flag){
        cout << "-1" << endl;
    }
    return 0;
}