左神算法书籍《程序员代码面试指南》——3_05Morris遍历二叉树的神级方法【★★★★★】

【问题】介绍一种时间复杂度O(N)，额外空间复杂度O(1)的二叉树的遍
历方式，N为二叉树的节点个数
无论是递归还是非递归，避免不了额外空间为O(h)，h 为二叉树的高度
使用morris遍历，即利用空节点空间
morris遍历：
【思路：】
空间复杂度O(1)的要求很严格。常规的递归实现是显然不能满足要求的[其空间复杂度是树的深度O(h)]。本篇文章介绍著名的Morris遍历，该方法利用了二叉树结点中大量指向null的指针。

常规的栈结构遍历方式，遍历到某个节点之后并不能回到上层的结点，这是由二叉树本身的结构所限制的，每个结点并没有指向父节点的指针，因此需要使用栈来完成回到上层结点的步骤。

Morris遍历避免了使用栈结构，让下层有指向上层的指针，但并不是所有的下层结点都有指向上层的指针([这些指针也称为空闲指针])。

要使用O(1)空间进行遍历，最大的难点在于，遍历到子节点的时候怎样重新返回到父节点（假设节点中没有指向父节点的p指针），由于不能用栈作为辅助空间。为了解决这个问题，Morris方法用到了线索二叉树（threaded binary tree）的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱（predecessor）和后继节点（successor），只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。
Morris只提供了中序遍历的方法，在中序遍历的基础上稍加修改可以实现前序，而后续就要再费点心思了。所以先从中序开始介绍。

一、中序遍历步骤：

1. 来到当前节点cur, 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点, 即cur = cur->right。
2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点, 即找到当前节点左子树上的最右节点，记为mostRight
a) 如果mostRight的右孩子为空，将它的右孩子设置指向为当前节点cur。当前节点更新为当前节点的左孩子, 即cur = cur->left。
b) 如果mostRight的右孩子为当前节点cur，将它的右孩子重新设为空（恢复树的形状）。输出当前节点。当前节点更新为当前节点的右孩子， 即cur = cur->right。
3. 重复以上1、2直到当前节点为空。
图示：

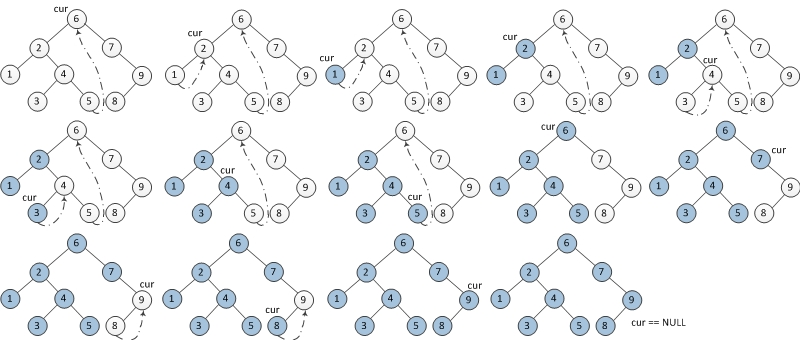
下图为每一步迭代的结果（从左至右，从上到下），cur代表当前节点，深色节点表示该节点已输出。

代码：

         //中序遍历
 void morrisIn(Node* head)
 {
     if(head==null)
         return;
     Node* cur1=head;
     Node* cur2=null;
     while(cur1 ！=  null)
     {
         cur2=cur1.left;
         if(cur2 != null)
         {
             while(cur2.right != null && cur2.right !=cur1)
                 cur2=cur2. right; //找到最右节点
             if(cur2. right==null)
             {
                 cur2. right=cur1; //辅助节点
                 cur1=cur1. left;
                 continue;
             }
             else
                 cur2. right=null;
         }
         cout<<cur1.value<<" ";
         cur1=cur1. right;
     }
     cout<<endl;
 }

复杂度分析：
空间复杂度：O(1)，因为只用了两个辅助指针。
时间复杂度：O(n)。证明时间复杂度为O(n)，最大的疑惑在于寻找中序遍历下二叉树中所有节点的前驱节点的时间复杂度是多少，即以下两行代码：
1 while (prev->right != NULL && prev->right != cur)
2 prev = prev->right;
直觉上，认为它的复杂度是O(nlgn)，因为找单个节点的前驱节点与树的高度有关。但事实上，寻找所有节点的前驱节点只需要O(n)时间。n个节点的二叉树中一共有n - 1条边，整个过程中每条边最多只走2次，一次是为了定位到某个节点，另一次是为了寻找上面某个节点的前驱节点，如下图所示，其中红色是为了定位到某个节点，黑色线是为了找到前驱节点。所以复杂度为O(n)。

二、前序遍历

前序遍历与中序遍历相似，代码上只有一行不同，不同就在于输出的顺序。
步骤：
1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。
2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
a) 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。输出当前节点（在这里输出，这是与中序遍历唯一一点不同）。当前节点更新为当前节点的左孩子。
b) 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。当前节点更新为当前节点的右孩子。
3. 重复以上1、2直到当前节点为空。
图示：

代码：

         //前序遍历
 void morrisIn(Node* head)
 {
     if(head==null)
         return;
     Node* cur1=head;
     Node* cur2=null;
     while(cur1 ！=  null)
     {
         cur2=cur1.left;
         if(cur2 != null)
         {
             while(cur2.right != null && cur2.right !=cur1)
                 cur2=cur2. right; //找到最右节点
             if(cur2. right==null)
             {
                 cur2. right=cur1; //辅助节点
                 cout << cur1.value << " ";//前序遍历是先打印
                 cur1=cur1. left;
                 continue;
             }
             else
                 cur2. right=null;
         }
         else
             cout<<cur1.value<<" ";
         cur1=cur1. right;
     }
     cout << endl;
 }

复杂度分析：
时间复杂度与空间复杂度都与中序遍历时的情况相同。

三、后序遍历
后续遍历稍显复杂，需要建立一个临时节点dump，令其左孩子是root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。
步骤：
当前节点设置为临时节点dump。
1. 如果当前节点的左孩子为空，则将其右孩子作为当前节点。
2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
a) 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。
b) 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右孩子。
3. 重复以上1、2直到当前节点为空。
图示：

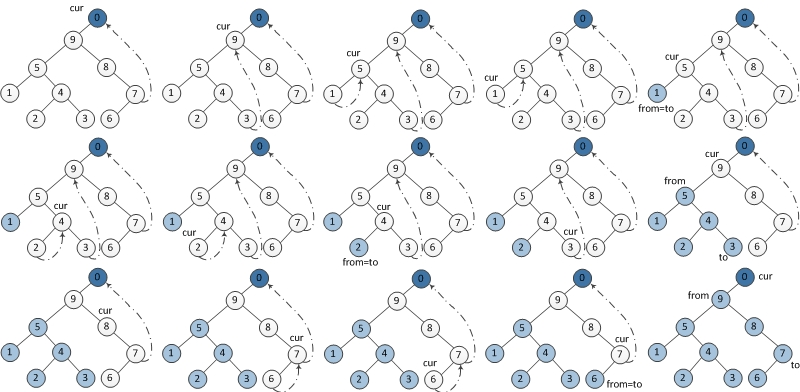
代码：

         //后序遍历
 Node* reverseEdge(Node* from)
 {
     Node* pre=null;
     Node* next=null;
     while(from != null)
     {
         next=from. right;
         from.right=pre;
         pre=from;
         from=next;
     }
     return pre;
 }
         void printEdge(Node* head)
 {
     Node* tail=reverseEdge(head);
     Node* cur=tail;
     while(cur!=null)
     {
         cout << cur.value << " ";
         cur=cur. right;
     }
     reverseEdge(tail);
 }
 void morrisPos(Node* head)
 {
     if(head==null)
         return;
     Node* cur1=head;
     Node* cur2=null;
     while(cur1 ！= null)
     {
         cur2=cur1.left;
         if(cur2！=null)
         {
             while(cur2.right ！= null && cur2.right！= cur1)
                 cur2=cur2.right;//找到最右节点
             if(cur2.right==null)
             {
                 cur2.right=cur1;
                 cur1=cur1.left;
                 continue;
             }
             else
             {
                 cur2.right=null;
                 printEdge(cur1.left);
             }
         }
         cur1=cur1. right;
     }
     printEdge(head);
     cout << endl;
 }

复杂度分析：

空间复杂度同样是O(1)；时间复杂度也是O(n)，倒序输出过程只不过是加大了常数系数。