今天讲了DFA，最小生成树以及最短路

　　DFA（接着昨天讲）

　　如何高效的构造前缀指针：

　　步骤为：根据深度一一求出每一个节点的前缀指针。对于当前节点，设他的父节点与他的边上的字符为Ch，如果他的父节点的前缀指针所指向的节点的儿子中，有通过Ch字符指向的儿子，那么当前节点的前缀指针指向该儿子节点，否则通过当前节点的父节点的前缀指针所指向点的前缀指针，继续向上查找，直到到达根节点为止。

　　ps：构造前缀指针时在最前面加一个0号节点。

　　对于一个插入了n个模式串的单词 前缀树构造其前缀指针的时间复杂 度为：O(∑len(i)) (i=1..n)

　　如何在建立好的Trie图上遍历：

　　遍历的方法如下：从ROOT出发，按照当前串的下一 个字符ch来进行在树上的移动。若当前点P不存在通过ch连接的儿子，那么考虑P的前缀指针指向的节点Q，如果还无法找到通过ch连接的儿子节点，再考虑Q的前缀指针… 直到找到通过ch连接的儿子，再继续遍历。如果遍历过程中经过了某个终止节点，则说明S包含该终止节点代表的模式串. 如果遍历过程中经过了某个非终止节点的危险节点， 则可以断定S包含某个模式串。要找出是哪个，沿着危险节点的前缀指针链走，碰到终止节点即可。

　　ps:   危险节点：1） 终止节点是危险节点        2) 如果一个节点的前缀指针指向危险节点，那么它也是危险节点。

　　　　这样遍历一个串S的时间复杂度是O(len(S))

　　最纯粹的Trie图题目：

  1. 给N个模式串，每个不超过个字符，再给M个句子，句子长度<
  2.  判断每个句子里是否包含模式串
  3. N < , M <  ,字符都是小写字母
  4.  
  5. abcde
  6. defg
  7. cdke
  8. ab
  9. f
  10. abcdkef
  11. abkef
  12. bcd
  13. bca
  14. add
  15. ab
  16. qab
  17. f

题目

  1.  #include <iostream>
  2.  #include <cstdio>
  3.  #include <cstring>
  4.  #include <vector>
  5.  #include <queue>
  6.  using namespace std;
  7.  #define LETTERS 26
  8.  int nNodesCount = ;
  9.  struct CNode
  10.  {
  11.      CNode * pChilds[LETTERS];
  12.      CNode * pPrev; //前缀指针
  13.      bool bBadNode; //是否是危险节点
  14.      void Init()
  15.      {
  16.          memset(pChilds,,sizeof(pChilds));
  17.          bBadNode = false;
  18.          pPrev = NULL;
  19.      }
  20.  };
  21.  CNode Tree[]; //10个模式串，每个10个字符，每个字符一个节点，也只要100个节点
  22.  
  23.  void Insert( CNode * pRoot, char * s)
  24.  {
  25.      //将模式串s插入trie树
  26.      for( int i = ; s[i]; i ++ )
  27.      {
  28.          if( pRoot->pChilds[s[i]-'a'] == NULL)
  29.          {
  30.              pRoot->pChilds[s[i]-'a'] =Tree + nNodesCount;
  31.              nNodesCount ++;
  32.          }
  33.          pRoot = pRoot->pChilds[s[i]-'a'];
  34.      }
  35.      pRoot-> bBadNode = true;
  36.  }
  37.  void BuildDfa( )
  38.  {
  39.      //在trie树上加前缀指针
  40.      for( int i = ; i < LETTERS ; i ++ )
  41.          Tree[].pChilds[i] = Tree + ;
  42.      Tree[].pPrev = NULL;
  43.      Tree[].pPrev = Tree;
  44.      deque<CNode * > q;
  45.      q.push_back(Tree+);
  46.      while( ! q.empty() )
  47.      {
  48.          CNode * pRoot = q.front();
  49.          q.pop_front();
  50.          for( int i = ; i < LETTERS ; i ++ )
  51.          {
  52.              CNode * p = pRoot->pChilds[i];
  53.              if( p)
  54.              {
  55.                  CNode * pPrev = pRoot->pPrev;
  56.                  while( pPrev )
  57.                  {
  58.                      if( pPrev->pChilds[i] )
  59.                      {
  60.                          p->pPrev = pPrev->pChilds[i];
  61.                          if( p->pPrev-> bBadNode)
  62.                              p-> bBadNode = true;
  63.  //自己的pPrev指向的节点是危险节点，则自己也是危险节点
  64.                          break;
  65.                      }
  66.                      else
  67.                          pPrev = pPrev->pPrev;
  68.                  }
  69.                  q.push_back(p);
  70.              }
  71.          }
  72.      } //对应于while( ! q.empty() )
  73.  }
  74.  bool SearchDfa(char * s)
  75.  {
  76.      //返回值为true则说明包含模式串
  77.      CNode * p = Tree + ;
  78.      for( int i = ; s[i] ; i ++ )
  79.      {
  80.          while(true)
  81.          {
  82.              if( p->pChilds[s[i]-'a'])
  83.              {
  84.                  p = p->pChilds[s[i]-'a'];
  85.                  if( p-> bBadNode)
  86.                      return true;
  87.                  break;
  88.              }
  89.              else
  90.                  p = p->pPrev;
  91.          }
  92.      }
  93.      return false;
  94.  }
  95.  int main()
  96.  {
  97.      nNodesCount = ;
  98.      int M,N;
  99.      scanf("%d%d",&N,&M); //N个模式串，M个句子
  100.      for( int i = ; i < N; i ++ )
  101.      {
  102.          char s[];
  103.          scanf("%s",s);
  104.          Insert(Tree + ,s);
  105.      }
  106.      BuildDfa();
  107.      for( int i =  ; i < M; i ++ )
  108.      {
  109.          char s[];
  110.          scanf("%s",s);
  111.          cout << SearchDfa(s) << endl;
  112.      }
  113.      return ;
  114.  }

代码

PS：有可能模式串A是另一模式串B的子串，此情况下可能只能得出匹配B的结论而忽略也匹配A，所以不能只看终止节点，还要看危险节点：

　　　对每个节点设置一个“是否计算过”的标记，当标记一个危险节点为“已匹配”时，沿该节点对应的S的所有后缀指针一直到根节点全标记为“已匹配”。

例题：1.POJ3987 Computer Virus on Planet Pandora 2010 福州赛区题目

　　　2.POI #7 题：病毒

　　　3.POJ 3691 DNA repair

　　　4.POJ 1625 Censored!

　　　5.POJ2778 DNA Sequence

　　最小生成树(MST)问题

　　 生成树：

　　1.无向连通图的边的集合

　　2.无回路

　　3.连接所有的点

　　最小：         所有边的权值之和最小

　　有n个顶点，n-1条边

　　Prim算法

　　假设G=(V,E)是一个具有n个顶点的连通网， T=(U,TE)是G的最小生成树，U,TE初值均为空集。

　　首先从V中任取一个顶点（假定取v1），将它并入U中，此时U={v1}，然后只要U是V的真子集(U∈V)， 就从那些一个端点已在T中，另一个端点仍在T外 的所有边中，找一条最短边，设为(vi ,vj ),其中 vi∈U,vj∈V-U，并把该边(vi , vj )和顶点vj分别并入T 的边集TE和顶点集U，如此进行下去，每次往生成树里并入一个顶点和一条边，直到n-1次后得到最小生成树。

　　关键问题：每次如何从连接T中和T外顶点的所有边中，找 到一条最短的

　　　　1) 如果用邻接矩阵存放图，而且选取最短边的时候遍历所有点进行选取，则总时间复杂度为 O(V2 ), V为顶点个数

　　　　2)用邻接表存放图,并使用堆来选取最短边，则总时间复杂度为O(ElogV)

　　　　不加堆优化的Prim 算法适用于密集图，加堆优化的适用于稀疏图

　　Kruskal算法

　　假设G=(V,E)是一个具有n个顶点的连通网， T=(U,TE)是G的最小生成树，U=V,TE初值为 空。

　　将图G中的边按权值从小到大依次选取，若选取的边使生成树不形成回路，则把它并入TE中，若形成回路则将其舍弃，直到TE 中包含N-1条边为止，此时T为最小生成树。

　　关键问题：如何判断欲加入的一条边是否与生成树 中边构成回路。

　　　　利用并查集！

　　Kruskal 和 Prim 比较

　　Kruskal:将所有边从小到大加入，在此过程中 判断是否构成回路

　　　　– 使用数据结构：并查集

　　　　– 时间复杂度：O(ElogE)

　　　　 – 适用于稀疏图

　　Prim:从任一节点出发，不断扩展

　　　　– 使用数据结构：堆

　　　　– 时间复杂度：O(ElogV) 或 O(VlogV+E)(斐波那契堆）

　　　　– 适用于密集图

　　　　– 若不用堆则时间复杂度为O(V2)

例题：1.POJ 1258 Agri-Net

　　　2.POJ 2349 Arctic Network

　　　3. 2011 ACM/ICPC亚洲区预选赛北京赛站

　　　　Problem A. Qin Shi Huang’s National Road System

　　最短路算法

　　Dijkstra 算法   解决无负权边的带权有向图 或 无向图的单源最短路问题

　　用邻接表，不优化，时间复杂度O(V2+E)

　　Dijkstra+堆的时间复杂度 o(ElgV)

　　用斐波那契堆可以做到O(VlogV+E)

　　若要输出路径，则设置prev数组记录每个节点的前趋点，在d[i] 更新时更新prev[i]

　　Dijkstra算法实现：

　　　　已经求出到V0点的最短路的点的集合为T

　　　　维护Dist数组，Dist[i]表示目前Vi到V0的“距离”

　　　　开始Dist[0] = 0, 其他Dist[i] = 无穷大, T为空集

　　　1) 若|T| = N，算法完成，Dist数组就是解。否则取Dist[i]最 小的不在T中的点Vi, 将其加入T，Dist[i]就是Vi到V0的最短 路长度。

　　　2) 更新所有与Vi有边相连且不在T中的点Vj的Dist值：  Dist[j] = min(Dist[j],Dist[i]+W(Vi,Vj))

　　　3) 转到1）

例题：1.POJ 3159 Candies

　　Bellman-Ford算法

　　解决含负权边的带权有向图的单源最短路径问题

　　不能处理带负权边的无向图(因可以来回走一条负权边)

　　限制条件： 要求图中不能包含权值总和为负值回路(负权值回路)，如下图所示。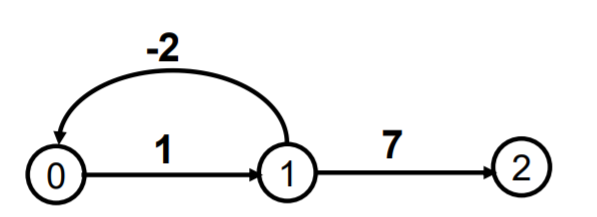 

　　Bellman-Ford算法思想：

　　　　构造一个最短路径长度数组序列dist 1 [u], dist 2 [u], …, dist n-1 [u] （u = 0,1…n-1,n为点数)

　　　　dist n-1 [u]为从源点v出发最多经过不构成负权值回路的n-1条边到达终点u的 最短路径长度；

　　　　算法的最终目的是计算出dist n-1 [u]，为源点v到顶点u的最短路径长度。

　　　　递推公式(求顶点u到源点v的最短路径)：

　　　　　　dist 1 [u] = Edge[v][u]

　　　　　　dist k [u] = min{ dist k-1 [u], min{ dist k-1 [j] + Edge[j][u] } }, j=0,1,…,n-1,j≠u

　　若存在dist n [u]  < dist n-1 [u]，则说明存在从源点可达的负权值回路

　　　在求出distn-1[ ]之后，再对每条边<u,k>判断一下：加入这条边是否会使得顶点k的最短路径值再缩短，即判断：dist[u]+w(u,k)<dist[k]否成立，如果成立，则说明存在从源点可达的负权值回路。

　　存在负权回路就一定能导致该式成立的证明:

　　如果成立，则说明找到了一条经过了n条边的从 s 到k的路径，且 其比任何少于n条边的从s到k的路径都短。

　　一共n个顶点，路径却经过了n条边，则必有一个顶点m经过了至少 两次。则m是一个回路的起点和终点。走这个回路比不走这个回路 路径更短，只能说明这个回路是负权回路。

　　

　　Bellman-Ford算法改进:

　　Bellman-Ford算法不一定要循环n-1次，n为顶点个数,只要在某次循环过程中，考虑每条边后，源点到所有顶点的最短路径 长度都没有变，那么Bellman-Ford算法就可以提前结束了

　　Dijkstra算法与Bellman-Ford算法的区别

　　Dijkstra算法和Bellman算法思想有很大的区别：

　　　　Dijkstra算法在求解过程中，源点到集合S内各顶点的最短路径一旦求出，则之后不变了，修改的仅仅是源点到S外各顶点的最短路径长度。

　　　　Bellman-Ford算法在求解过程中，每次循环都要修改所有顶点的dist[ ]，也就是说源点到各顶点最短路径长度一 直要到算法结束才确定下来。

例题：1.POJ 3259 Wormholes

  1. 要求判断任意两点都能仅通过正边就互相可达的有向图(图中有
  2. 重边）中是否存在负权环
  3. Sample Input
  4.  
  5. Sample Output
  6. NO
  7. YES
  8.  
  9. 2个test case
  10. 每个test case 第一行：
  11. N M W (N<=,M<=,W<=)
  12. N个点
  13. M条双向正权边
  14. W条单向负权边
  15. 第一个test case 最后一行
  16.  
  17. 是单向负权边，->1的边权值是-

题目

  1.  //by guo wei
  2.  #include <iostream>
  3.  #include <vector>
  4.  using namespace std;
  5.  int F,N,M,W;
  6.  const int INF =  << ;
  7.  struct Edge
  8.  {
  9.      int s,e,w;
  10.      Edge(int ss,int ee,int ww):s(ss),e(ee),w(ww) { }
  11.      Edge() { }
  12.  };
  13.  vector<Edge> edges; //所有的边
  14.  int dist[];
  15.  int Bellman_ford(int v)
  16.  {
  17.      for( int i = ; i <= N; ++i)
  18.          dist[i] = INF;
  19.      dist[v] = ;
  20.      for( int k = ; k < N; ++k)   //经过不超过k条边
  21.      {
  22.          for( int i = ; i < edges.size(); ++i)
  23.          {
  24.              int s = edges[i].s;
  25.              int e = edges[i].e;
  26.              if( dist[s] + edges[i].w < dist[e])
  27.                  dist[e] = dist[s] + edges[i].w;
  28.          }
  29.      }
  30.      for( int i = ; i < edges.size(); ++ i)
  31.      {
  32.          int s = edges[i].s;
  33.          int e = edges[i].e;
  34.          if( dist[s] + edges[i].w < dist[e])
  35.              return true;
  36.      }
  37.      return false;
  38.  }
  39.  int main()
  40.  {
  41.      cin >> F;
  42.      while( F--)
  43.      {
  44.          edges.clear();
  45.          cin >> N >> M >> W;
  46.          for( int i = ; i < M; ++ i)
  47.          {
  48.              int s,e,t;
  49.              cin >> s >> e >> t;
  50.              edges.push_back(Edge(s,e,t)); //双向边等于两条边
  51.              edges.push_back(Edge(e,s,t));
  52.          }
  53.          for( int i = ; i < W; ++i)
  54.          {
  55.              int s,e,t;
  56.              cin >> s >> e >> t;
  57.              edges.push_back(Edge(s,e,-t));
  58.          }
  59.          if( Bellman_ford())//从1可达所有点
  60.              cout << "YES" <<endl;
  61.          else cout << "NO" <<endl;
  62.      }
  63.  }
  1. for( int k = ; k < N; ++k) { //经过不超过k条边
  2.     for( int i = ;i < edges.size(); ++i) {
  3.         int s = edges[i].s;
  4.         int e = edges[i].e;
  5.         if( dist[s] + edges[i].w < dist[e])
  6.             dist[e] = dist[s] + edges[i].w;
  7. }
  8. }
  9.      会导致在一次内层循环中，更新了某个 dist[x]后，以后又用dist[x]去更新dist[y],这样dist[y]就是经过最多不超过k+1条边的情况了
  10.     出现这种情况没有关系，因为整个 for( int k = ; k < N; ++k) 循环的目的是要确保,对任意点u,如果从源s到u的最短路是经过不超过n-1条边的,则这条最短路不会被忽略。至于计算过程中对某些点 v 计算出了从s->v的经过超过N-1条边的最短路的情况，也不影响结果正确性。若是从s->v的经过超过N-1条边的结果比经过最多N-1条边的结果更小，那一定就有负权回路。有负权回路的情况下，再多做任意多次循环，每次都会发现到有些点的最短路变得更短了。

问题

　　　2.POJ 1860

　　　3.POJ 3259

　　　4.POJ 2240

　　SPFA算法

　　快速求解含负权边的带权有向图的单源最短路径问题

　　是Bellman-Ford算法的改进版，利用队列动态更新dist[]

　　维护一个队列，里面存放所有需要进行迭代的点。初始时队列中只有一个 源点S。用一个布尔数组记录每个点是否处在队列中。

　　每次迭代，取出队头的点v，依次枚举从v出发的边v->u，若 Dist[v]+len(v->u) 小于Dist[u]，则改进Dist[u]（可同时将u前驱记为v）。 此时由于S到u的最短距离变小了，有可能u可以改进其它的点，所以若u不在队列中，就将它放入队尾。这样一直迭代下去直到队列变空，也就是S到所有节点的最短距离都确定下来，结束算法。若一个点最短路被改进的次数达到n ，则有负权环(原因同B-F算法。可以用spfa算法判断图有无负权环

　　在平均情况下，SPFA算法的期望时间复杂度为O(E)。

例题：1.POJ 3259 Wormholes

  1. 要求判断任意两点都能仅通过正边就互相可达的有向图(图中有
  2. 重边）中是否存在负权环
  3. Sample Input
  4.  
  5. Sample Output
  6. NO
  7. YES
  8.  
  9. 2个test case
  10. 每个test case 第一行：
  11. N M W (N<=,M<=,W<=)
  12. N个点
  13. M条双向正权边
  14. W条单向负权边
  15. 第一个test case 最后一行
  16.  
  17. 是单向负权边，->1的边权值是-

题目

  1.  ///POJ3259 Wormholes 判断有没有负权环spfa
  2.  //by guo wei
  3.  #include <iostream>
  4.  #include <vector>
  5.  #include <queue>
  6.  #include <cstring>
  7.  using namespace std;
  8.  int F,N,M,W;
  9.  const int INF =  << ;
  10.  struct Edge
  11.  {
  12.      int e,w;
  13.      Edge(int ee,int ww):e(ee),w(ww) { }
  14.      Edge() { }
  15.  };
  16.  vector<Edge> G[]; //整个有向图
  17.  int updateTimes[]; //最短路的改进次数
  18.  int dist[]; //dist[i]是源到i的目前最短路长度
  19.  int Spfa(int v)
  20.  {
  21.      for( int i = ; i <= N; ++i)
  22.          dist[i] = INF;
  23.      dist[v] = ;
  24.      queue<int> que;
  25.      que.push(v);
  26.      memset(updateTimes,,sizeof(updateTimes));
  27.      while( !que.empty())
  28.      {
  29.          int s = que.front();
  30.          que.pop();
  31.          for( int i = ; i < G[s].size(); ++i)
  32.          {
  33.              int e = G[s][i].e;
  34.              if( dist[e] > dist[s] + G[s][i].w )
  35.              {
  36.                  dist[e] = dist[s] + G[s][i].w;
  37.                  que.push(e); //没判队列里是否已经有e,可能会慢一些
  38.                  ++updateTimes[e];
  39.                  if( updateTimes[e] >= N) return true;
  40.              }
  41.          }
  42.      }
  43.      return false;
  44.  }
  45.  int main()
  46.  {
  47.      cin >> F;
  48.      while( F--)
  49.      {
  50.          cin >> N >> M >> W;
  51.          for( int i = ; i <; ++i)
  52.              G[i].clear();
  53.          int s,e,t;
  54.          for( int i = ; i < M; ++ i)
  55.          {
  56.              cin >> s >> e >> t;
  57.              G[s].push_back(Edge(e,t));
  58.              G[e].push_back(Edge(s,t));
  59.          }
  60.          for( int i = ; i < W; ++i)
  61.          {
  62.              cin >> s >> e >> t;
  63.              G[s].push_back(Edge(e,-t));
  64.          }
  65.          if( Spfa())
  66.              cout << "YES" <<endl;
  67.          else cout << "NO" <<endl;
  68.      }
  69.  }

POJ 3259

　　　 2.POJ 2387

　　　 3.POJ 3256

　　弗洛伊德算法

　　用于求每一对顶点之间的最短路径。有向图，无向图均可，也可以有负权边。但不适合于有负权回路的题。

　　复杂度O(n3)

  1. ///弗洛伊德算法伪代码（三层循环）
  2. for( int i =  ; i <= vtxnum; ++i )
  3.     for( int j = ; j <= vtxnum; ++j)
  4.     {
  5.         dist[i][j] = cost[i][j]; // cost是边权值, dist是两点间最短距离
  6.         if( dist[i][j] < INFINITE) //i到j有边
  7.             path[i,j] = [i]+[j]; //path是路径
  8.     }
  9. for( k = ; k <= vtxnum; ++k) //每次求中间点标号不超过k的i到j最短路
  10.     for( int i = ; i <= vtxnum; ++i)
  11.         for(int j = ; j <= vtxnum ; ++j)
  12.             if( dist[i][k] + dist[k][j] < dist[i][j])
  13.             {
  14.                 dist[i][j] = dist[i][k]+dist[k][j];
  15.                 path[i,j] = path[i,k]+path[k,j];
  16.             }

例题：1.POJ 3660 Cow Contest

　　　2.POJ 1125

ACM北大暑期课培训第六天的更多相关文章

  1. ACM北大暑期课培训第一天

    今天是ACM北大暑期课开课的第一天,很幸运能参加这次暑期课,接下来的几天我将会每天写博客来总结我每天所学的内容.好吧下面开始进入正题: 今天第一节课,郭炜老师给我们讲了二分分治贪心和动态规划. 1.二 ...

  2. ACM北大暑期课培训第七天

    昨天没时间写,今天补下. 昨天学的强连通分支,桥和割点,基本的网络流算法以及Dinic算法: 强连通分支 定义:在有向图G中,如果任意两个不同的顶点 相互可达,则称该有向图是强连通的. 有向图G的极大 ...

  3. ACM北大暑期课培训第二天

    今天继续讲的动态规划 ... 补充几个要点: 1. 善于利用滚动数组(可减少内存,用法与计算方向有关) 2.升维 3.可利用一些数据结构等方法使代码更优  (比如优先队列) 4.一般看到数值小的 (十 ...

  4. ACM北大暑期课培训第八天

    今天学了有流量下界的网络最大流,最小费用最大流,计算几何. 有流量下界的网络最大流 如果流网络中每条边e对应两个数字B(e)和C(e), 分别表示该边上的流量至少要是B(e),最多 C(e),那么,在 ...

  5. ACM北大暑期课培训第五天

    今天讲的扫描线,树状数组,并查集还有前缀树. 扫描线   扫描线的思路:使用一条垂直于X轴的直线,从左到右来扫描这个图形,明显,只有在碰到矩形的左边界或者右边界的时候,这个线段所扫描到的情况才会改变, ...

  6. ACM北大暑期课培训第四天

    今天讲了几个高级搜索算法:A* ,迭代加深,Alpha-Beta剪枝   以及线段树 A*算法 启发式搜索算法(A算法) : 在BFS算法中,若对每个状态n都设定估价函数 f(n)=g(n)+h(n) ...

  7. ACM北大暑期课培训第三天

    今天讲的内容是深搜和广搜 深搜(DFS) 从起点出发,走过的点要做标记,发现有没走过的点,就随意挑一个往前走,走不 了就回退,此种路径搜索策略就称为“深度优先搜索”,简称“深搜”. bool Dfs( ...

  8. 2019暑期北航培训—预培训作业-IDE的安装与初步使用(Visual Studio版)

    这个作业属于那个课程 2019北航软件工程暑期师资培训 这个作业要求在哪里 预培训-IDE的安装与初步使用(Visual Studio版) 我在这个课程的目标是 提高自身实际项目实践能力,掌握帮助学生 ...

  9. 01派【北京大学ACM/ICPC竞赛训练暑期课】

    01:派 总时间限制:  1000ms 内存限制:  65536kB 描述 我的生日要到了!根据习俗,我需要将一些派分给大家.我有N个不同口味.不同大小的派.有F个朋友会来参加我的派对,每个人会拿到一 ...

随机推荐

  1. mac常用快捷键,Mac文件重命名快捷键,Mac OS快速访问系统根目录， MacOS 10.11重要数据的存储位置大全

    command+r,相当于F5,刷新页面 command+F5,启动voiceover command+q 关闭当前程序 在Finder中command+/ 打开底部状态栏,可以查看剩余磁盘空间大小 ...

  2. H3C 配置Basic NAT

  3. [转]vue router基本使用

    第一步:安装 cnpm install vue-router --save 路由配置基本语法 router下index.js引入 import Vue from "vue"; im ...

  4. spring boot + thymeleaf 乱码问题

    spring boot + thymeleaf 乱码问题 hellotrms 发布于 2017/01/17 15:27 阅读 1K+ 收藏 0 答案 1 开发四年只会写业务代码,分布式高并发都不会还做 ...

  5. 【u238】暴力摩托

    Time Limit: 1 second Memory Limit: 64 MB [问题描述] 晚会上大家在玩一款"暴力摩托"的游戏,它拥有非常逼真的画面和音响效果! 当然了,车子 ...

  6. Spring Boot Admin-应用健康监控后台管理

    Spring Boot Admin 用于监控基于 Spring Boot 的应用,它是在 Spring Boot Actuator 的基础上提供简洁的可视化 WEB UI. 1. 什么是Spring ...

  7. TOJ 6121: 学长的情书 ( 二分）

    传送门: 点我 6121: 学长的情书  时间限制(普通/Java):2000MS/6000MS     内存限制:65536KByte总提交: 79            测试通过:2 描述 抹布收 ...

  8. Spring Boot 2.x使用Mockito进行测试

    在上一篇,项目基本实现了Spring Boot对Mybatis的整合.这篇文章使用Mockito对项目进行测试. 1.使用postmat测试: 2.编写单元测试类,使用mockito进行测试: 3.使 ...

  9. POJ - 3415 Common Substrings (后缀数组）

    A substring of a string T is defined as: T( i, k)= TiTi +1... Ti+k -1, 1≤ i≤ i+k-1≤| T|. Given two s ...

  10. jquery简单实现复选框的全选与反选

    <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title> ...