第二十七篇 玩转数据结构——集合（Set）与映射（Map）
1.. 集合的应用
- 集合可以用来去重
- 集合可以用于进行客户的统计
- 集合可以用于文本词汇量的统计
2.. 集合的实现
- 定义集合的接口
Set<E>
·void add(E) // 不能添加重复元素
·void remove(E)
·boolean contains(E)
·int getSize()
·boolean isEmpty()集合接口的业务逻辑如下：
public interface Set<E> { void add(E e); void remove(E e); boolean contains(E e); int getSize(); boolean isEmpty();
}- 用二分搜索树作为集合的底层实现
public class BSTSet<E extends Comparable<E>> implements Set<E> { private BST<E> bst; // 构造函数
public BSTSet() {
bst = new BST<>();
} // 实现getSize方法
@Override
public int getSize() {
return bst.size();
} // 实现isEmpty方法
@Override
public boolean isEmpty() {
return bst.isEmpty();
} // 实现contains方法
@Override
public boolean contains(E e) {
return bst.contains(e);
} // 实现add方法
public void add(E e) {
bst.add(e);
} // 实现remove方法
public void remove(E e) {
bst.remove(e);
}
}- 用链表作为集合的底层实现
public class LinkedListSet<E> implements Set<E> { private LinkedList<E> list; // 构造函数
public LinkedListSet() {
list = new LinkedList<>();
} // 实现getSize方法
@Override
public int getSize() {
return list.getSize();
} // 实现isEmpty方法
@Override
public boolean isEmpty() {
return list.isEmpty();
} // 实现contains方法
@Override
public boolean contains(E e) {
return list.contains(e);
} // 实现add方法
@Override
public void add(E e) {
if (!list.contains(e)) {
list.addFirst(e);
}
} // 实现remove方法
@Override
public void remove(E e) {
list.removeElement(e);
}- 用二分搜索树实现的集合与用链表实现的集合的性能比较
import java.util.ArrayList; public class Main { public static double testSet(Set<String> set, String filename) { long startTime = System.nanoTime(); System.out.println(filename);
ArrayList<String> words = new ArrayList<>();
if (FileOperation.readFile(filename, words)) {
System.out.println("Total words: " + words.size()); for (String word : words) {
set.add(word);
}
System.out.println("Total different words: " + set.getSize());
} long endTime = System.nanoTime(); return (endTime - startTime) / 1000000000.0;
} public static void main(String[] args) {
String filename = "pride-and-prejudice.txt"; BSTSet<String> bstSet = new BSTSet<>();
double time1 = testSet(bstSet, filename);
System.out.println("BSTSet, time: " + time1 + " s"); System.out.println(); LinkedListSet<String> linkedListSet = new LinkedListSet<>();
double time2 = testSet(linkedListSet, filename);
System.out.println("LinkedListSet, time: " + time2 + " s");
}
}- 输出结果：
pride-and-prejudice.txt
Total words: 125901
Total different words: 6530
BSTSet, time: 0.109504342 s pride-and-prejudice.txt
Total words: 125901
Total different words: 6530
LinkedListSet, time: 2.208894105 s
- 通过比较结果，我们发现，用二分搜索树实现的集合的比用链表实现的集合更加高效
3.. 集合的时间复杂度分析
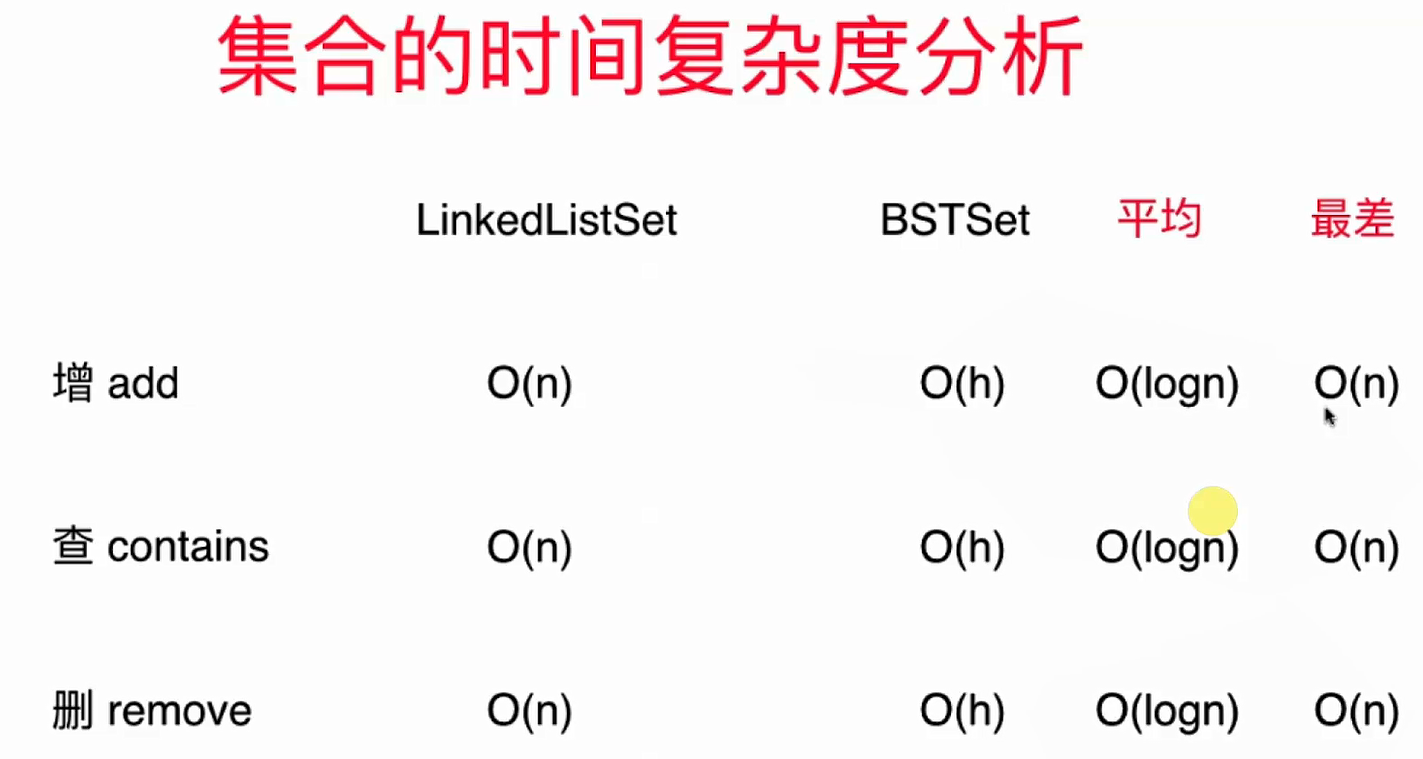
- 上图中"h"是二分搜索树的高度
- 当二分搜索树"满"的时候，性能是最佳的，时间复杂度为O(logn)；当二分搜索树退化为链表的时候，性能是最差的，时间复杂度为O(n)
4.. 映射（Map）
- 映射是存储（键，值）数据对的数据结构（Key, Value）
- 根据键（Key），寻找值（Value）
5.. 映射的实现
- 定义映射的接口
Map<K, V>
·void add(K, V)
·V remove(K)
·boolean contains(K)
·V get(K)
·void set(K, V)
·int getSize()
·boolean isEmpty()- 映射接口的业务逻辑如下
public interface Map<K, V> { void add(K key, V value); V remove(K key); boolean contains(K key); V get(K key); void set(K key, V value); int getSize(); boolean isEmpty();
}- 用链表作为映射的底层实现
public class LinkedListMap<K, V> implements Map<K, V> { private class Node {
public K key;
public V value;
public Node next; public Node(K key, V value, Node next) {
this.key = key;
this.value = value;
this.next = next;
} public Node(K key) {
this(key, null, null);
} public Node() {
this(null, null, null);
} @Override
public String toString() {
return key.toString() + " : " + value.toString();
}
} private Node dummyHead;
private int size; // 构造函数
public LinkedListMap() {
dummyHead = new Node();
size = 0;
} // 实现getSize方法
@Override
public int getSize() {
return size;
} // 实现isEmpty方法
@Override
public boolean isEmpty() {
return size == 0;
} private Node getNode(K key) {
Node cur = dummyHead;
while (cur != null) {
if (cur.key.equals(key)) {
return cur;
}
cur = cur.next;
}
return null;
} // 实现contains方法
@Override
public boolean contains(K key) {
return getNode(key) != null;
} // 实现get方法
@Override
public V get(K key) {
Node node = getNode(key); // return node == null ? null : node.value;
if (node != null) {
return node.value;
}
return null;
} // 实现add方法
public void add(K key, V value) {
Node node = getNode(key);
if (node == null) {
dummyHead.next = new Node(key, value, dummyHead.next);
size++;
} else {
node.value = value;
}
} // 实现set方法
public void set(K key, V newValue) {
Node node = getNode(key);
if (node == null) {
throw new IllegalArgumentException(key + " doesn't exist.");
} else {
node.value = newValue;
}
} // 实现remove方法
public V remove(K key) { Node node = getNode(key);
if (node == null) {
throw new IllegalArgumentException(key + " doesn't exist.");
} Node prev = dummyHead;
while (prev.next != null) {
if (prev.next.key.equals(key)) {
break;
}
prev = prev.next;
} if (prev.next != null) {
Node delNode = prev.next;
prev.next = delNode.next;
delNode.next = null;
size--;
return delNode.value;
}
return null;
}
}- 用二分搜索树作为映射的底层实现
public class BSTMap<K extends Comparable<K>, V> implements Map<K, V> { private class Node {
private K key;
private V value;
private Node left;
private Node right; // 构造函数
public Node(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
} // public Node(K key) {
// this(key, null);
// }
} private Node root;
private int size; // 构造函数
public BSTMap() {
root = null;
size = 0;
} // 实现getSize方法
@Override
public int getSize() {
return size;
} // 实现isEmpty方法
public boolean isEmpty() {
return size == 0;
} // 实现add方法
@Override
public void add(K key, V value) {
root = add(root, key, value);
} // 向以node为根节点的二分搜索树中插入元素(key, value)，递归算法
// 返回插入新元素后的二分搜索树的根
private Node add(Node node, K key, V value) { if (node == null) {
size++;
return new Node(key, value);
} if (key.compareTo(node.key) < 0) {
node.left = add(node.left, key, value);
} else if (key.compareTo(node.key) > 0) {
node.right = add(node.right, key, value);
} else {
node.value = value;
}
return node;
} // 返回以node为根节点的二分搜索树中，key所在的节点
private Node getNode(Node node, K key) { if (node == null)
return null; if (key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else if (key.compareTo(node.key) > 0) {
return getNode(node.right, key);
} else {
return node;
}
} @Override
public boolean contains(K key) {
return getNode(root, key) != null;
} @Override
public V get(K key) { Node node = getNode(root, key);
return node == null ? null : node.value;
} @Override
public void set(K key, V newValue) {
Node node = getNode(root, key);
if (node == null)
throw new IllegalArgumentException(key + " doesn't exist!"); node.value = newValue;
} // 返回以node为根的二分搜索树的最小元素所在节点
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
} // 删除掉以node为根的二分搜索树中的最小元素所在节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
} // 实现remove方法
// 删除二分搜索树中键为key的节点
@Override
public V remove(K key) {
Node node = getNode(root, key); if (node != null) {
root = remove(root, key);
return node.value;
}
return null;
} // 删除以node为根节点的二分搜索树中键为key的节点，递归算法
// 返回删除节点后新的二分搜索树的根
private Node remove(Node node, K key) {
if (node == null) {
return null;
} if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
return node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
return node;
} else {
// 待删除节点左子树为空的情况
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
// 待删除节点右子树为空的情况
} else if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
// 待删除节点左右子树均不为空
// 找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点
} else {
Node successor = minimum(node.right);
successor.right = removeMin(node.right); //这里进行了size--操作
successor.left = node.left;
node.left = null;
node.right = null;
return successor;
}
}
}
}- 用二分搜索树实现的映射与用链表实现的映射的性能比较
import java.util.ArrayList; public class Main { public static double testMap(Map<String, Integer> map, String filename) { long startTime = System.nanoTime(); System.out.println(filename);
ArrayList<String> words = new ArrayList<>();
if (FileOperation.readFile(filename, words)) {
System.out.println("Total words: " + words.size());
for (String word : words) {
if (map.contains(word)) {
map.set(word, map.get(word) + 1);
} else {
map.add(word, 1);
}
} System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
} long endTime = System.nanoTime(); return (endTime - startTime) / 1000000000.0;
} public static void main(String[] args) { String filename = "pride-and-prejudice.txt"; LinkedListMap<String, Integer> linkedListMap = new LinkedListMap<>();
double time1 = testMap(linkedListMap, filename);
System.out.println("Linked List Map, time: " + time1 + " s"); System.out.println();
System.out.println(); BSTMap<String, Integer> bstMap = new BSTMap<>();
double time2 = testMap(bstMap, filename);
System.out.println("BST Map, time: " + time2 + " s"); }
}- 输出结果
pride-and-prejudice.txt
Total words: 125901
Total different words: 6530
Frequency of PRIDE: 53
Frequency of PREJUDICE: 11
Linked List Map, time: 9.692566895 s pride-and-prejudice.txt
Total words: 125901
Total different words: 6530
Frequency of PRIDE: 53
Frequency of PREJUDICE: 11
BST Map, time: 0.085364242 s- 通过比较结果，我们发现，用二分搜索树实现的映射的比用链表实现的映射更加高效
6.. 映射的时间复杂度
- 上图中"h"是二分搜索树的高度
- 当二分搜索树"满"的时候，性能是最佳的，时间复杂度为O(logn)；当二分搜索树退化为链表的时候，性能是最差的，时间复杂度为O(n)
第二十七篇 玩转数据结构——集合（Set）与映射（Map）的更多相关文章
- 第二十三篇 玩转数据结构——栈（Stack）
1.. 栈的特点: 栈也是一种线性结构: 相比数组,栈所对应的操作是数组的子集: 栈只能从一端添加元素,也只能从这一端取出元素,这一端通常称之为"栈顶": 向栈中添加元 ...
- 第二十八篇 玩转数据结构——堆（Heap）和有优先队列(Priority Queue)
1.. 优先队列(Priority Queue) 优先队列与普通队列的区别:普通队列遵循先进先出的原则:优先队列的出队顺序与入队顺序无关,与优先级相关. 优先队列可以使用队列的接口,只是在 ...
- 第二十六篇 玩转数据结构——二分搜索树（Binary Search Tree）
1.. 二叉树 跟链表一样,二叉树也是一种动态数据结构,即,不需要在创建时指定大小. 跟链表不同的是,二叉树中的每个节点,除了要存放元素e,它还有两个指向其它节点的引用,分别用Node l ...
- 第二十五篇 玩转数据结构——链表（Linked List）
1.. 链表的重要性 我们之前实现的动态数组.栈.队列,底层都是依托静态数组,靠resize来解决固定容量的问题,而"链表"则是一种真正的动态数据结构,不需要处理固定容 ...
- 第二十四篇 玩转数据结构——队列（Queue）
1.. 队列基础 队列也是一种线性结构: 相比数组,队列所对应的操作数是队列的子集: 队列只允许从一端(队尾)添加元素,从另一端(队首)取出元素: 队列的形象化描述如下图: 队列是一种先进 ...
- 第二十九篇 玩转数据结构——线段树（Segment Tree）
1.. 线段树引入 线段树也称为区间树 为什么要使用线段树:对于某些问题,我们只关心区间(线段) 经典的线段树问题:区间染色,有一面长度为n的墙,每次选择一段墙进行染色(染色允许覆盖),问 ...
- 第二十七篇:Windows驱动中的PCI, DMA, ISR, DPC, ScatterGater, MapRegsiter, CommonBuffer, ConfigSpace
近期有些人问我PCI设备驱动的问题, 和他们交流过后, 我建议他们先看一看<<The Windows NT Device Driver Book>>这本书, 个人感觉, 这本书 ...
- 第三十一篇 玩转数据结构——并查集（Union Find）
1.. 并查集的应用场景 查看"网络"中节点的连接状态,这里的网络是广义上的网络 数学中的集合类的实现 2.. 并查集所支持的操作 对于一组数据,并查集主要支持两种操作:合并两 ...
- 第二十七篇 -- QTreeWidget总结
前言 之前写过几篇关于TreeWidget的文章,不过不方便查阅,特此重新整合作为总结.不过关于QtDesigner画图,还是不重新写了,看 第一篇 就OK. 准备工作 1. 用QtDesigner画 ...
随机推荐
- （1）-Android学习笔记之：初识Android系统架构和项目结构
Android系统架构 Android程序结构 创建一个Android项目,为初学便于理解,将程序项目结构切换为Project模式,项目结构如下 .gradle和.idea:这两个目录下放的都是And ...
- IndexedDB基本概念
控制台 IndexedDB下为数据库 数据库下为表,表内容展现为主键值和其余值,其中其余值包括索引和其他任意字段,以对象形式表现 表下为索引字段表,用来展现拥有同一种索引字段的所有数据(有多少种索引就 ...
- ZOJ1310-Robot (BFS)
The Robot Moving Institute is using a robot in their local store to transport different items. Of co ...
- Linux下搭建PHP环境的参考文章小记
之前也在Linux上安装过两次,但是当我再次需要安装时,还是很多不懂的地方,于是记下此篇,以防下次再费经心思找到不合适的文章,瞎折腾. 通过参考这几篇文章,成功的安装好了自己的PHP(LNMP)环境. ...
- MyEclipse启动Tomcat报错：Could not find the main class: org.apache.catalina.startup
问题描述 Could not find the main class:org.apache.catalina.startup.Bootstrap. Program will exit 问题原因 主要原 ...
- 【转】Java（多）线程中注入Spring的Bean
问题说明 今天在web应用中用到了Java多线程的技术来并发处理一些业务,但在执行时一直会报NullPointerException的错误,问题定位了一下发现是线程中的Spring bean没有被注入 ...
- Ecshop各个页面文件介绍，主要文件功能说明
1.模板文件说明 style.css – 模板所使用样式表activity.dwt – 活动列表article.dwt – 文章内容页article_cat.dwt – 文章列表页article_pr ...
- 动态生成sku组合输入列表
<!DOCTYPE html> <html> <head> <title></title> <meta http-equiv=&quo ...
- 3ds Max File Format (Part 2: The first inner structures; DllDirectory, ClassDirectory3)
Now that we understand the outer structure of the file, it's time to look closer to what's inside. T ...
- bash数学运算之bc
一.expr 1.1 语法 注意必须有空格 只能精确到整数,无法精确到浮点数 1.2 操作符对照表 使用expr命令时需要加\进行转义,因为部分符号是保留关键字 例1:比较num1跟num2的大小 [ ...