python排序 基数排序

算法思想

基数排序通过按位比较（一般从最低位开始）将元素按照最低位的数放到10个桶中，当所有的元素都这样被处理一次后，在按从0到9的顺序将每个桶的元素再取出来（不关注其他位的，只关注当前位的）这样就完成了所有元素最低位的有序性，然后不断的重复上面的步骤，知道所有元素的最高位都经过处理了。

算法步骤

初始化桶，共有10个，分别存放当前位位0-9的元素

从元素的最后一位开始，按照最后一位的数字将其放到相应的同元素中。对列表中的每个元素都进行上面的操作后，从0号桶开始，将元素从桶中取出来，这样就完成了一个位数的排序

重复上一过程，如果发现元素最高位已经被处理过，就把他添加到最终的结果中

算法实现

算法的主要问题在于对当前位的获取中

对于正数

(element//divisor)%10#结果是当前位上的数#divisor代表当前位，个位是1，十位是10，百位是100#//是向下取整的意思

　　如过element//divisor结果为0 就代表实际结果小于1了，即当前位已经是0了

对于负数

collection[j]//i==-1#代表是负数

　　取得当前位

(10-math.ceil(element/divisor)%10)%10#math.ceil()是向上取整
#最后一个%10是防止前面结果=10的情况出现

算法实现

def radix_sort3(collection):
    ''' 考虑是否可以将负数通过abs转为正数来判断
        外层循环控制进位，即先排最低位的，然后排倒数第二位的..一直处理到每个元素的最高位 ，最高为处理后，放到最终结果集中
        内层循环控制数组元素的遍历
        对每个数组元素，首先分大于0和小于0的两种情况，因为涉及到正数和负数的寻找最低位数字的算法逻辑大小不一样
        对正数来说，分为当前进位后还有元素此时放到临时变量中，当前进位就是最后一位此时就放到最终的结果集中，相应的判断逻辑解释见版本0
        负数也和上面差不多
        在内层for结束以后，还需要将临时变量中的元素给取出来'''
    result_negative=[]
    result_positive=[]
    divisor=[pow(10,i) for i in range(10)]
    for i in divisor:
        bucket=[[] for j in range(10)]
        if len(collection)==0:
            break
        for j in range(len(collection)):
            if collection[j]//i>0:
                bucket[(collection[j]//i)%10].append(collection[j])
                continue
            elif collection[j]//i==0:
                result_positive.append(collection[j])
                continue
            #负数的
            # elif collection[j]//i<-1:
            #     bucket[(10-math.ceil(collection[j]/i)%10)%10].append(collection[j])
            #     continue
            # elif collection[j]//i==-1:#会出现bug，-100/100=-1，然后就被放到了最终结果中，但其实不应该被这样的
            #     if math.ceil(collection[j]/i)==-1:
            #         bucket[(10-math.ceil(collection[j]/i)%10)%10].append(collection[j])
            #         continue
            #     result_negative.insert(0,collection[j])
            #     continue
        collection=[]
        for k in bucket:
            if k:
                collection.extend(k)
    return result_negative+result_positive

效率分析

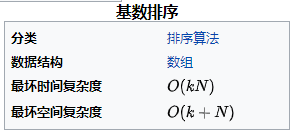
时间复杂度：进行k次关于数位的循环，每次循环里还有一个循环，要对N个元素进行放桶，一共循环kN

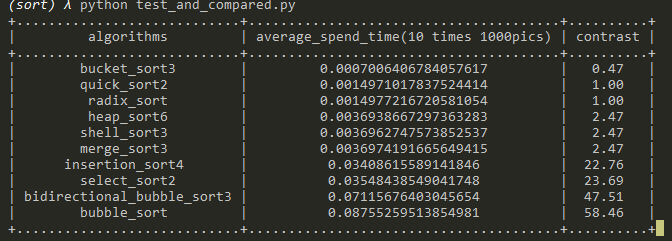
对比