长乐国庆集训Day4

T1 一道数论神题

题目

【题目描述】

LYK有一张无向图G={V,E}，这张无向图有n个点m条边组成。并且这是一张带权图，只有点权。

LYK想把这个图删干净，它的方法是这样的。每次选择一个点，将它删掉，但删这个点是需要代价的。

假设与这个点相连的还没被删掉的点是u₁,u₂,…,u_k。LYK将会增加 a[u₁],a[u₂],…,a[u_k]的疲劳值。

它想将所有点都删掉，并且删完后自己的疲劳值之和最小。你能帮帮它吗？

【输入格式】

第一行两个数n,m表示一张n个点m条边的图。

第二行n个数a_i表示点权。

接下来m行每行三个数u,v，表示有一条连接u,v的边。数据保证任意两个点之间最多一条边相连，并且不存在自环。

【输出格式】

你需要输出这个最小疲劳值是多少。

【输入样例】

【输出样例】

【数据规模】

对于30%的数据n≤10。

对于60%的数据n,m≤1000。

对于 100%的数据1≤n,m,a_i≤100000。

解析

久违的送分题

贪心思想，将每个点对与其连接的点的贡献从大到小排序，依次删除即可。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <vector>

#include <cmath>

using namespace std;

inline int read()

{

    int num=;

    char ch=getchar();

    while(ch<''||ch>'') ch=getchar();

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num;

}

const int N=;

struct rec{

    int w,num;

}a[N];

int n,m,b[N];

long long ans;

bool v[N];

vector<int> edge[N];

bool cmp(rec x,rec y)

{

    return x.w>y.w;

}

int main()

{

    //freopen("god.in","r",stdin);

    //freopen("god.out","w",stdout);

    memset(v,false,sizeof(v));

    n=read(),m=read();

    for(int i=;i<=n;i++) a[i].w=read(),a[i].num=i,b[i]=a[i].w;

    for(int i=;i<=m;i++)

    {

        int x=read(),y=read();

        edge[x].push_back(y),edge[y].push_back(x);

    }

    sort(a+,a+n+,cmp);

    for(int i=;i<=n;i++)

    {

        int x=a[i].num;

        v[x]=true;

        for(int j=;j<edge[x].size();j++)

            if(!v[edge[x][j]]) ans+=b[edge[x][j]];

    }

    cout<<ans;

    return ;

}

T2 数组异或

题目

【题目描述】

xor——异或，和and与or一样，是一种重要的逻辑运算，他的运算规律是0xor 0=0，1 xor 1=0，1 xor 0=1，0 xor 1=1。

两个整数之间的异或是将两个整数转化成二进制，对他们的每一位分别进行xor操作，例：6(110) xor 13(1101) = 11(1011)

现在我们要介绍一种新的操作——数组异或，将两个相同大小（假设都为n）的数组A、B异或成一个新数组C，则新数组必满足:

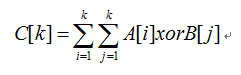
现在给你数组大小n，和两个数组A,B

求他们的异或数组C

由于最终答案可能过大，你需要对C的每个元素对10⁹+7取模

【输入格式】

一共3行。

第一行一个正整数N。

接下来两行每行N个正整数，表示数组A、B。

【输出格式】

一共1行，N个正整数，表示数组C。

【输入样例】

【输出样例】

【数据规模】

对于50%的数据，N≤100。

对于全部的数据，N≤10⁵。

解析

数论不太懂，以下是出题人的题解。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

inline int read()

{

    int num=;

    char ch=getchar();

    while(ch<''||ch>'') ch=getchar();

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num;

}

const int N=,mod=;

int n,a[N],b[N],aa[][],bb[][];

int main()

{

    //freopen("xorarray.in","r",stdin);

    //freopen("xorarray.out","w",stdout);

    n=read();

    for(int i=;i<=n;i++) a[i]=read();

    for(int i=;i<=n;i++) b[i]=read();

    for(int i=;i<=n;i++)

    {

        long long c=;

        for(int j=;j<=;j++)

        {

            aa[j][(a[i]>>j)&]++,bb[j][(b[i]>>j)&]++;

            long long cc=((long long)aa[j][]*bb[j][]+(long long)aa[j][]*bb[j][])%mod*(<<j)%mod;

            c=(c+cc)%mod;

        }

        cout<<c<<" ";

    }

    return ;

}

T3 侦探游戏

题目

【题目描述】

小W最近沉迷一个侦探游戏，在这个游戏中会不断出现命案，而小W作为主角，需要不断地收集各种关键证据，只有当所有的关键证据都被找到，你才能驳倒所有人错误的判断，找出真正的凶手。

一共有N个关键证据以及M条信息，每条信息如下所示 : 如果你已经掌握了证据i，那么你可以通过k个时间的搜索和推理得到证据j，同样的，如果你掌握了证据j你也可以通过k个时间得到证据i。

游戏开始时玩家通过初步观察现场已经得到了证据1，于此同时，每个玩家在游戏开始阶段时都能获得一个特殊技能来加快游戏进度，增加趣味性。小W 选了一个他以前从来没用过的技能:好运。这是一个被动技能，系统会在游戏开始时选定一对证据(a,b)（a≠b）当小W发现其中一个证据的时候，他会很好运地立即获得另外一个证据（不计入时间）。

但是这个技能是完全随机的，小W完全不知道进入游戏后系统会挑选哪一对证据，他希望你能帮助他算出他花在本轮游戏上的时间的期望值，这样他心里能有点B数。

提供的信息保证: i不会等于j，每个k值都互不相同，N个证据都能被得到。

【输入格式】

一共M+1行。

第一行两个正整数N和M，表示证据数量和信息数量。

接下来M行，每行三个数字i,j,k表示一个信息

【输出格式】

共1行，1个整数（期望值是实数，但这里请直接保留2位小数输出）。

【输入样例】

【输出样例】

2.33

【数据规模】

对于20%的数据，N≤100

对于60%的数据，N≤1000

对于全部的数据，N≤20000，M≤10⁵，1≤k≤10⁶。

解析

一条边权为w的边，如果把MST上所有边权小于w的边加入，且该边加入后联通的点对数增加了K，那么路径上最大边权为w的点对数即为K。

所以可以用一个并查集，把边权从小到大加边，对于边(u,v,w)，答案累加size_u*size_v*w，再合并u,v两点所属联通块。(size_i表示点i所属联通块的大小)。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

inline int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

const int N=,M=;

struct rec{

    int u,v,d;

}edge[M];

int n,m,fa[N],s[N];

long long cnt,sum;

bool cmp(rec x,rec y)

{

    return x.d<y.d;

}

int find(int x)

{

    if(fa[x]==x) return fa[x];

    return fa[x]=find(fa[x]);

}

int main()

{

    n=read(),m=read();

    for(int i=;i<=m;i++) edge[i].u=read(),edge[i].v=read(),edge[i].d=read();

    sort(edge+,edge+m+,cmp);

    for(int i=;i<=n;i++) fa[i]=i,s[i]=;

    for(int i=;i<=m;i++)

    {

        int x=find(edge[i].u),y=find(edge[i].v);

        if(x==y) continue;

        sum+=edge[i].d,cnt+=(long long)s[x]*s[y]*edge[i].d,s[x]+=s[y],fa[y]=x;

    }

    double ans=sum-2.0*cnt/n/(n-);

    printf("%.2lf",ans);

    return ;

}

T4 天上掉馅饼

题目

【题目描述】

小G进入了一个神奇的世界，在这个世界，天上会掉下一些馅饼。今天，天上会随机掉下k个馅饼。

每次天上掉下馅饼，小 G 可以选择吃或者不吃（必须在下一个馅饼掉下来之前作出选择，并且现在决定不吃的话以后也不能吃）。

馅饼有n种不同的馅，根据物理定律，天上掉下这n种馅饼的概率相同且相互独立。然而，每一种馅饼i都有一个前提馅饼集合S_i。只有当S_i中的馅饼都吃过之后，才能吃第i 种馅饼。比如说，韭菜馅馅饼的S中有白菜猪肉馅饼和鲜虾馅饼，那么小G只有在吃过白菜猪肉馅饼和鲜虾馅饼之后，才能吃韭菜馅的馅饼。

同时，每个馅饼还有一个美味值P_i。今天一天小G的幸福度，等于小G吃到的所有馅饼的美味值之和。注意：Pi 可能是负数。

现在考虑，采用最优策略的前提下，小G这一天期望的幸福度是多少？

【输入格式】

第一行两个正整数k和n，表示馅饼的数量和种类。

以下n行，每行若干个数，描述一种馅饼。其中第一个数代表美味值，随后的整数表示该馅饼的前提馅饼，以0结尾。

【输出格式】

输出一个实数，保留6位小数，即在最优策略下期望的幸福度。

【输入样例】

【输出样例】

1.500000

【数据规模】

对于20%的数据，所有的馅饼都没有“前提馅饼”。

对于50%的数据，1≤k≤10，1≤n≤10。

对于100%的数据，1≤k ≤100，1≤ n≤15，美味度为[-10⁶,10⁶]的整数。

解析

n只有15，显然状压DP，令f[i][j]表示在第1轮到第i-1轮内是否取过状态为j的最大期望得分。

则状态转移方程为：（1≤k≤n）

j状态满足吃第k种馅饼的条件，则不吃为f[i+1][j]，吃则为f[i+1][j|(1<<k-1)]+P_k，取两者最大值累加f[i][j]即可；
j状态不满足吃第k种馅饼的条件，则不能吃，即f[i][j]=f[i+1][j]。

至于期望值，虽然很高端的样子，但实际上，由于f[i][j]覆盖了第i轮吃n种馅饼的情况，所以对于每个f[i][j]，均除以n即可。

答案即为f[1][0]。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

inline int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

const int N=,K=,T=<<;

int k,n,v[N],d[N];

double f[K][T];

int main()

{

    k=read(),n=read();

    for(int i=;i<=n;i++)

    {

        v[i]=read();

        int x=read();

        while(x) d[i]+=<<(x-),x=read();

    }

    for(int i=k;i>=;i--)

        for(int j=;j<<<n;j++)

        {

            for(int p=;p<=n;p++)

                if((j&d[p])==d[p]) f[i][j]+=max(f[i+][j],f[i+][j|(<<(p-))]+v[p]);

                else f[i][j]+=f[i+][j];

            f[i][j]/=n;

        }

    printf("%.6f",f[][]);

    return ;

}