Docker02-重要概念

Docker简介
虚拟化和Docker的对比
Docker的架构

Docker简介

思考

思考一：
我们之前是如何将项目发布到Linux服务器的？
大致步骤如下

安装jdk
安装tomcat
将项目war包上传到tomcat的webapps下
修改配置文件
启动tomcat

这样看似没问题，其实我们想想，发一台机器还好，这几步就完成了。如果我们要将这个项目发布到N多台机器，那么我们是否需要再每个机器上都进行相同的步骤？并且要进行环境兼容性的测试。

思考二：
再来看一个例子，我们现在是想部署一个成熟的产品，这个产品是go语言开发的，我们该如何部署？go语言运行的环境怎么装，这个项目又该如何部署？

思考三：
一台linux机器上装了很多软件，部署了很多项目，相互之间有干扰怎么办？

Docker是什么

Docker是以容器技术为核心的一套应用的构建，分发，执行的体系和生态。

Docker 解决了什么问题

程序在我这里跑的好好的，在你那怎么不行了？（环境与程序打包交付）
系统好卡，是哪个进程把CPU吃光了？（容器之间沙箱隔离）
这套系统我已经搭建好了，要不你再重新搭一遍？（一次构建，到处运行）

Docker 的优点

更快速的交付和部署
对开发和运维来说，最希望的是一次构建或配置，可以在任意地方正常运行。
例如：开发者可以使用一个标准的镜像来构建一套开发容器，开发完成之后，运维人员可以直接使用这个容器来部署代码。Docker容器很轻很快，容器的启动时间是秒级的，大量地节约开发，测试，部署的时间，并且解决开发环境和生产环境不一致的问题。
更轻松的迁移和扩展
Docker容器几乎可以在任意的平台上运行，包括物理机、虚拟机、公有云、私有云、个人电脑、服务器等，这种兼容性可以让用户把一个应用程序从一个平台直接迁移到另外一个平台。
更高的资源利用率
Docker对系统资源的利用率很高，一台主机上可以同时运行数千个Docker容器，容器除了运行其中的应用外，基本不消耗额外的系统资源，使得应用的性能很高，同时系统的开销尽量小。

Docker的目的

集装箱：变革了人类整个的生产流程体系，让货物全世界流通
Docker：变革了IT领域的软件交付方式，让IT之间的鸿沟消失

:-: 目标：简化部署流程，提高生产力

Docker常用场景

构建DevOps流程，实现运维的自动化
企业私有的PAAS平台，降低开发成本，提升效率
企业级AppStore，统一的后端系统分发平台
间歇式计算任务
构建微服务架构

虚拟化和Docker的对比

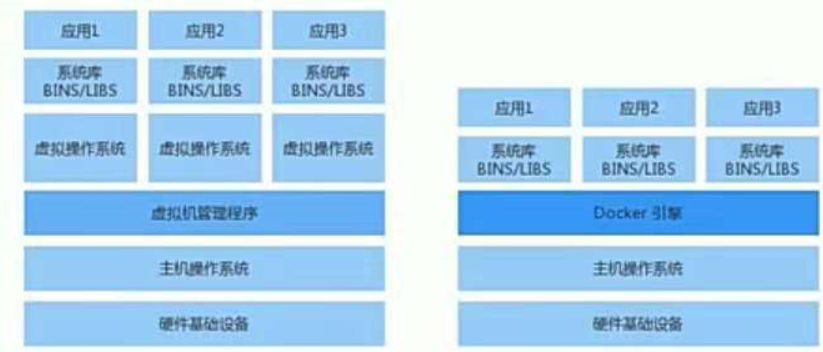
Docker的架构

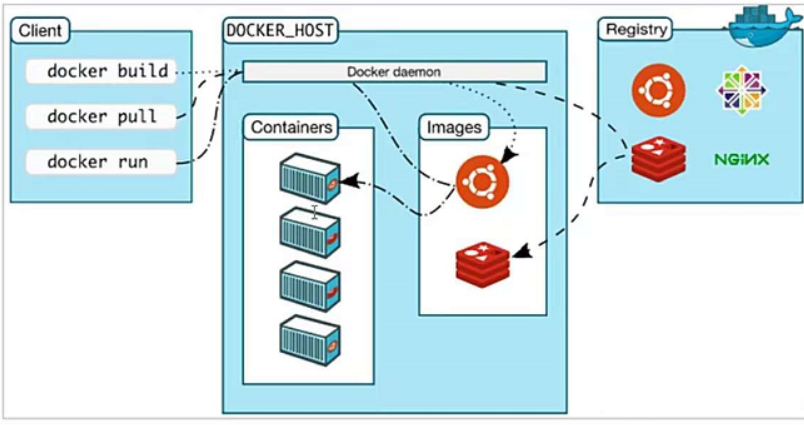
Docker daemon(Docker 进程)
Docker进程是部署在linux操作系统上，负责支撑Docker Container（容器）的运行以及本地Image（镜像）的管理。

Docker Client
用户不直接操作Docker daemon，用户通过Docker client访问Docker，Docker client提供pull,build,run等操作命令。

Docker Images
Docker 镜像，就是一个只读的模板。
例如一个镜像可以包含一个完整的linux操作系统环境，里面安装了用户需要的应用程序。
镜像可以用来创建Docker容器。Docker 提供了一个很简单的机制来创建镜像或者更新现有的镜像，用户甚至可以从其他人那里下载一个已经做好的镜像来直接使用。

Docker Containers
Docker 容器，是镜像的一个运行实例。
Docker 是利用容器来运行应用的，它可以被启动、开始、停止、删除。每个容器都是互相隔离的，保证安全的平台。可以把容器看做是一个简易版的linux环境和运行在其中的应用程序。

Docker Registry
仓库分为公开仓库和私有仓库两种形式。
最大的公开仓库是 Docker Hub，存放了数量庞大的镜像供用户下载;用户也可以在本地网络内创建一个私有仓库。
当用户创建了自己的镜像之后就可以使用push命令将它上传到公有或私有仓库，这样其他人只需要从仓库上pull下来就可以了。

:-:
微信扫一扫，关注“python测试开发圈”，了解更多测试教程！