Codeforces 839D Winter is here - 暴力 - 容斥原理

Winter is here at the North and the White Walkers are close. John Snow has an army consisting of n soldiers. While the rest of the world is fighting for the Iron Throne, he is going to get ready for the attack of the White Walkers.

He has created a method to know how strong his army is. Let the i-th soldier’s strength be ai. For some k he calls i1, i2, ..., ik a clan if i1 < i2 < i3 < ... < ik and gcd(ai1, ai2, ..., aik) > 1 . He calls the strength of that clan k·gcd(ai1, ai2, ..., aik). Then he defines the strength of his army by the sum of strengths of all possible clans.

Your task is to find the strength of his army. As the number may be very large, you have to print it modulo 1000000007 (109 + 7).

Greatest common divisor (gcd) of a sequence of integers is the maximum possible integer so that each element of the sequence is divisible by it.

Input

The first line contains integer n (1 ≤ n ≤ 200000) — the size of the army.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 1000000) — denoting the strengths of his soldiers.

Output

Print one integer — the strength of John Snow's army modulo 1000000007 (109 + 7).

Examples

input

3
3 3 1

output

12

input

4
2 3 4 6

output

39

Note

In the first sample the clans are {1}, {2}, {1, 2} so the answer will be 1·3 + 1·3 + 2·3 = 12

---

　　题目大意 给定n，集合A，设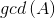表示把这个集合内的所有数求最大公约数的结果，求。

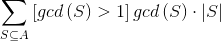　　根据常用套路，套一个循环去枚举gcd的结果，然后再求系数，于是有

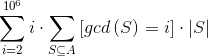
　　现在设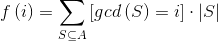,于是有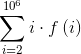

　　现在考虑求f(i)。可以想到容斥原理。

　　先假设所有的集合的gcd是i的倍数都符合条件然后计算答案(给定数集A中所有是i的倍数的数组成的集合任选一个子集)，然后再减去f(2i), f(3i)，...

　　现在要面临两个问题

1. 第一次求值如何处理？
   首先把式子写出来，设这个集合的大小为n，那么有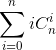

   因为

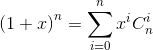
   对两边同时进行求导得到

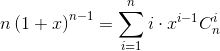
   再带入x = 1得到

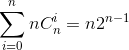
2. 设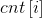为是i的倍数的数的个数，如何快速求出?

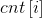   根据定义式有

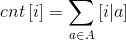
   显然超时。虽然这是暴力，但是不够优美。
   设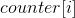表示，集合A中恰好为i的数有多少个。

   然后就可以得到总时间复杂度为O(mlog₂m)的暴力:

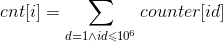
　　最后求求和就完事了。

Code

 /**
  * Codeforces
  * Problem#839D
  * Accepted
  * Time: 171ms
  * Memory: 15400k
  */
 #include <bits/stdc++.h>
 using namespace std;

 const int lim = 1e6 + ;
 const int moder = 1e9 + ;

 int n;
 int *a;
 int *pow2;
 int cnt[lim], counter[lim];
 int f[lim];
 int res = ;

 inline void init() {
     scanf("%d", &n);
     a = new int[(n + )];
     pow2 = new int[(n + )];
     pow2[] = ;
     for(int i = ; i <= n; i++) {
         scanf("%d", a + i);
         counter[a[i]]++;
         pow2[i] = (pow2[i - ] << ) % moder;
     }
 }

 inline void solve() {
     for(int i = ; i < lim; i++)
         for(int j = i; j < lim; j += i)
             cnt[i] += counter[j];

     for(int i = lim - ; i > ; i--) {
         if(!cnt[i])    continue;
         f[i] = (cnt[i] * 1LL * pow2[cnt[i] - ]) % moder;
         for(int j = i << ; j < lim; j += i)
             f[i] = (f[i] - f[j]) % moder;
         if(f[i] < )    f[i] += moder;
         res = (res + (f[i] * 1LL * i) % moder) % moder;
     }

     printf("%d\n", res);
 }

 int main() {
     init();
     solve();
     return ;
 }

更新日志

• 2017-11-30 更新两处指数错误