乘法器——Wallace树型乘法器

博主最近在看乘法器相关的知识，发现现在用的比较多的是booth编码的乘法器和Wallace树型乘法器，当然两者并不是互斥的关系，他们也可以结合使用。在这里给大家介绍一下Wallace树型乘法器，希望能对大家有所帮助。

首先我们以两个无符号8位二进制数相乘为例来说明Wallace树的算法。由图1所示，图中8位二进制数a和8位二进制数b相乘，产生64个乘积项，记做a[i]*b[j]，i,j=0、1、2、3、4、5、6、7，在本文中，乘号用*来表示，在图中也将a[i]*b[j]用*表示。处在同一列的所有乘积项与从右边过来的进位相加，得到乘积的一位结果，由于64个乘积项可以用64个与门同时得到，即a*b=a&b，我们可以用多个全加器对处在同一列的乘积项同时相加。

　　一个全加器有三位输入和两位输出，其中一个输出为加法结果（sum），另一个输出为进位（cout）。图中一个长方形代表一个全加器，内部有两个*的长方形可以用半加器实现，圆圈中的单个乘积暂时不做处理，送入下一级参与运算。这样即实现了3-2压缩，因为全加器是3输入2输出的。

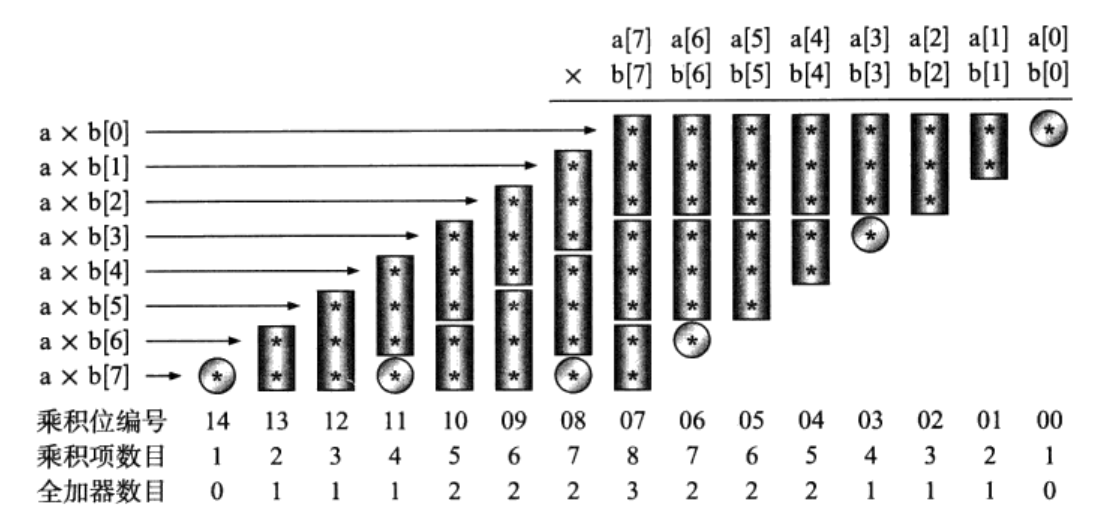
图1 8*8Wallace树型乘法器乘积项

　　图2表示了第07位的运算情况，07位有8个乘积项，他们分别是a[7]*b[0]、a[6]*b[1]、a[5]*b[2]、a[4]*b[3]、a[3]*b[4]、a[2]*b[5]、a[1]*b[6]、a[0]*b[7]，每一项a和b的[]中的数字之和为7。

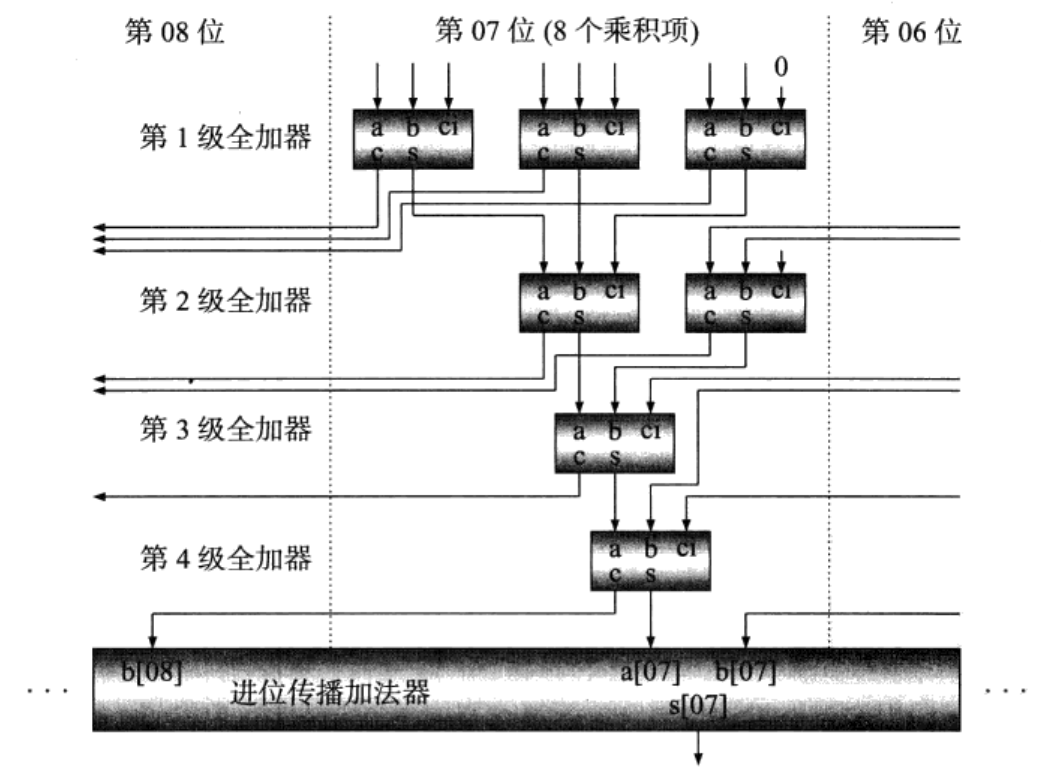图2 8*8Wallace树型乘法器第07位

在第一级，我们使用3个全加器，产生3位相加结果与3位进位。3位进位送到左边的第08位。第二级有5位相加，其中3位来自第一级，两位是来自右边06位的进位，第二级使用了两个全加器。第三级和第四级都使用了1个全加器，由于每一级各自的全加器是并行的，故每一级的延迟只相当于一个全加器的延迟，我们把第四级的输出分成sum和cout两组，再把它们用进位传播加法器相加，得到最后的结果，即乘积。

图三所示为8*8Wallace树型乘法器总体电路图，图中第一行数字是乘积位的编号，第二行数字是相应位的乘积项数量。加法器的数字是该加法器名称的右半部分，左半部分在图中的最左侧给出。如左下角最后一个加法器的名称为fal_14_0。

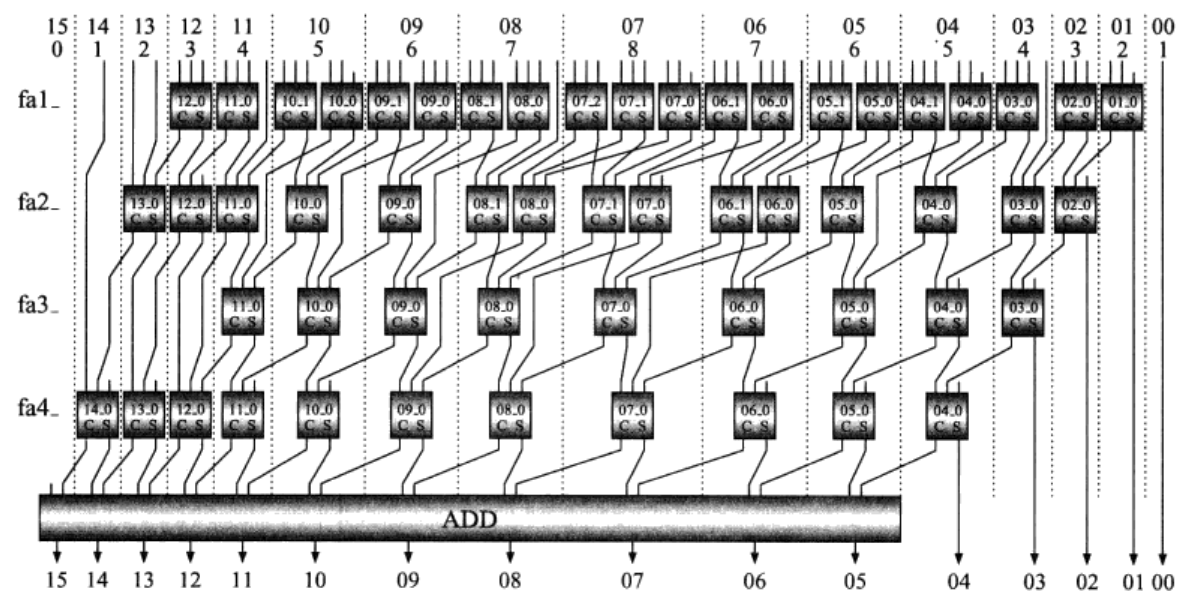
图3 8*8Wallace树型乘法器总体电路图

以上就是Wallace树型加法器的基本原理。