noip杂题题解

---

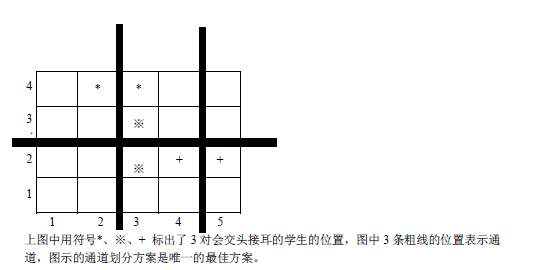
　　这道题没有什么可说的，先统计，然后几次快排，答案就出来了

Code（整齐但不简洁的代码）

 #include<iostream>
 #include<cstdio>
 #include<fstream>
 #include<cstring>
 #include<queue>
 #include<algorithm>
 using namespace std;
 typedef bool boolean;
 template<typename T>
 inline void readInteger(T& u){
     char x;
     while(!isdigit((x = getchar())));
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
 }
 int m, n;
 int k, l;
 int d;
 typedef class Point{
     public:
         int x;
         int y;
         Point(const int x = , const int y = ):x(x), y(y){}
         boolean operator <(Point another) const{
             if(this->x != another.x)    return this->x < another.x;
             return this->y < another.y;
         }
 }Point;
 inline Point readPoint(){
     Point a;
     readInteger(a.x);
     readInteger(a.y);
     return a;
 }
 typedef class MyData{
     public:
         int num;
         int count;
         MyData(const int num = ):num(num){}
 }MyDatas;
 MyData *c_r;
 MyData *c_l;
 inline void init(){
     readInteger(m);
     readInteger(n);
     readInteger(k);
     readInteger(l);
     readInteger(d);
     c_r = new MyData[(const int)(m + )];
     c_l = new MyData[(const int)(n + )];
     memset(c_r, , sizeof(MyData) * (m + ));
     memset(c_l, , sizeof(MyData) * (n + ));
     for(int i = ; i <= m; i++)    c_r[i].num = i;
     for(int i = ; i <= n; i++) 　　c_l[i].num = i;
     for(int i = ; i <= d; i++){
         Point a = readPoint();
         Point b = readPoint();
         Point s = min(a, b);
         if(a.x == b.x){
             c_l[s.y].count++;
         }else c_r[s.x].count++;
     }
 }
 boolean cmpare(const MyData &a, const MyData &b){
     return a.count > b.count;
 }
 boolean cmpare2(const MyData &a, const MyData &b){
     return a.num < b.num;
 }
 inline void solve(){
     sort(c_l + , c_l + n + , cmpare);
     sort(c_r + , c_r + m + , cmpare);
     sort(c_l + , c_l + l + , cmpare2);
     sort(c_r + , c_r + k + , cmpare2);
     for(int i = ; i <= k; i++){
         printf("%d ", c_r[i].num);
     }
     putchar('\n');
     for(int i = ; i <= l; i++){
         printf("%d ", c_l[i].num);
     }
 }
 int main(){
     freopen("seat.in", "r", stdin);
     freopen("seat.out", "w", stdout);
     init();
     solve();
     return ;
 }

---

---

　　这道题是有依赖的背包问题的裸题，一个主件最多有两个附件，而且附件没有属自己的附件，所以不用考虑树形dp

直接用普通的dp就行了，考虑4个状态

　　1）只要主件

　　2）只要主件和第一个附件

　　3）只要主件和第二个附件

　　4）要主件和它的两个附件

　　如果某个主件的第二个附件不存在呢？不管，不会影响答案，如果特判的话很耗代码。

　　如果dp到附件怎么办？不管，直接跳过

　　如果你希望运行的速度更快，可以将n和每个v除以10，最后结果乘上10

Code（极其不简洁的代码）

 #include<iostream>
 #include<cstdio>
 #include<fstream>
 #include<cstring>
 #include<queue>
 #include<algorithm>
 using namespace std;
 ///template starts
 typedef bool boolean;
 template<typename T>
 inline void readInteger(T& u){
     char x;
     while(!isdigit((x = getchar())));
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
 }
 ///template ends
 int n;
 int m;
 int *v;
 int *w;
 int *son[];
 int f[];
 int result;
 boolean *seced;
 inline void init(){
     readInteger(n);
     readInteger(m);
     n /= ;
     v = new int[(const int)(m + )];
     w = new int[(const int)(m + )];
     son[] = new int[(const int)(m + )];
     son[] = new int[(const int)(m + )];
     seced = new boolean[(const int)(m + )];
     memset(seced, false, sizeof(boolean) * (m + ));
     memset(son[], , sizeof(int) * (m + ));
     memset(son[], , sizeof(int) * (m + ));
     for(int i = , a; i <= m; i++){
         readInteger(v[i]);
         v[i] /= ;
         readInteger(w[i]);
         readInteger(a);
         if(a == )    seced[i] = true;
         if(son[][a] == )    son[][a] = i;
         else son[][a] = i;
     }
 }
 inline void solve(){
     seced[] = true;
     v[] = w[] = ;
     for(int i = ; i <= m; i++){
         if(seced[i]){
             for(int j = n; j >= v[i]; j--){
                 f[j] = max(f[j - v[i]] + v[i] * w[i], f[j]);
                 int s = ;
                 int sv = ;
                 for(int k = ; k < ; k++){
                     int r = v[son[k][i]] * w[son[k][i]];
                     s += r;
                     sv += v[son[k][i]];
                     if(j >= v[i] + v[son[k][i]]){
                         f[j] = max(f[j - v[i] - v[son[k][i]]] + v[i] * w[i] + r, f[j]);
                     }
                 }
                 if(j >= v[i] + sv){
                     f[j] = max(f[j - v[i] - sv] + v[i] * w[i] + s, f[j]);
                 }
             }
         }
     }
     printf("%d", f[n] * );
 }
 int main(){
     freopen("budget.in", "r", stdin);
     freopen("budget.out", "w", stdout);
     init();
     solve();
     return ;
 }

---

---

　　这题有两个比较常见的做法，我只写其中一个，但还是都说说

1）Tarjan + 拓扑

　　首先用Tarjan将所有的环（强连通分量）求出来，缩成一个点，求出它的最大值和最小值

接着从起点开始，进行拓扑排序，求出答案

2）spfa

　　首先可以枚举一个断点，为了使答案最大，所以从起点到断点找到一个最小值，再从终点

到起点找到一个最大值，在这个最小值这个点买入，在最大值这个点卖出，用最大值减最小值

求出这个差价。

　　如果每个断点都去跑两次spfa肯定会超时，所以就先用两次spfa预处理，第一次spfa在原

先的图上求出从起点出发，到i这个点的最短“距”，再从反向图中，从终点开始求出到点i这个点

的最长“距”

Code（比较复杂的代码）

 #include<iostream>
 #include<cstdio>
 #include<fstream>
 #include<cstring>
 #include<queue>
 #include<algorithm>
 using namespace std;
 ///template starts
 typedef bool boolean;
 template<typename T>
 inline void readInteger(T& u){
     char x;
     while(!isdigit((x = getchar())));
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
 }
 typedef class Edge{
     public:
         int end;
         int next;
         Edge(const int end = , const int next = ):end(end), next(next){}
 }Edge;
 typedef class MapManager{
     public:
         int ce;
         int *h;
         Edge *edge;
         MapManager():ce(), h(NULL), edge(NULL){}
         MapManager(int limit, int points):ce(){
             h = new int[(const int)(points + )];
             edge = new Edge[(const int)(limit + )];
             memset(h, , sizeof(int) * (points + ));
         }
         inline void addEdge(int from, int end){
             edge[++ce] = Edge(end, h[from]);
             h[from] = ce;
         }
 }MapManager;
 ///template ends
 int n, m;
 int getData(boolean (*cmpare)(const int&, const int&), int a, int b){
     if((*cmpare)(a, b))    return a;
     return b;
 }
 int *prices;
 inline void spfa(MapManager& g, int start, int end, int *f, boolean* visited, boolean (*cmpare)(const int&, const int&)){
     memset(visited, false, sizeof(boolean) * (n + ));
     queue<int> que;
     que.push(start);
     visited[start] = true;
     while(!que.empty()){
         int u = que.front();
         que.pop();
         visited[u] = false;
         for(int i = g.h[u]; i != ; i = g.edge[i].next){
             int eu = g.edge[i].end;
             int d = getData(cmpare, f[u], prices[eu]);
             if((*cmpare)(d, f[eu])){
                 f[eu] = d;
                 if(!visited[eu]){
                     que.push(eu);
                     visited[eu] = true;
                 }
             }
         }
     }
 }
 MapManager g;
 MapManager rev_g;
 int *maxdis;
 int *mindis;
 boolean *visited;
 boolean _min(const int &a, const int &b){    return a < b;    }
 boolean _max(const int &a, const int &b){    return a > b;    }
 inline void init(){
     readInteger(n);
     readInteger(m);
     g = MapManager(m * , n);
     rev_g = MapManager(m * , n);
     prices = new int[(const int)(n + )];
     maxdis = new int[(const int)(n + )];
     mindis = new int[(const int)(n + )];
     visited = new boolean[(const int)(n + )];
     memset(maxdis, , sizeof(int) * (n + ));
     memset(mindis, 0x7f, sizeof(int) * (n + ));
     for(int i = ; i <= n; i++)
         readInteger(prices[i]);
     for(int i = , a, b, c; i <= m; i++){
         readInteger(a);
         readInteger(b);
         readInteger(c);
         g.addEdge(a, b);
         rev_g.addEdge(b, a);
         if(c == ){
             g.addEdge(b, a);
             rev_g.addEdge(a, b);
         }
     }
 }
 inline void solve(){
     spfa(g, , n, mindis, visited, _min);
     spfa(rev_g, n, , maxdis, visited, _max);
     int result = ;
     for(int i = ; i < n; i++){
         result = max(result, maxdis[i] - mindis[i]);
     }
     printf("%d", result);
 }
 int main(){
     freopen("trade.in", "r", stdin);
     freopen("trade.out", "w", stdout);
     init();
     solve();
     return ;
 }

（ps：为了防止写两遍spfa，所以一次spfa写得比较复杂）