动态规划模板1|LIS最长上升子序列

LIS最长上升子序列

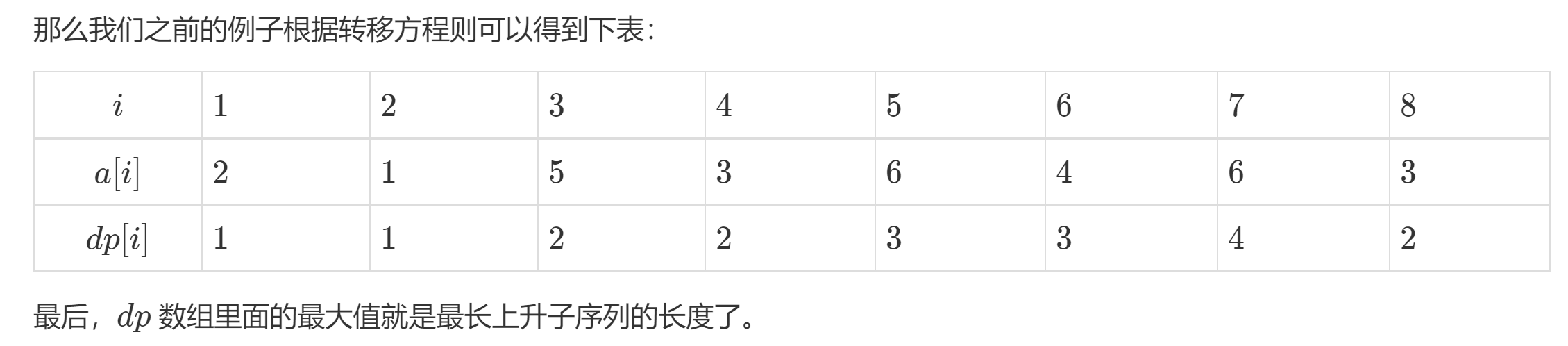
dp[i]保存的是当前到下标为止的最长上升子序列的长度。

模板代码：

int dp[MAX_N], a[MAX_N], n;
int ans = 0;  // 保存最大值

for (int i = 1; i <= n; ++i) {
    dp[i] = 1;
    for (int j = 1; j < i; ++j) {
        if (a[j] < a[i]) {
            dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    ans = max(ans, dp[i]);
}

cout << ans << endl;  // ans 就是最终结果

二分优化LIS

复杂度O(nlongn)

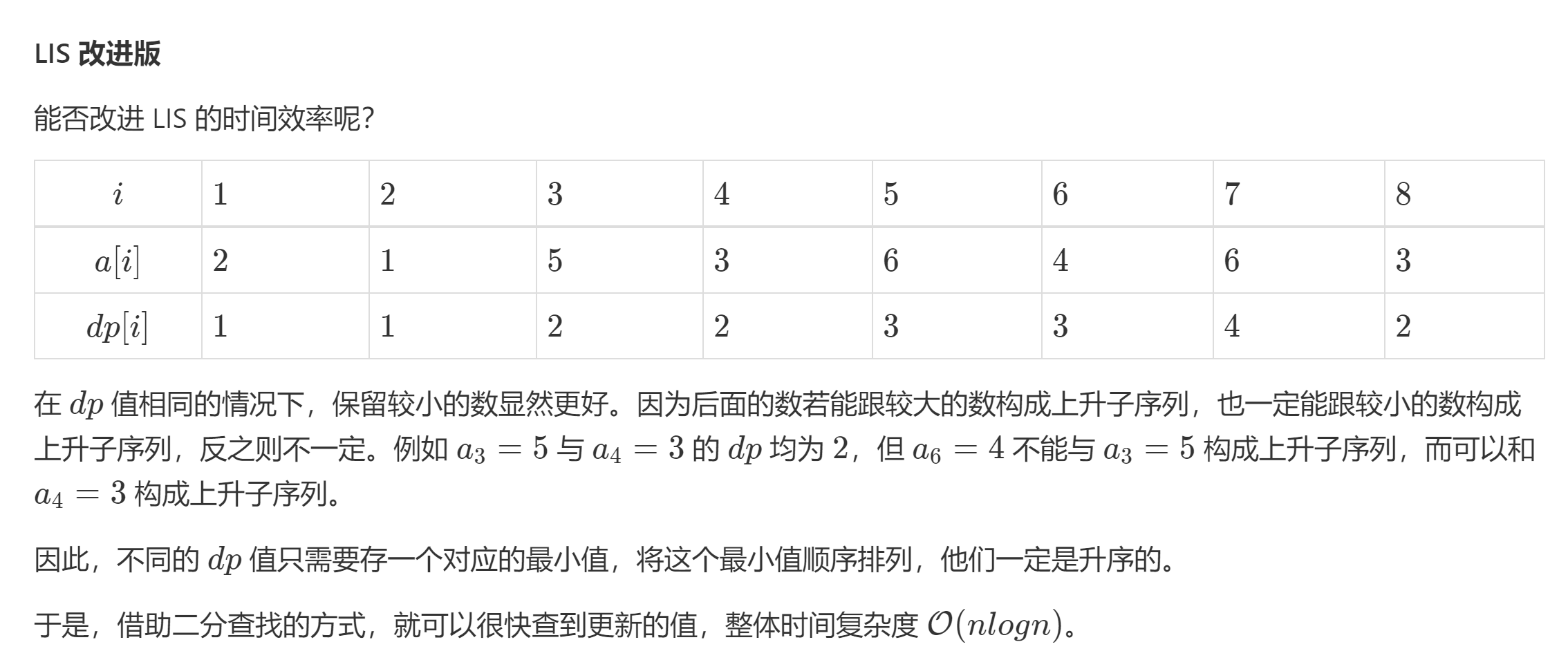
int ans[MAX_N], a[MAX_N], dp[MAX_N], n;  // ans 用来保存每个 dp 值对应的最小值，a 是原数组
int len; // LIS 最大值

ans[1] = a[1];
len = 1;

for (int i = 2; i <= n; ++i) {
    if (a[i] > ans[len]) {
        ans[++len] = a[i];
    } else {
        int pos = lower_bound(ans + 1, ans + len + 1, a[i]) - ans;
        ans[pos] = a[i];
    }
}

cout << len << endl;  // len 就是最终结果