Dijkstra算法的Java实现

 package main.java;

 import main.java.utils.GraphUtil;

 import java.util.ArrayDeque;
 import java.util.List;
 import java.util.Queue;

 /**
  * @Tme 2019/9/12 10:40
  * @Author chenhaisheng
  * @Email:ecjutsbs@foxmail.com
  */
 public class DijkstraTest {

     //邻接矩阵的表示
     public final static double[][] GRAPH_DISTANCE = GraphUtil.getDijkstraGraph();

     //起点到某节点的临时最短距离
     public static double distance[] = new double[GRAPH_DISTANCE.length];

     //某节点的前驱节点
     public static int pre[] = new int[GRAPH_DISTANCE.length];

     static int originIndex = 0, toIndex = 4;

     public static void main(String[] args) {

         init();
         findDijkstraShortestPath();
     }

     /*
     **初始化distance[]   pre[]
      */
     public static void init() {

         for (int i = 0; i < distance.length; i++) {
             if (i == originIndex) {
                 distance[i] = 0.0;
                 continue;
             }
             distance[i] = Double.MAX_VALUE;
         }

         for (int i = 0; i < pre.length; i++) {
             pre[i] = -1;
         }
     }

     public static void findDijkstraShortestPath() {

         //queue用于保存尚待搜索的节点
         Queue<Integer> queue = new ArrayDeque<>();

         //起始，将起始节点添加到queue
         queue.add(originIndex);

         while (queue.size() != 0) {

             Integer currentIndex = queue.poll();

             //获取当前节点的out-edges
             List<Integer> neighbours = getNeighbours(currentIndex);

             for (int i = 0; i < neighbours.size(); i++) {

                 //获取邻居节点的索引值
                 int neighbourIndex = neighbours.get(i);

                 //若起点经当前节点到邻居节点的距离 比直接到邻居节点的距离还小
                 if (distance[currentIndex] + getDistance(currentIndex, neighbourIndex) < distance[neighbourIndex]) {

                     //更新起点到邻居节点的距离
                     distance[neighbourIndex] = distance[currentIndex] + getDistance(currentIndex, neighbourIndex);

                     //设置下一个节点的前驱节点为当前节点
                     pre[neighbourIndex] = currentIndex;

                     //由于distance[neighbourIndex]已经改变，因此需要重新搜索neighbourIndex
                     queue.add(neighbourIndex);
                 }
             }
         }

         //输出从originIndex到toIndex的路径
         printPath(pre, originIndex, toIndex);
     }

     public static void printPath(int pre[], int from, int to) {

         //栈
         Deque<Integer> path = new ArrayDeque<>();

         path.push(to);

         int preIndex = pre[to];
         while (preIndex != from) {
             path.push(preIndex);
             preIndex = pre[preIndex];
         }

         path.push(from);

         while (!path.isEmpty()) {
             System.out.print(path.poll() + (path.size() > 0 ? "------>" : " "));
         }
         System.out.println(" ");
     }

     //获取当前节点所有的out-edges
     public static List getNeighbours(int index) {

         List<Integer> res = new ArrayList();

         //距离不为Double.MAX_VALUE,代表与当前节点连通
         for (int i = 0; i < GRAPH_DISTANCE[index].length; i++) {
             if (GRAPH_DISTANCE[index][i] != Double.MAX_VALUE)
                 res.add(i);
         }
         return res;
     }

     public static double getDistance(int from, int to) {
         return GRAPH_DISTANCE[from][to];
     }
 }

 package main.java.utils;

 /**
  * @Tme ${DATA} 19:10
  * @Author chenhaisheng
  * @Email:ecjutsbs@foxmail.com
  */
 public class GraphUtil<T> {

     public static double[][] getDijkstraGraph(){
         double max=Double.MAX_VALUE;
         double[][] graph={
                 {max,5,max,7,15},
                 {max,max,5,max,max},
                 {max,max,max,max,1},
                 {max,max,2,max,max},
                 {max,max,max,max,max}
         };
         return  graph;
     }
 }

对应的图：

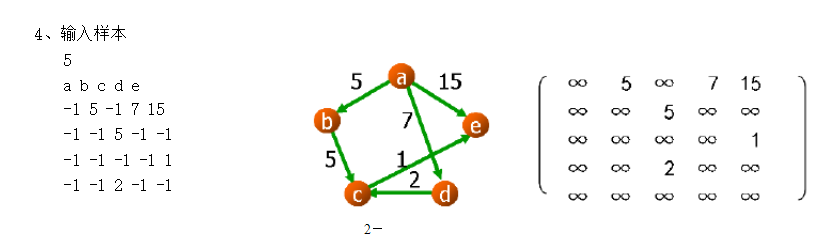
图的结构Ref：https://wenku.baidu.com/view/9fdeaa3c2b160b4e767fcff7.html

小结：

最重要的是记住：在搜索过程中，若节点i对应的distance[i]发生改变，那么对其任意一个邻居节点j，对应的distance[j]都要重新计算，继而引发连锁反应。

对某一个节点k，distance[k]通常会发生会多次改变。