ubuntu环境下测试cache大小并校验

Cache存储器：电脑中为高速缓冲存储器，是位于CPU和主存储器DRAM（Dynamic Random Access Memory）之间，规模较小，但速度很高的存储器，通常由SRAM（Static Random Access Memory 静态存储器）组成。它是位于CPU与内存间的一种容量较小但速度很高的存储器。CPU的速度远高于内存，当CPU直接从内存中存取数据时要等待一定时间周期，而Cache则可以保存CPU刚用过或循环使用的一部分数据，如果CPU需要再次使用该部分数据时可从Cache中直接调用，这样就避免了重复存取数据，减少了CPU的等待时间，因而提高了系统的效率。Cache又分为L1Cache（一级缓存）和L2Cache（二级缓存），L1Cache主要是集成在CPU内部，而L2Cache集成在主板上或是CPU上。

C++测试cache大小

代码

/*
* 代码思路：创建一个连续内存块，进行连贯、大量、随机的有意义访问，要保证整块内存尽可能全部放入cache。当
* 内存被整块放入cache中时，访问速度会明显加快，直到有一个时间跳跃点，消耗时间增多，则这个跳跃点的存储容* 量大小即为cache大小
*/

#include <iostream>
#include <random>
#include <ctime>
#include <algorithm>

#define KB(x) ((size_t)(x) << 10)

using namespace std;

int main()
{
    // 需要测试的数组的大小
    vector<size_t> sizes_KB;
    for (int i = 1; i < 18; i++)
    {
        sizes_KB.push_back(1 << i);
    }
    random_device rd;
    // 伪随机数算法，计算更快，占用内存更少
    mt19937 gen(rd());

    for (size_t size : sizes_KB)
    {
        // 离散均匀分布类
        uniform_int_distribution<> dis(0, KB(size) - 1);
        // 创建连续内存块
        vector<char> memory(KB(size));
        // 在内存中填入内容
        fill(memory.begin(), memory.end(), 1);

        int dummy = 0;

        // 在内存上进行大量的随机访问并计时
        clock_t begin = clock();
        // 1<<25：将1左移25位，进行大量随机访问
        for (int i = 0; i < (1 << 25); i++)
        {
            dummy += memory[dis(gen)];
        }
        clock_t end = clock();

        // 输出
        double elapsed_secs = double(end - begin) / CLOCKS_PER_SEC;
        cout << size << " KB, " << elapsed_secs << "secs, dummy:" << dummy << endl;
    }
}

运行结果

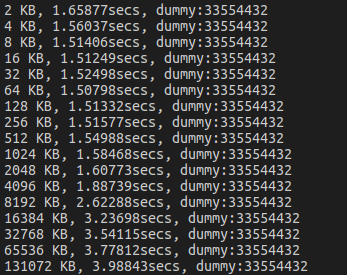
解析

由运行结果可以看出，内存访问时间在 8192KB 的时候发生了跳跃，由此推测cache的大小在 8192KB 左右，即8M左右，下面会进行验证。

ubuntu查看cahce大小

在命令行中输入如下代码：

getconf -a | grep CACHE

在本机环境中得到如下测试结果：

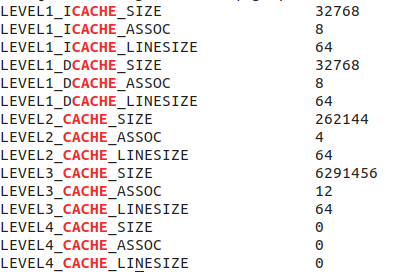
6291456/1024/1024 = 6M，所以本机chche大小为6M，与代码测试结果大体相符