伸展树(Splay tree)的基本操作与应用

伸展树的基本操作与应用

【伸展树的基本操作】

　　伸展树是二叉查找树的一种改进，与二叉查找树一样，伸展树也具有有序性。即伸展树中的每一个节点 x 都满足：该节点左子树中的每一个元素都小于 x，而其右子树中的每一个元素都大于 x。与普通二叉查找树不同的是，伸展树可以自我调整，这就要依靠伸展操作 Splay(x,S)。

伸展操作 Splay(x,S)　

　　伸展操作 Splay(x,S)是在保持伸展树有序性的前提下，通过一系列旋转将伸展树 S 中的元素 x 调整至树的根部。在调整的过程中，要分以下三种情况分别处理：

　　情况一：节点 x 的父节点 y 是根节点。这时，如果 x 是 y 的左孩子，我们进行一次 Zig（右旋）操作；如果 x 是 y 的右孩子，则我们进行一次 Zag（左旋）

操作。经过旋转，x 成为二叉查找树 S 的根节点，调整结束。如图 1 所示：

　　情况二：节点 x 的父节点 y 不是根节点，y 的父节点为 z，且 x 与 y 同时是各自父节点的左孩子或者同时是各自父节点的右孩子。这时，我们进行一次Zig-Zig 操作或者 Zag-Zag 操作。如图 2 所示：

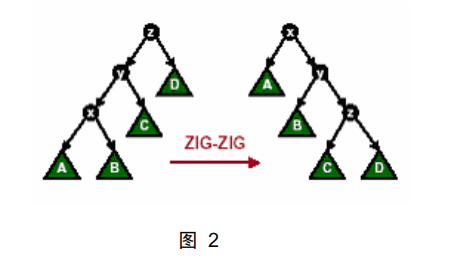
　　情况三：节点 x 的父节点 y 不是根节点，y 的父节点为 z，x 与 y 中一个是其父节点的左孩子而另一个是其父节点的右孩子。这时，我们进行一次 Zig-Zag 操作或者 Zag-Zig 操作。如图 3 所示：

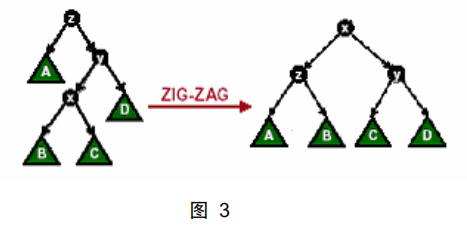
　　如图 4 所示，执行 Splay(1,S)，我们将元素 1 调整到了伸展树 S 的根部。再执行 Splay(2,S)，如图 5 所示，我们从直观上可以看出在经过调整后，伸展树比原来“平衡”了许多。而伸展操作的过程并不复杂，只需要根据情况进行旋转就可以了，而三种旋转都是由基本得左旋和右旋组成的，实现较为简单。

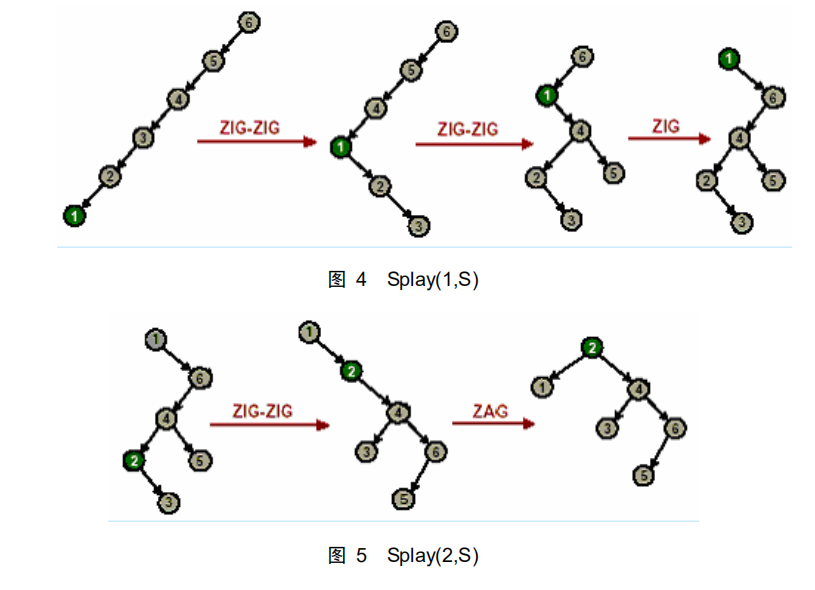
伸展树的基本操作

　　利用 Splay 操作，我们可以在伸展树 S 上进行如下运算：
　　(1)Find(x,S)：判断元素 x 是否在伸展树 S 表示的有序集中。
　　首先，与在二叉查找树中的查找操作一样，在伸展树中查找元素 x。如果 x
在树中，则再执行 Splay(x,S)调整伸展树。
　　(2)Insert(x,S)：将元素 x 插入伸展树 S 表示的有序集中。
　　首先，也与处理普通的二叉查找树一样，将 x 插入到伸展树 S 中的相应位置
上，再执行 Splay(x,S)。
　　(3)Delete(x,S)：将元素 x 从伸展树 S 所表示的有序集中删除。
　　首先，用在二叉查找树中查找元素的方法找到 x 的位置。如果 x 没有孩子或
只有一个孩子，那么直接将 x 删去，并通过 Splay 操作，将 x 节点的父节点调整
到伸展树的根节点处。否则，则向下查找 x 的后继 y，用 y 替代 x 的位置，最后
执行 Splay(y,S)，将 y 调整为伸展树的根。
　　(4)Join(S1,S2)：将两个伸展树 S1 与 S2 合并成为一个伸展树。其中 S1 的所
有元素都小于 S2 的所有元素。
　　首先，我们找到伸展树 S1 中最大的一个元素 x，再通过 Splay(x,S1)将 x 调
整到伸展树 S1 的根。然后再将 S2 作为 x 节点的右子树。这样，就得到了新的
伸展树 S。如图 6 所示

　　

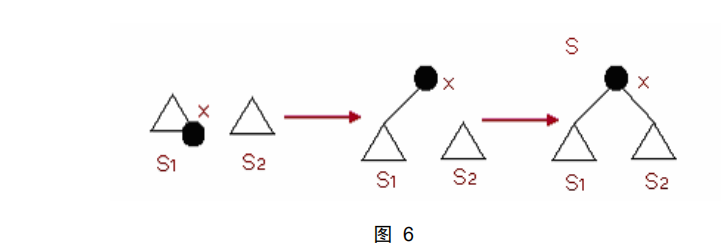
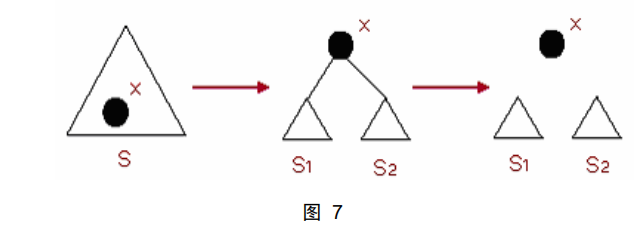
　　(5)Split(x,S)：以 x 为界，将伸展树 S 分离为两棵伸展树 S1 和 S2，其中 S1
中所有元素都小于 x，S2 中的所有元素都大于 x。
　　首先执行 Find(x,S)，将元素 x 调整为伸展树的根节点，则 x 的左子树就是
S1，而右子树为 S2。如图 7 所示

　　除了上面介绍的五种基本操作，伸展树还支持求最大值、求最小值、求前趋，

求后继等多种操作，这些基本操作也都是建立在伸展操作的基础上的。

时间复杂度分析

　　由以上这些操作的实现过程可以看出，它们的时间效率完全取决于 Splay 操
作的时间复杂度。下面，我们就用会计方法来分析 Splay 操作的平摊复杂度。
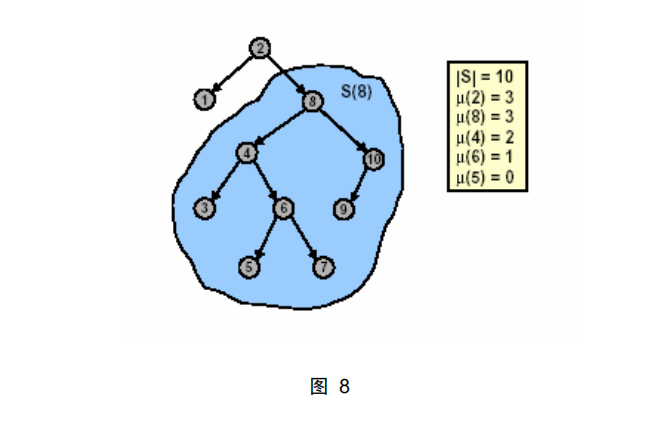
　　首先，我们定义一些符号：S(x)表示以节点 x 为根的子树。|S|表示伸展树 S
的节点个数。令μ(S) = [ log|S| ]，μ(x)=μ(S(x))。如图 8 所示

　　我们用 1 元钱表示单位代价（这里我们将对于某个点访问和旋转看作一个单位时间的代价）。定义伸展树不变量：在任意时刻，伸展树中的任意节点 x 都至少有μ(x)元的存款。

　　 在 Splay 调整过程中，费用将会用在以下两个方面：

　　　　 (1)为使用的时间付费。也就是每一次单位时间的操作，我们要支付 1 元钱。

　　　　 (2)当伸展树的形状调整时，我们需要加入一些钱或者重新分配原来树中每个节点的存款，以保持不变量继续成立。

　　下面我们给出关于 Splay 操作花费的定理：

　　　　定理：在每一次 Splay(x,S)操作中，调整树的结构与保持伸展树不变量的总花费不超过 3μ(S)+1。

　　　　 证明：用μ(x)和μ’(x)分别表示在进行一次 Zig、Zig-Zig 或 Zig-Zag 操作前后节点 x 处的存款。

　　 　　下面我们分三种情况分析旋转操作的花费：

　　　　情况一：如图 9 所示

　　

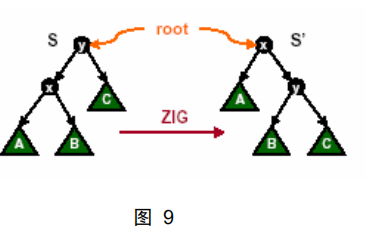
　　　　我们进行 Zig 或者 Zag 操作时，为了保持伸展树不变量继续成立，我们需要
　　花费：
　　　　　　　　μ’(x) +μ’(y) -μ(x) -μ(y) = μ’(y) -μ(x)
　　　　　　　　　　　　　　　　　　≤ μ’(x) -μ(x)
　　　　　　　　　　　　　　　　　　≤ 3(μ’(x) -μ(x))
　　　　　　　　　　　　　　　　　　= 3(μ(S) -μ(x))
　　　　此外我们花费另外 1 元钱用来支付访问、旋转的基本操作。因此，一次 Zig
　　或 Zag 操作的花费至多为 3(μ(S) -μ(x))。
　　情况二：如图 10 所示

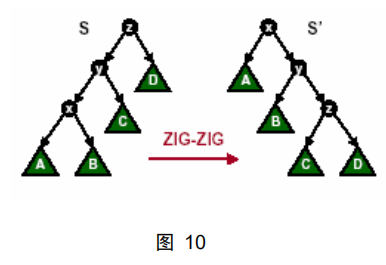
　　我们进行 Zig-Zig 操作时，为了保持伸展树不变量，我们需要花费：

　　　　 μ’(x) +μ’(y) +μ’(z) -μ(x) -μ(y) -μ(z) = μ’(y) +μ’(z) -μ(x) -μ(y) = (μ’(y) -μ(x)) + (μ’(z) -μ(y))

​ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　≤ (μ’(x) -μ(x)) + (μ’(x) -μ(x))

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　= 2 (μ’(x) -μ(x))

　　​ 与上种情况一样，我们也需要花费另外的 1 元钱来支付单位时间的操作。 当μ’(x) <μ(x) 时，显然 2 (μ’(x) -μ(x)) +1 ≤ 3 (μ’(x) -μ(x))。也就是进行Zig-Zig 操作的花费不超过 3 (μ’(x) -μ(x))。 当μ’(x) =μ(x) 时，我们可以证明μ’(x) +μ’(y) + μ’(z) <μ(x) +μ(y) +μ(z)，也就是说我们不需要任何花费保持伸展树不变量，并且可以得到退回来的钱，用其中的 1 元支付访问、旋转等操作的费用。为了证明这一点，我们假设μ’(x) +μ’(y)+μ’(z) >μ(x) +μ(y) +μ(z)。 联系图 9，我们有μ(x) =μ’(x) =μ(z)。那么，显然μ(x) =μ(y) =μ(z)。于是，可以得出μ(x) =μ’(z) =μ(z)。

　　令 a = 1 + |A| + |B|，b = 1 + |C| + |D|，那么就有 [log a] = [log b] = [log (a+b+1)]。 ①

　　我们不妨设 b≥a，则有 [log (a+b+1)] ≥ [log (2a)] = 1+[log a]> [log a]                      ②

　　①与②矛盾，所以我们可以得到μ’(x) =μ(x) 时，Zig-Zig 操作不需要任何花
费，显然也不超过 3 (μ’(x) -μ(x))。
　　情况三：与情况二类似，我们可以证明，每次 Zig-Zag 操作的花费也不超过
3 (μ’(x) -μ(x))。
　　以上三种情况说明，Zig 操作花费最多为 3(μ(S)-μ(x))+1，Zig-Zig 或 Zig-Zag
操作最多花费 3(μ’(x)-μ(x))。那么将旋转操作的花费依次累加，则一次 Splay(x,S)
操作的费用就不会超过 3μ(S)+1。也就是说对于伸展树的各种以 Splay 操作为基
础的基本操作的平摊复杂度，都是 O(log n)。所以说，伸展树是一种时间效率非
常优秀的数据结构.

【伸展树的应用】

　　伸展树作为一种时间效率很高、空间要求不大的数据结构，在解题中有很大
的用武之地。下面就通过一个例子说明伸展树在解题中的应用。
例：营业额统计 Turnover (湖南省队 2002 年选拔赛)
题目大意
　　Tiger 最近被公司升任为营业部经理，他上任后接受公司交给的第一项任务
便是统计并分析公司成立以来的营业情况。Tiger 拿出了公司的账本，账本上记
录了公司成立以来每天的营业额。分析营业情况是一项相当复杂的工作。由于节
假日，大减价或者是其他情况的时候，营业额会出现一定的波动，当然一定的波
动是能够接受的，但是在某些时候营业额突变得很高或是很低，这就证明公司此
时的经营状况出现了问题。经济管理学上定义了一种最小波动值来衡量这种情
况：
　　该天的最小波动值= min { | 该天以前某一天的营业额-该天的营业额 | }
　　当最小波动值越大时，就说明营业情况越不稳定。而分析整个公司的从成立
到现在营业情况是否稳定，只需要把每一天的最小波动值加起来就可以了。你的
任务就是编写一个程序帮助 Tiger 来计算这一个值。
　　注：第一天的最小波动值为第一天的营业额。
　　数据范围：天数 n≤32767，每天的营业额 ai≤1,000,000。最后结果 T≤2
31。

初步分析
　　题目的意思非常明确，关键是要每次读入一个数，并且在前面输入的数中找
到一个与该数相差最小的一个。
　　我们很容易想到 O(n2)的算法：每次读入一个数，再将前面输入的数一次查
找一遍，求出与当前数的最小差值，记入总结果 T。但由于本题中 n 很大，这样
的算法是不可能在时限内出解的。而如果使用线段树记录已经读入的数，就需要
记下一个 2M 的大数组，这在当时比赛使用 TurboPascal 7.0 编程的情况下是不可
能实现的。而前文提到的红黑树与平衡二叉树虽然在时间效率、空间复杂度上都
比较优秀，但过高的编程复杂度却让人望而却步。于是我们想到了伸展树算法。

算法描述
　　进一步分析本题，解题中，涉及到对于有序集的三种操作：插入、求前趋、
求后继。而对于这三种操作，伸展树的时间复杂度都非常优秀，于是我们设计了
如下算法：
　　开始时，树 S 为空，总和 T 为零。每次读入一个数 p，执行 Insert(p,S)，将 p
插入伸展树 S。这时，p 也被调整到伸展树的根节点。这时，求出 p 点左子树中
的最右点和右子树中的最左点，这两个点分别是有序集中 p 的前趋和后继。然后
求得最小差值，加入最后结果 T。
解题小结
　　由于对于伸展树的基本操作的平摊复杂度都是 O(log n)的，所以整个算法的
时间复杂度是 O(nlog n)，可以在时限内出解。而空间上，可以用数组模拟指针
存储树状结构，这样所用内存不超过 400K，在 TP 中使用动态内存就可以了。
编程复杂度方面，伸展树算法非常简单，程序并不复杂。虽然伸展树算法并不是
本题唯一的算法，但它与其他常用的数据结构相比还是有很多优势的。下面的表
格就反映了在解决这一题时各个算法的复杂度。从中可以看出伸展树在各方面都
是优秀的，这样的算法很适合在竞赛中使用。

【总结】

由上面的分析介绍，我们可以发现伸展树有以下几个优点： (1)时间复杂度低，伸展树的各种基本操作的平摊复杂度都是 O(log n)的。在树状数据结构中，无疑是非常优秀的。

(2)空间要求不高。与红黑树需要记录每个节点的颜色、AVL 树需要记录平衡因子不同，伸展树不需要记录任何信息以保持树的平衡。 (3)算法简单，编程容易。伸展树的基本操作都是以 Splay 操作为基础的，而Splay 操作中只需根据当前节点的位置进行旋转操作即可。

上题参考代码：

 /**************************************************************
     Problem: 1588
     User: SongHL
     Language: C++
     Result: Accepted
     Time:1284 ms
     Memory:2068 kb
 ****************************************************************/
 
 #include<bits/stdc++.h>
 const int INF=0x3f3f3f3f;
 using namespace std;
 int ans,n,t1,t2,rt,size;
 int tr[][],fa[],num[];
 void rotate(int x,int &k)
 {
     int y=fa[x],z=fa[y],l,r;
     if(tr[y][]==x)l=;else l=;r=l^;
     if(y==k)k=x;
     else{if(tr[z][]==y)tr[z][]=x;else tr[z][]=x;}
     fa[x]=z;fa[y]=x;fa[tr[x][r]]=y;
     tr[y][l]=tr[x][r];tr[x][r]=y;
  }
 void splay(int x,int &k)
 {
     int y,z;
     while(x!=k)
     {
         y=fa[x],z=fa[y];
         if(y!=k)
         {
             if((tr[y][]==x)^(tr[z][]==y))rotate(x,k);
             else rotate(y,k);
         }
         rotate(x,k);
     }
 }
 void ins(int &k,int x,int last)
 {
      if(k==){size++;k=size;num[k]=x;fa[k]=last;splay(k,rt);return;}
      if(x<num[k])ins(tr[k][],x,k);
      else ins(tr[k][],x,k);
  }
 void ask_before(int k,int x)
 {
      if(k==)return;
      if(num[k]<=x){t1=num[k];ask_before(tr[k][],x);}
      else ask_before(tr[k][],x);
  }
 void ask_after(int k,int x)
 {
    if(k==)return;
    if(num[k]>=x){t2=num[k];ask_after(tr[k][],x);}
    else ask_after(tr[k][],x);
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         int x;if(scanf("%d",&x)==EOF) x=;
         t1=-INF;t2=INF;
         ask_before(rt,x);
         ask_after(rt,x);
         if(i!=)ans+=min(x-t1,t2-x);
         else ans+=x;
         ins(rt,x,);
     }
     printf("%d",ans);
     return ;
 }

平衡树的基本操作实现代码

[NOI2005]维修数列

https://www.lydsy.com/JudgeOnline/problem.php?id=1500

算法过程：

初始化

首先，对于原序列，我们不应该一个一个读入，然后插入，那么效率就是O(nlogn),而splay的常数本身就很大，所以考虑一个优化，就是把原序列一次性读入后，直接类似线段树的build，搞一个整体建树，即不断的将当前点维护的区间进行二分，到达单元素区间后，就把对应的序列值插入进去，这样，我们一开始建的树就是一个非常平衡的树，可以使后续操作的常数更小，并且建树整个复杂度只是O(2n)的。

Insert操作

其次，我们来考虑一下如何维护一个insert操作。我们可以这么做，首先如上将需要insert的区间变成节点数目为tot的平衡树,然后把k+1（注意我们将需要操作的区间右移了一个单位，所以题目所给k就是我们需要操作的k+1）移到根节点的位置，把原树中的k+2移到根节点的右儿子的位置。然后把需要insert的区间，先build成一个平衡树，把需要insert的树的根直接挂到原树中k+1的左儿子上就行了。

Delete操作

再然后，我们来考虑一下delete操作，我们同样的，把需要delete的区间变成[k+1,k+tot]（注意，是删去k后面的tot个数，那么可以发现我们需要操作的原区间是[k,k+tot-1]!），然后把k号节点移到根节点的位置，把k+tot+2移到根节点的右儿子位置，然后直接把k+tot+2的左儿子的指针清为0，就把这段区间删掉了。可以发现，比insert还简单一点。

Reverse操作

接下来，这道题的重头戏就要开始了。splay的区间操作基本原理还类似于线段树的区间操作，即延迟修改，又称打懒标记。

对于翻转（reverse）操作，我们依旧是将操作区间变成[k+1,k+tot]，然后把k和k+tot+1分别移到对应根的右儿子的位置，然后对这个右儿子的左儿子打上翻转标记即可。

Make-Same操作

对于Make-Same操作，我们同样需要先将需要操作的区间变成[k+1,k+tot]，然后把k和k+tot+1分别移到根和右儿子的位置，然后对这个右儿子的左儿子打上修改标记即可。

Get-Sum操作

对于Get-Sum操作，我们还是将操作区间变成[k+1,k+tot],然后把k和k+tot+1分别移到根和右儿子的位置，然后直接输出这个右儿子的左儿子上的sum记录的和。

Max-Sum操作

对于这个求最大子序列的操作，即Max-Sum操作，我们不能局限于最开始学最大子序列的线性dp方法，而是要注意刚开始，基本很多书都会介绍一个分治的O(nlogn)的方法，但是由于存在O(n)的方法，导致这个方法并不受重视，但是这个方法确实很巧妙，当数列存在修改操作时，线性的算法就不再适用了。

这种带修改的最大子序列的问题，最开始是由线段树来维护，具体来说就是，对于线段树上的每个节点所代表的区间，维护3个量：lx表示从区间左端点l开始的连续的前缀最大子序列。rx表示从区间右端点r开始的连续的后缀最大子序列。mx表示这个区间中的最大子序列。

那么在合并[l,mid]和[mid+1,r]时，就类似一个dp的过程了！其中

lx[l,r]=max(lx[l,mid],sum[l,mid]+lx[mid+1,r])lx[l,r]=max(lx[l,mid],sum[l,mid]+lx[mid+1,r])

rx[l,r]=max(rx[mid+1,r],sum[mid+1,r]+rx[l,mid])rx[l,r]=max(rx[mid+1,r],sum[mid+1,r]+rx[l,mid])

mx[l,r]=max(mx[l,mid],mx[mid+1,r],lx[mid+1,r]+rx[l,mid+1])mx[l,r]=max(mx[l,mid],mx[mid+1,r],lx[mid+1,r]+rx[l,mid+1])

这个还是很好理解的。就是选不选mid的两个决策。但是其实在实现的时候，我们并不用[l,r]的二维方式来记录这三个标记，而是用对应的节点编号来表示区间，这个可以看程序，其实是个很简单的东西。

那么最大子序列这个询问操作就可以很简单的解决了，还是类比前面的方法，就是把k和k+tot+1移到对应的根和右儿子的位置，然后直接输出右儿子的左儿子上的mx标记即可

懒标记的处理

最后，相信认真看了的童鞋会有疑问，这个标记怎么下传呢？首先，我们在每次将k和k+tot+1移到对应的位置时，需要一个类似查找k大值的find操作，即找出在平衡树中，实际编号为k在树中中序遍历的编号，这个才是我们真正需要处理的区间端点编号，那么就好了，我们只需在查找的过程中下传标记就好了！（其实线段树中也是这么做的），因为我们所有的操作都需要先find一下，所以我们可以保证才每次操作的结果计算出来时，对应的节点的标记都已经传好了。而我们在修改时，直接修改对应节点的记录标记和懒标记，因为我们的懒标记记录的都是已经对当前节点产生贡献，但是还没有当前节点的子树区间产生贡献！然后就是每处有修改的地方都要pushup一下就好了。

一些细节

另外，由于本题数据空间卡的非常紧，我们就需要用时间换空间，直接开4000000*logm的数据是不现实的，但是由于题目保证了同一时间在序列中的数字的个数最多是500000，所以我们考虑一个回收机制，把用过但是已经删掉的节点编号记录到一个队列或栈中，在新建节点时直接把队列中的冗余编号搞过来就好了。

参考代码：

 #include<bits/stdc++.h>
 #define RI register int
 #define For(i,a,b) for (RI i=a;i<=b;++i)
 using namespace std;
 const int inf=0x3f3f3f3f;
 const int N=1e6+;
 int n,m,rt,cnt;
 int a[N],id[N],fa[N],c[N][];
 int sum[N],sz[N],v[N],mx[N],lx[N],rx[N];
 bool tag[N],rev[N];
 //tag表示是否有统一修改的标记，rev表示是否有统一翻转的标记
 //sum表示这个点的子树中的权值和，v表示这个点的权值
 queue<int> q;
 inline int read()
 {
     RI x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-') f=-; ch=getchar();}
     while(''<=ch&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }
 inline void pushup(RI x)
 {
     RI l=c[x][],r=c[x][];
     sum[x]=sum[l]+sum[r]+v[x];
     sz[x]=sz[l]+sz[r]+;
     mx[x]=max(mx[l],max(mx[r],rx[l]+v[x]+lx[r]));
     lx[x]=max(lx[l],sum[l]+v[x]+lx[r]);
     rx[x]=max(rx[r],sum[r]+v[x]+rx[l]);
 }
 //上传记录标记
 inline void pushdown(RI x)
 {
     RI l=c[x][],r=c[x][];
     if(tag[x])
     {
         rev[x]=tag[x]=;//我们有了一个统一修改的标记，再翻转就没有什么意义了
         if(l) tag[l]=,v[l]=v[x],sum[l]=v[x]*sz[l];
         if(r) tag[r]=,v[r]=v[x],sum[r]=v[x]*sz[r];
         if(v[x]>=)
         {
             if(l) lx[l]=rx[l]=mx[l]=sum[l];
             if(r) lx[r]=rx[r]=mx[r]=sum[r];
         }
         else
         {
             if(l) lx[l]=rx[l]=,mx[l]=v[x];
             if(r) lx[r]=rx[r]=,mx[r]=v[x];
         }
     }
     if(rev[x])
     {
         rev[x]=;rev[l]^=;rev[r]^=;
         swap(lx[l],rx[l]);swap(lx[r],rx[r]);
         //注意，在翻转操作中，前后缀的最长上升子序列都反过来了，很容易错
         swap(c[l][],c[l][]);swap(c[r][],c[r][]);
     }
 }
 inline void rotate(RI x,RI &k)
 {
     RI y=fa[x],z=fa[y],l=(c[y][]==x),r=l^;
     if (y==k)k=x;else c[z][c[z][]==y]=x;
     fa[c[x][r]]=y;fa[y]=x;fa[x]=z;
     c[y][l]=c[x][r];c[x][r]=y;
     pushup(y);pushup(x);
     //旋转操作,一定要上传标记且顺序不能变
 }
 inline void splay(RI x,RI &k)
 {
     while(x!=k)
     {
         int y=fa[x],z=fa[y];
         if(y!=k)
         {
             if((c[z][]==y)^(c[y][]==x)) rotate(x,k);
             else rotate(y,k);
         }
         rotate(x,k);
     }
 }
 //这是整个程序的核心之一，毕竟是伸展操作嘛
 inline int find(RI x,RI rk)
 {//返回当前序列第rk个数的标号
     pushdown(x);
     RI l=c[x][],r=c[x][];
     if(sz[l]+==rk) return x;
     if(sz[l]>=rk) return find(l,rk);
     else return find(r,rk-sz[l]-);
 }
 inline void recycle(RI x)
 {//这就是用时间换空间的回收冗余编号机制，很好理解
     RI &l=c[x][],&r=c[x][];
     if(l) recycle(l);
     if(r) recycle(r);
     q.push(x);
     fa[x]=l=r=tag[x]=rev[x]=;
 }
 inline int split(RI k,RI tot)//找到[k+1,k+tot]
 {
     RI x=find(rt,k),y=find(rt,k+tot+);
     splay(x,rt);splay(y,c[x][]);
     return c[y][];
 }
 //这个split操作是整个程序的核心之三
 //我们通过这个split操作，找到[k+1,k+tot]，并把k,和k+tot+1移到根和右儿子的位置
 //然后我们返回了这个右儿子的左儿子，这就是我们需要操作的区间
 inline void query(RI k,RI tot)
 {
     RI x=split(k,tot);
     printf("%d\n",sum[x]);
 }
 inline void modify(RI k,RI tot,RI val)//MAKE-SAME
 {
     RI x=split(k,tot),y=fa[x];
     v[x]=val;tag[x]=;sum[x]=sz[x]*val;
     if(val>=) lx[x]=rx[x]=mx[x]=sum[x];
         else lx[x]=rx[x]=,mx[x]=val;
     pushup(y);pushup(fa[y]);
     //每一步的修改操作，由于父子关系发生改变
     //及记录标记发生改变，我们需要及时上传记录标记
 }
 inline void rever(RI k,RI tot)//翻转
 {
     RI x=split(k,tot),y=fa[x];
     if(!tag[x])
     {
         rev[x]^=;
         swap(c[x][],c[x][]);
         swap(lx[x],rx[x]);
         pushup(y);pushup(fa[y]);
     }
     //同上
 }
 inline void erase(RI k,RI tot)//DELETE
 {
     RI x=split(k,tot),y=fa[x];
     recycle(x);c[y][]=;
     pushup(y);pushup(fa[y]);
     //同上
 }
 inline void build(RI l,RI r,RI f)
 {
     RI mid=(l+r)>>,now=id[mid],pre=id[f];
     if(l==r)
     {
         mx[now]=sum[now]=a[l];
         tag[now]=rev[now]=;
         //这里这个tag和rev的清0是必要，因为这个编号可能是之前冗余了
         lx[now]=rx[now]=max(a[l],);
         sz[now]=;
     }
     if(l<mid) build(l,mid-,mid);
     if(mid<r) build(mid+,r,mid);
     v[now]=a[mid]; fa[now]=pre;
     pushup(now); //上传记录标记
     c[pre][mid>=f]=now;
     //当mid>=f时，now是插入到又区间取了，所以c[pre][1]=now，当mid<f时同理
 }
 inline void insert(RI k,RI tot)
 {
     for(int i=;i<=tot;++i) a[i]=read();
     for(int i=;i<=tot;++i)
     {
         if(!q.empty()) id[i]=q.front(),q.pop();
         else id[i]=++cnt;//利用队列中记录的冗余节点编号
     }
     build(,tot,);
     RI z=id[(+tot)>>];
     RI x=find(rt,k+),y=find(rt,k+);
      //首先，依据中序遍历，找到我们需要操作的区间的实际编号
     splay(x,rt);splay(y,c[x][]);
     //把k+1(注意我们已经右移了一个单位）和(k+1)+1移到根和右儿子
     fa[z]=y;c[y][]=z;
     //直接把需要插入的这个平衡树挂到右儿子的左儿子上去就好了
     pushup(y);pushup(x);
     //上传记录标记
 }
 //可以这么记，只要用了split就要重新上传标记
 //只有find中需要下传标记
 int main()
 {
     n=read(),m=read();
     mx[]=a[]=a[n+]=-inf;
     For(i,,n) a[i+]=read();
     For(i,,n+) id[i]=i;//虚拟了两个节点1和n+2，然后把需要操作区间整体右移一个单位
     build(,n+,);//建树
     rt=(n+)>>;cnt=n+;//取最中间的为根
     RI k,tot,val;char ch[];
     while(m--)
     {
         scanf("%s",ch);
         if(ch[]!='M' || ch[]!='X') k=read(),tot=read();
         if(ch[]=='I') insert(k,tot);
         if(ch[]=='D') erase(k,tot);//DELETE
         if(ch[]=='M')
         {
             if(ch[]=='X') printf("%d\n",mx[rt]);//MAX-SUM
             else val=read(),modify(k,tot,val);//MAKE-SAME
         }
         if(ch[]=='R') rever(k,tot);//翻转
         if(ch[]=='G') query(k,tot);//GET-SUM
     }
     return ;
 }