【3】Decision tree（决策树）

前言

---

Decision tree is one of the most popular classification tools

它用一个训练数据集学到一个映射，该映射以未知类别的新实例作为输入，输出对这个实例类别的预测。

决策树相当于将一系列问题组织成树，具体说，每个问题对应一个属性，根据属性值来生成判断分支，一直到决策树的叶节点就产生了类别。

那么，接下来的问题就是怎么选择最佳的属性作为当前的判断分支，这就引出了用信息论划分数据集的方式。

在信息论中，划分数据之前和之后信息发生的信息变化成为信息增益。

本文主要介绍的决策树算法是ID3，它的核心是将获得信息增益最高的特征作为最好的选择。

他和C4.5算法不同的是C4.5算法使用的是信息增益比最高的特征作为最好的选择。

本文参考书是《机器学习实战》

信息增益

---

信息论中每个符号x的信息量成为自信息，定义为：

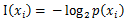
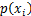其中是选择该分类的概率。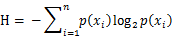

熵（entropy）定义为信息的期望值，意思是每个符号的平均信息量，其公式为：

给定一个数据集，最后一列默认为类别标签的时候，根据数据集计算数据集的香农熵的代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14

#基于最后一列的分类标签，计算给定数据集的香农熵 def calcShannonEnt(dataset):     num_of_entries = len(dataset)     label_counts = {}     for feat_vec in dataset:         current_lebel = feat_vec[-1]         if current_lebel not in label_counts.keys():             label_counts[current_lebel] = 0         label_counts[current_lebel] += 1     shannonEnt = 0.0     for value in label_counts.values():         prob = float(value)/num_of_entries         shannonEnt -= prob*log(prob, 2)     return shannonEnt

要得到信息增益，我们还需要对每个特征划分数据集的结果计算一次信息熵。

所以首先如要划分数据集。按照给定特征的某个值把属于这个值的数据集部分划分出来，代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

# ================================= # 按照给定特征划分数据集 # 输入：dataset数据集； #       axis指定特征，用下标表示； #       value需要返回的特征的值 # 返回：数据集中特征值等于value的子集 # ================================= def splitDataset(dataset, axis, value):     retDataset = []     for featVec in dataset:         if featVec[axis] == value:             reducedFeatVec = featVec[0:axis]             reducedFeatVec.extend(featVec[axis+1:])             retDataset.append(reducedFeatVec)     return  retDataset

具体到这个算法来说，应该选择能使信息增益最大的特征作为数据集的划分方式。

信息增益等于原始数据集的熵减去某个特征所带来的信息熵。

计算某个特征的信息熵以及基于此选择最好的数据集划分方式的代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

# =============================================== # 输入： #        dataSet: 数据集 # 输出： #        bestFeature: 和原数据集熵差最大划分对应的特征的列号 # =============================================== def chooseBestFeatureToSplit(dataSet):     # 最后一列用于标签，剩下的才是特征     numFeatures = len(dataSet[0]) - 1     # 根据标签计算的熵     baseEntropy = calcShannonEnt(dataSet)     bestInfoGain = 0.0; bestFeature = -1     # iterate over all the features     for i in range(numFeatures):         # 取出某个特征列的所有值         featList = [example[i] for example in dataSet]         # 去重         uniqueVals = set(featList)         newEntropy = 0.0         for value in uniqueVals:             subDataSet = splitDataset(dataSet, i, value)             prob = len(subDataSet)/float(len(dataSet))             newEntropy += prob * calcShannonEnt(subDataSet)         # calculate the info gain，计算信息增益         infoGain = baseEntropy - newEntropy         # 和目前最佳信息增益比较，如果更大则替换掉         if (infoGain > bestInfoGain):             bestInfoGain = infoGain             bestFeature = i     # 返回代表某个特征的下标     return bestFeature

用一下代码去测试：

1 2 3 4 5 6 7 8 9 10 11 12 13 14

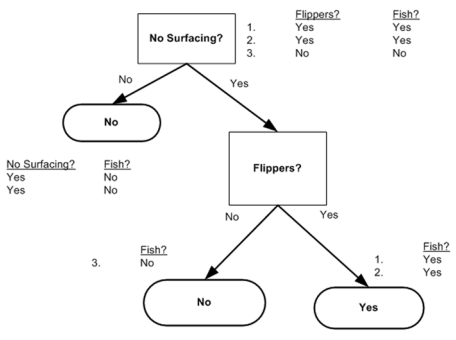
#用于生成数据集，测试计算熵的函数 def testDataset():     dataset1 = [[1, 1, 'yes'],                [1, 1, 'yes'],                [1, 0, 'no'],                [0, 1, 'no'],                [0, 1, 'no']]     labels = ['no surfacing', 'flippers']     return dataset1, labels   # 用于测试的函数 def test():     mydata, labels = testDataset()     print chooseBestFeatureToSplit(mydata)

可得到如下结果：

结果表明，第0个特征是用来划分数据集最好的。

递归构建决策树

---

选择了一个特征进行划分之后，数据将被传递到树分支的下一个节点，在这个节点上，我们可以再次划分数据。

所以这是一个递归的过程。

递归结束的条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有势力都属于同一个分类。

在Python中可以使用字典来表示一棵树，例如这样的一棵树

可以用字典{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}表示

但是这里还可能出现另一种可能，就是所有用来划分数据集的属性全部用完之后，类别标签依然不是唯一的

这种情况我们采用少数服从多数来解决。所以我们需要一个找出多数类别的函数，如下：

1 2 3 4 5 6 7 8 9 10 11 12

# 传入分类名称组成的列表，返回出现次数最多的分类名称 import operator def majorityCnt(class_list):     classCount = {}     for vote in class_list:         if vote not in classCount:             classCount[vote] = 0         classCount[vote] += 1     sorted_class_list = sorted(classCount.iteritems(),                                key = operator.itemgetter(1),                                reverse=True)     return sorted_class_list[0][0]

接下来是创建树的代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

# =============================================== # 本函数用于创建决策树 # 输入： #        dataSet: 数据集 #        labels: 划分特征标签集 # 输出： #        myTree: 生成的决策树 # =============================================== def createTree(dataSet, labels):     # 获得类别标签列表     classList = [example[-1] for example in dataSet]     # 递归终止条件一：如果数据集内所有分类一致     if classList.count(classList[0]) == len(classList):         return classList[0]     # 递归终止条件二：如果所有特征都划分完毕，任然不能将数据集划分成仅仅包含唯一类别的分组     if len(dataSet[0]) == 1:  # 只剩下一列为类别列         return majorityCnt(classList) # 返回出现次数最多的类别     # 选择最佳划分特征，返回的时候特征的下标     best_feature = chooseBestFeatureToSplit(dataSet)     best_feat_label = labels[best_feature]     # 创建空树     myTree = {best_feat_label:{}}     # 删除划分后的特征标签     del(labels[best_feature])     # 获取最佳划分特征中全部的特征值     featValues = [example[best_feature] for example in dataSet]     # 去重     uniqueVals = set(featValues)     for value in uniqueVals:         subLabels = labels[:]  # 保存用于下一次递归         myTree[best_feat_label][value] = createTree(splitDataset(dataSet, best_feature, value), subLabels)       return myTree

至此，决策树就算构造完成了。

测试一下效果：

序列化存储

---

由于决策树构造使用递归算法，如果数据集过大的话将会产生很大的开销。

所以构造好一个决策树我们可以把它保存起来，这样就不用每次使用都构造。

保存的方式使“序列化”，在Python中又叫“pickling”,它的反操作叫反序列化——“unpickling”。

任何对象都可以执行序列化操作。

本文中用于把树序列化的代码如下：

1 2 3 4 5 6 7 8 9 10 11 12

# 把传入的树序列化之后存入文件 def storeTree(inputTree, filename):     import pickle # 用于序列化的模块     fw = open(filename, 'w')     pickle.dump(inputTree, fw)     fw.close()   # 从文件中把存好的树反序列化出来 def grabTree(filename):     import pickle     fr = open(filename)     return pickle.load(filename)

来自为知笔记(Wiz)