Distilling the Knowledge in a Neural Network

url: https://arxiv.org/abs/1503.02531

year: NIPS 2014

简介

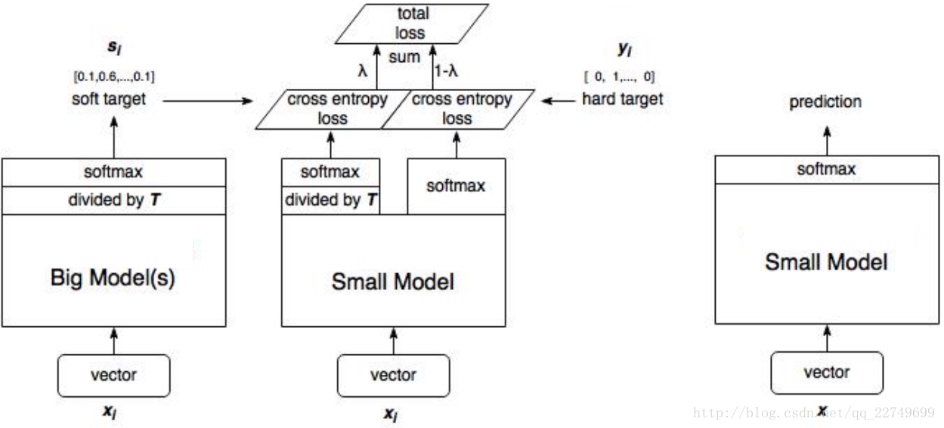
将大模型的泛化能力转移到小模型的一种显而易见的方法是使用由大模型产生的类概率作为训练小模型的“软目标”

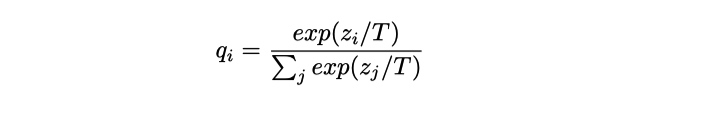
其中, T(temperature, 蒸馏温度), 通常设置为1的。使用较高的T值可以产生更软的类别概率分布。也就是, 较高的 T 值, 让学生的概率分布可以更加的接近与老师的概率分布,

下面通过一个直观的例子来感受下

def softmax_with_T(logits, temperature):

    for t in temperature:

        total = 0

        prob = []

        for logit in logits:

            total += np.exp(logit/t)

        for logit in logits:

            prob.append(np.exp(logit/t) / total)

        print('T={:<4d}'.format(t), end='  ')

        for p in prob:

            print('{:0.3f}'.format(p), end='  ')

        print()

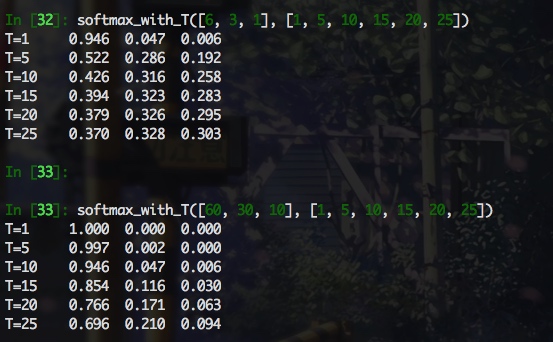
可以看出, softmax 输出的项比例与 logits原始比例之间的关系与 logits 本身的模长以及 T 值大小相关, 感觉 T 值需要仔细调整下, 至少能反应 logits 之间的大致关系, 而且可以看出, softmax_with_T 受两个变量的影响, 直接来比较的话, 比较难分析. 当 T 远大于 logits 的模长时, softmax 的输出尺度在相同的数量级下(如logits=[6,3,1], T=25), 这样看的话, 即使老师和学生的 logit 相差很远, 经过具有很大 T 的 softamx 之后, 数量级几乎相同, 这样是不合理的. 但是, 下面的公式推导结果加上实验结果表明, 认真看梯度才是王道, 看输出的话, 完全找不到感觉, 对于软标签交叉熵损失

梯度推导

softmax+cross entropy梯度求导

\[\bf{{\frac{\partial{C}}{\partial{z_i}} = \frac{1}{T}(q_i-p_i)
= \frac{1}{T} \left( \frac{e^{z_i/T}}{\sum_je^{z_j/T}} - \frac{e^{v_i/T}}{\sum_je^{v_j/T}}\right)}}
\]

\(e^x\)泰勒展开

\[\bf {e^x \approx 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!} \\
x\rightarrow 0, \quad e^x \approx 1+x}
\]

\(T\rightarrow \infty\)时, \(\frac{Z_i}{T}\rightarrow 0\)

\[\bf {{\frac{\partial{C}}{\partial{z_i}} \approx \frac{1}{T} \left(\frac{{1+{z_i/T}}}{N+\sum {z_j/T}} -\frac{{1+{v_i/T}}}{N+\sum {v_j/T}}\right)}}
\]

假设logits已经单独进行了zero-center中心化处理，那么,

\[\bf{\sum_jz_j=\sum_jv_j=0}\\
\Downarrow \\
\bf{\frac{\partial{C}}{\partial{z_i}} \approx \frac{1}{NT^2}{(z_i-v_i)}}
\]

这样的话, 当T值最够大, 方法就变为求老师和学生的 logits 的 L2 距离了.

术语	说明
\(q^{soft}\)	老师模型的 softmax 输出软标签
\(q^{hard}\)	训练集 one-hot 硬标签
\(p^{soft}\)	学生模型的 softmax 输出软标签
\(p^{hard}\)	学生模型的 softmax 输出硬标签(T=1)

\[\bf {\text{loss_cross_entpopy} = \alpha \cdot T^2 \cdot q^{soft}\cdot \ln \left(p^\text{soft} \right) \\ \quad \quad \quad \quad + (1-\alpha) \cdot q^{hard}\cdot \ln \left(p^\text{hard} \right)}
\]

论文中发现通常给予硬标签损失函数 \(\color{red}{可忽略不计的较低权重}\) 可以获得最佳结果。由于软目标产生的梯度的大小为 \(\frac{1}{T^2}\)，因此当使用硬目标和软目标时，将它们乘以 \(T^2\) 是很重要的, 这确保软硬标签对梯度相对贡献在一个数量级。

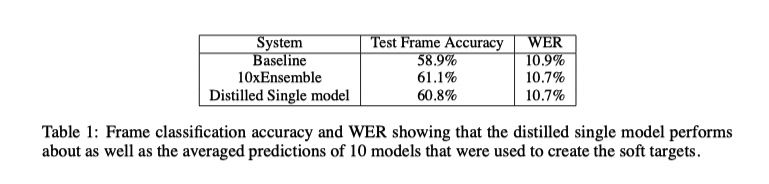
实验结果

思考

软标签交叉熵函数与 KL 散度的联系

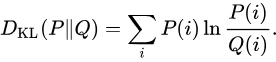
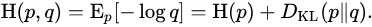
上式中, 由于 p 为老师的预测结果, 模型蒸馏时候, 老师模型被冻结, 从梯度反传来看, 软标签交叉熵函数等价于 KL 散度.

对于我而言, 这篇论文相对于 Do Deep Nets Really Need to be Deep? 贡献就在于, 将 L2距离和 KL 散度统一到一个公式中了, 由于到 T 足够大, KL 散度的梯度与 L2 距离的一样. 这篇论文中其他部分没有读懂, 没有看到其他想要的东西. 后面知识积累了有机会在看看有没有新感受吧.

蒸馏入门的话, 推荐 Do Deep Nets Really Need to be Deep? 这篇论文. 从实验分析来说, 各种分析都很到位, 分析的方式也是易读的, 容易理解. 就工程效果来看, 实际上Distilling the Knowledge in a Neural Network 这篇论文有效时候, T一般都挺大的, 那么KL 散度的实际的效果就是 L2 距离, 不如直接用 L2 距离, 理解上简单, 调节超参少, 效果也非常好.