【JDK】JDK源码分析-TreeMap(2)

前文「JDK源码分析-TreeMap(1)」分析了 TreeMap 的一些方法，本文分析其中的增删方法。这也是红黑树插入和删除节点的操作，由于相对复杂，因此单独进行分析。

插入操作

该操作其实就是红黑树的插入节点操作。前面分析过，红黑树是一种平衡二叉树，新增节点后可能导致其失去平衡，因此需要对其进行修复操作以维持其平衡性。插入操作的代码如下：

public V put(K key, V value) {
    Entry<K,V> t = root;
    // 若 root 节点为空，则直接插入（为根节点）
    if (t == null) {
        compare(key, key); // type (and possibly null) check
        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    // 拆分 Comparator 接口和 Comparable 接口（上文 getEntry 方法也是如此）
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                // 若key已存在，则替换其对应的value
                return t.setValue(value);
        } while (t != null);
    }
    else {
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    // 插入节点后的平衡性调整
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

对应的几种插入节点修复操作前文「数据结构与算法笔记（四）」已进行了分析，为了便于分析和理解代码，这里把图再贴一下（下图为关注节点的父节点是其祖父节点的左子节点的情况，在右边时操作类似）：

case1: 关注节点 a 的叔叔节点为红色

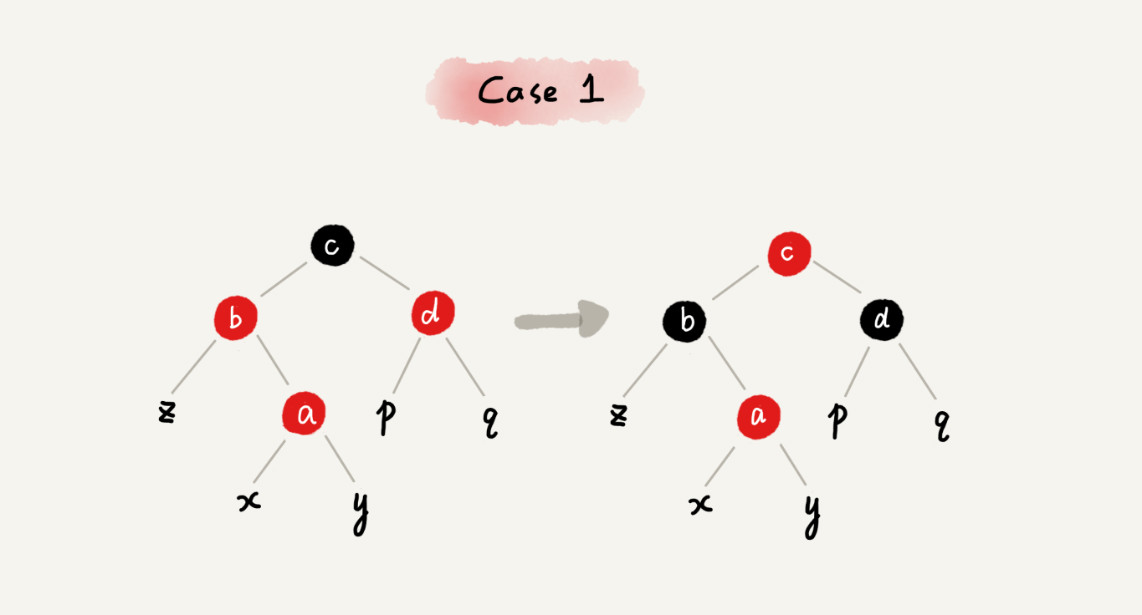
case2: 关注节点为 a，它的叔叔节点 d 是黑色，a 是其父节点 b 的右子节点

case3: 关注节点是 a，它的叔叔节点 d 是黑色，a 是其父节点 b 的左子节点

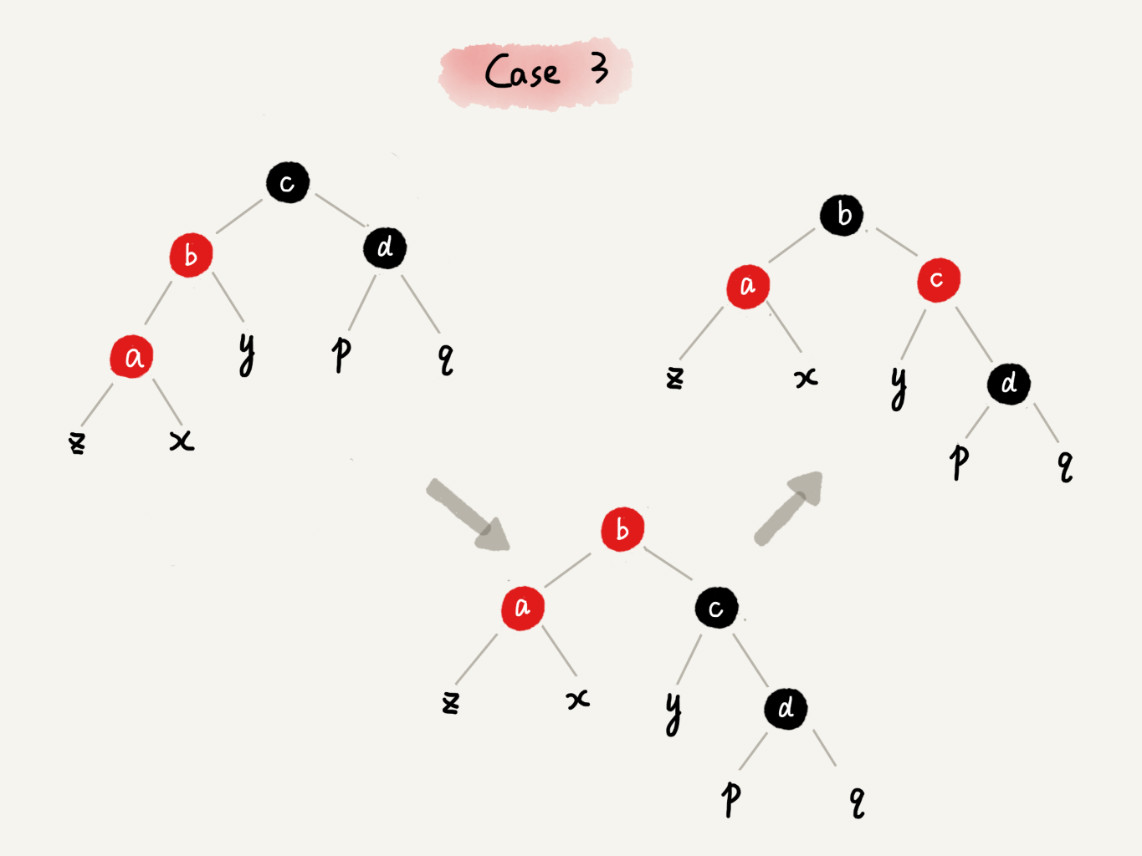
插入操作的平衡调整代码如下：

private void fixAfterInsertion(Entry<K,V> x) {
    // 新插入的节点为红色
    x.color = RED;
    // 只有在父节点为红色时需要进行插入修复操作
    while (x != null && x != root && x.parent.color == RED) {
        // 下面两种情况是左右对称的
        // x 的父节点是它祖父节点的左子节点
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // 叔叔节点
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            // case1
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                // case2
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                // case3
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        }
        // x 的父节点是它祖父节点的右子节点（与上面情况对称）
        else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    root.color = BLACK;
}

对称情况下的相应操作不再分析，其原理是类似的。

删除操作

remove() 方法：

public V remove(Object key) {
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;
    V oldValue = p.value;
    deleteEntry(p);
    return oldValue;
}

内部实现方法如下：

/**
 * Delete node p, and then rebalance the tree.
 */
private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size--;
    // If strictly internal, copy successor's element to p and then make p
    // point to successor.
    // 左右子树都不为空，寻找后继节点
    if (p.left != null && p.right != null) {
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    } // p has 2 children
    // Start fixup at replacement node, if it exists.
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);
    if (replacement != null) {
        // Link replacement to parent
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;
        // Null out links so they are OK to use by fixAfterDeletion.
        p.left = p.right = p.parent = null;
        // Fix replacement
        if (p.color == BLACK)
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // return if we are the only node.
        // 只有一个根节点
        root = null;
    } else { //  No children. Use self as phantom replacement and unlink.
        if (p.color == BLACK)
            fixAfterDeletion(p);
        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

几种删除操作情况如下（下图为关注节点为父节点的左子节点的情况，关注节点为父节点的右子节点情况时的操作对称）：

case1: 关注节点的兄弟节点是红色

case2: 关注节点的兄弟节点是黑色，且兄弟节点的子节点都是黑色

case3: 关注节点的兄弟节点是黑色，且左子节点是红色、右子节点是黑色

case4: 关注节点的兄弟节点是黑色，且右子节点是红色、左子节点是黑色

勘误：前文「数据结构与算法笔记（四）」对红黑树删除操作第四种情况的分析不够准确，近两天又参考了其他文章及代码，这里的 case4 是目前经分析认为比较准确的（符合 JDK 1.8 源码中 TreeMap 的实现思路）。

PS: 别人的资料也未必都正确，不可全信，包括本文，还是要持有怀疑精神的。

删除操作的平衡调整代码如下：

private void fixAfterDeletion(Entry<K,V> x) {
    // x 不为根节点，且颜色为黑色
    while (x != root && colorOf(x) == BLACK) {
        // x 是父节点的左子节点
        if (x == leftOf(parentOf(x))) {
            // 兄弟节点
            Entry<K,V> sib = rightOf(parentOf(x));
            // case1 待删除节点的兄弟节点为红色
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);
                setColor(parentOf(x), RED);
                rotateLeft(parentOf(x));
                sib = rightOf(parentOf(x));
            }
            // case2 待删除节点的兄弟节点的子节点都为黑色
            if (colorOf(leftOf(sib))  == BLACK && colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED);
                x = parentOf(x);
            } else {
                // case3 待删除节点的兄弟节点的左子节点为红色、右子节为黑色
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK);
                    setColor(sib, RED);
                    rotateRight(sib);
                    sib = rightOf(parentOf(x));
                }
                // case4 待删除节点的兄弟节点的左子节点为黑色、右子节为红色
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK);
                setColor(rightOf(sib), BLACK); //??
                rotateLeft(parentOf(x));
                x = root;
            }
        }
        // x 是父节点的右子节点（对称操作）
        else { // symmetric
            Entry<K,V> sib = leftOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);
                setColor(parentOf(x), RED);
                rotateRight(parentOf(x));
                sib = leftOf(parentOf(x));
            }
            if (colorOf(rightOf(sib)) == BLACK &&
                colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);
                x = parentOf(x);
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);
                    setColor(sib, RED);
                    rotateLeft(sib);
                    sib = leftOf(parentOf(x));
                }
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK);
                setColor(leftOf(sib), BLACK);
                rotateRight(parentOf(x));
                x = root;
            }
        }
    }
    setColor(x, BLACK);
}

插入和删除操作相对复杂，容易被绕晕，但其实也是有规律可循的。对比操作的图解，可以更容易分析和理解。

参考文章：

https://zhuanlan.zhihu.com/p/22800206

这篇文章介绍了红黑树的删除操作，逻辑清晰，推荐阅读。

相关阅读：

JDK源码分析-TreeMap(1)

数据结构与算法笔记（四）

Stay hungry, stay foolish.

PS: 本文首发于微信公众号【WriteOnRead】。