吴恩达课后作业学习2-week2-优化算法
参考:https://blog.csdn.net/u013733326/article/details/79907419
希望大家直接到上面的网址去查看代码,下面是本人的笔记
我们需要做以下几件事:
1. 分割数据集
2. 优化梯度下降算法:
2.1 不使用任何优化算法
2.2 mini-batch梯度下降法
2.3 使用具有动量的梯度下降算法
2.4 使用Adam算法
到目前为止,我们始终都是在使用梯度下降法学习,本文中,我们将使用一些更加高级的优化算法,利用这些优化算法,通常可以提高我们算法的收敛速度,并在最终得到更好的分离结果。这些方法可以加快学习速度,甚至可以为成本函数提供更好的最终值,在相同的结果下,有一个好的优化算法可以是等待几天和几个小时之间的差异。
1.导入包
# -*- coding: utf- -*- import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets import opt_utils #参见数据包或者在本文底部copy
import testCase #参见数据包或者在本文底部copy #%matplotlib inline #如果你用的是Jupyter Notebook请取消注释
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
警告:
/Users/user/pytorch/jupyter/-week2/opt_utils.py:: SyntaxWarning: assertion is always true, perhaps remove parentheses?
assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-])
/Users/user/pytorch/jupyter/-week2/opt_utils.py:: SyntaxWarning: assertion is always true, perhaps remove parentheses?
assert(parameters['W' + str(l)].shape == layer_dims[l], )
2.使用没有任何优化的梯度下降(GD,Gradient Descent)
之前使用的就是这个梯度下降方法,我们每一次循环都是对整个训练集进行学习,这叫做批量梯度下降(Batch Gradient Descent)
实现:
def update_parameters_with_gd(parameters,grads,learning_rate):
"""
使用梯度下降更新参数 参数:
parameters - 字典,包含了要更新的参数:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads - 字典,包含了每一个梯度值用以更新参数
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate - 学习率 返回值:
parameters - 字典,包含了更新后的参数
""" L = len(parameters) // 2 #神经网络的层数 #更新每个参数
for l in range(L):
parameters["W" + str(l +)] = parameters["W" + str(l + )] - learning_rate * grads["dW" + str(l + )]
parameters["b" + str(l +)] = parameters["b" + str(l + )] - learning_rate * grads["db" + str(l + )] return parameters
测试:
#测试update_parameters_with_gd
print("-------------测试update_parameters_with_gd-------------")
parameters , grads , learning_rate = testCase.update_parameters_with_gd_test_case()
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
返回:
-------------测试update_parameters_with_gd-------------
W1 = [[ 1.63535156 -0.62320365 -0.53718766]
[-1.07799357 0.85639907 -2.29470142]]
b1 = [[ 1.74604067]
[-0.75184921]]
W2 = [[ 0.32171798 -0.25467393 1.46902454]
[-2.05617317 -0.31554548 -0.3756023 ]
[ 1.1404819 -1.09976462 -0.1612551 ]]
b2 = [[-0.88020257]
[ 0.02561572]
[ 0.57539477]]
3.随机梯度下降(SGD)算法
由梯度下降算法演变来的还有随机梯度下降(SGD)算法。其相当于小批量梯度下降,但是和mini-batch不同的是其中每个小批量(mini-batch)仅有1个样本,和梯度下降不同的是你一次只能在一个训练样本上计算梯度,而不是在整个训练集上计算梯度。
#仅做比较,不运行。 #批量梯度下降,又叫梯度下降
X = data_input
Y = labels parameters = initialize_parameters(layers_dims)
for i in range(,num_iterations):
#前向传播
A,cache = forward_propagation(X,parameters)
#计算损失
cost = compute_cost(A,Y)
#反向传播
grads = backward_propagation(X,Y,cache)
#更新参数
parameters = update_parameters(parameters,grads) #随机梯度下降算法:
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in (,num_iterations):
for j in m: #m即样本数
#前向传播
A,cache = forward_propagation(X,parameters)
#计算成本
cost = compute_cost(A,Y)
#后向传播
grads = backward_propagation(X,Y,cache)
#更新参数
parameters = update_parameters(parameters,grads)
在随机梯度下降算法中,每次迭代中仅使用其中一个样本,当训练集很大时,使用随机梯度下降算法的运行速度会很快,但是会存在一定的波动,即有噪音。
在随机梯度下降中,在更新梯度之前,只使用1个训练样本。 当训练集较大时,随机梯度下降可以更快,但是参数会向最小值摆动,而不是平稳地收敛,我们来看一下比较图: 
4.小批量(mini-batch)梯度下降法
也是由梯度下降算法演变来的。小批量梯度下降法是一种综合了梯度下降法和随机梯度下降法的方法,在它的每次迭代中,既不是选择全部的数据来学习,也不是选择一个样本来学习,而是把所有的数据集分割为一小块一小块的来学习,它会随机选择一小块(mini-batch),块大小一般为2的n次方倍。一方面,充分利用的GPU的并行性,更一方面,不会让计算时间特别长,来看一下比较图: 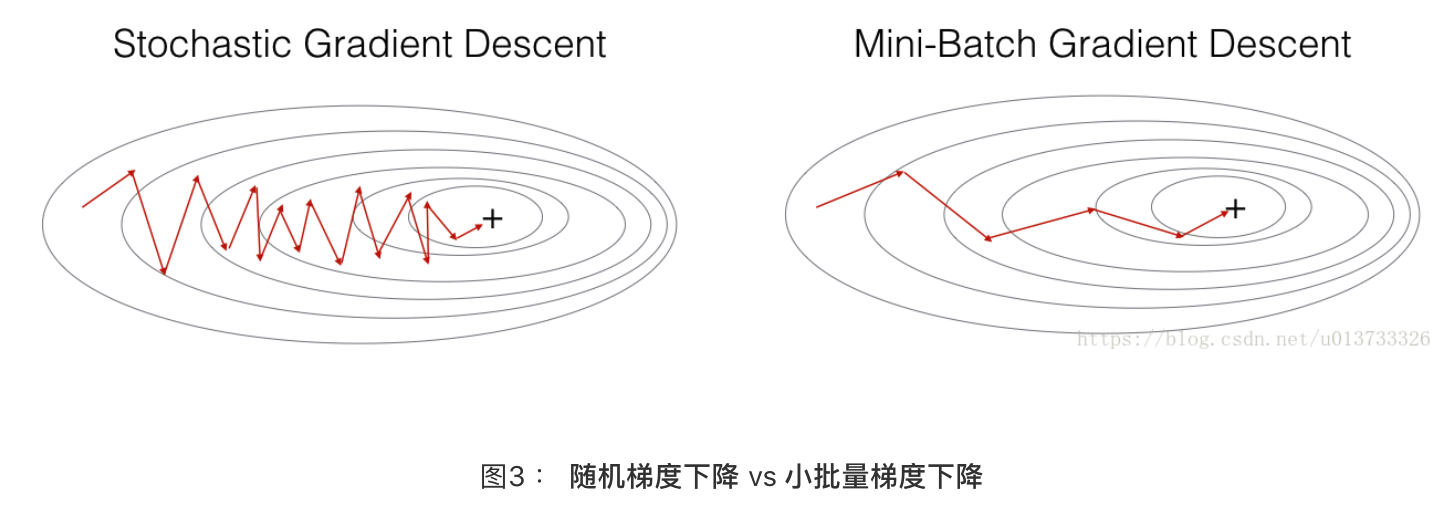
我们要使用mini-batch要经过两个步骤:
1. 把训练集打乱
2. 切分
def random_mini_batches(X,Y,mini_batch_size=,seed=):
"""
从(X,Y)中创建一个随机的mini-batch列表 参数:
X - 输入数据,维度为(输入节点数量,样本的数量)
Y - 对应的是X的标签,【 | 】(蓝|红),维度为(,样本的数量)
mini_batch_size - 每个mini-batch的样本数量 返回:
mini-bacthes - 一个同步列表,维度为(mini_batch_X,mini_batch_Y) """ np.random.seed(seed) #指定随机种子
m = X.shape[]
mini_batches = [] #第一步:打乱顺序
permutation = list(np.random.permutation(m)) #它会返回一个长度为m的随机数组,且里面的数是0到m-
shuffled_X = X[:,permutation] #将每一列的数据按permutation的顺序来重新排列。
shuffled_Y = Y[:,permutation].reshape((,m)) """
#博主注:
#如果你不好理解的话请看一下下面的伪代码,看看X和Y是如何根据permutation来打乱顺序的。
x = np.array([[,,,,,,,,],
[,,,,,,,,]])
y = np.array([[,,,,,,,,]]) random_mini_batches(x,y)
permutation= [, , , , , , , , ]
shuffled_X= [[ ]
[ ]]
shuffled_Y= [[ ]]
""" #第二步,分割
num_complete_minibatches = math.floor(m / mini_batch_size) #把你的训练集分割成多少份,请注意,如果值是99.,那么返回值是99,剩下的0.99会被舍弃
for k in range(,num_complete_minibatches):
mini_batch_X = shuffled_X[:,k * mini_batch_size:(k+)*mini_batch_size]
mini_batch_Y = shuffled_Y[:,k * mini_batch_size:(k+)*mini_batch_size]
"""
#博主注:
#如果你不好理解的话请单独执行下面的代码,它可以帮你理解一些。
a = np.array([[,,,,,,,,],
[,,,,,,,,],
[,,,,,,,,]])
k=
mini_batch_size=
print(a[:,*:(+)*]) #从第4列到第6列
'''
[[ ]
[ ]
[ ]]
'''
k=
print(a[:,*:(+)*]) #从第7列到第9列
'''
[[ ]
[ ]
[ ]]
''' #看一下每一列的数据你可能就会好理解一些
"""
mini_batch = (mini_batch_X,mini_batch_Y)
mini_batches.append(mini_batch) #如果训练集的大小刚好是mini_batch_size的整数倍,那么这里已经处理完了
#如果训练集的大小不是mini_batch_size的整数倍,那么最后肯定会剩下一些,我们要把它处理了
if m % mini_batch_size != :
#获取最后剩余的部分
mini_batch_X = shuffled_X[:,mini_batch_size * num_complete_minibatches:]
mini_batch_Y = shuffled_Y[:,mini_batch_size * num_complete_minibatches:] mini_batch = (mini_batch_X,mini_batch_Y)
mini_batches.append(mini_batch) return mini_batches
测试:
#测试random_mini_batches
print("-------------测试random_mini_batches-------------")
X_assess,Y_assess,mini_batch_size = testCase.random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess,Y_assess,mini_batch_size) print("第1个mini_batch_X 的维度为:",mini_batches[][].shape)
print("第1个mini_batch_Y 的维度为:",mini_batches[][].shape)
print("第2个mini_batch_X 的维度为:",mini_batches[][].shape)
print("第2个mini_batch_Y 的维度为:",mini_batches[][].shape)
print("第3个mini_batch_X 的维度为:",mini_batches[][].shape)
print("第3个mini_batch_Y 的维度为:",mini_batches[][].shape)
返回:
-------------测试random_mini_batches-------------
第1个mini_batch_X 的维度为: (, )
第1个mini_batch_Y 的维度为: (, )
第2个mini_batch_X 的维度为: (, )
第2个mini_batch_Y 的维度为: (, )
第3个mini_batch_X 的维度为: (, )
第3个mini_batch_Y 的维度为: (, )
5.包含动量的梯度下降——momentum
小批量梯度下降的路径将“振荡地”走向收敛,使用动量可以减少这些振荡,动量考虑了过去的梯度以平滑更新, 我们将把以前梯度的方向存储在变量v中,从形式上讲,这将是前面的梯度的指数加权平均值。
既然我们要影响梯度的方向,而梯度需要使用到dW和db,那么我们就要建立一个和dW和db相同结构的变量来影响他们,我们现在来进行初始化:
为对应的参数初始化维度相同的值为0的v:
def initialize_velocity(parameters): #初始化值为0的v
"""
初始化速度,velocity是一个字典:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values:与相应的梯度/参数维度相同的值为零的矩阵。
参数:
parameters - 一个字典,包含了以下参数:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v - 一个字典变量,包含了以下参数:
v["dW" + str(l)] = dWl的速度
v["db" + str(l)] = dbl的速度 """
L = len(parameters) // 2 #神经网络的层数
v = {} for l in range(L):
v["dW" + str(l + )] = np.zeros_like(parameters["W" + str(l + )])
v["db" + str(l + )] = np.zeros_like(parameters["b" + str(l + )]) return v
测试:
#测试initialize_velocity
print("-------------测试initialize_velocity-------------")
parameters = testCase.initialize_velocity_test_case()
v = initialize_velocity(parameters) print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
返回:
-------------测试initialize_velocity-------------
v["dW1"] = [[. . .]
[. . .]]
v["db1"] = [[.]
[.]]
v["dW2"] = [[. . .]
[. . .]
[. . .]]
v["db2"] = [[.]
[.]
[.]]

实现使用该优化算法对参数进行优化:
def update_parameters_with_momentun(parameters,grads,v,beta,learning_rate):
"""
使用动量更新参数
参数:
parameters - 一个字典类型的变量,包含了以下字段:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
grads - 一个包含梯度值的字典变量,具有以下字段:
grads["dW" + str(l)] = dWl
grads["db" + str(l)] = dbl
v - 包含当前速度的字典变量,具有以下字段:
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
beta - 超参数,动量,实数
learning_rate - 学习率,实数
返回:
parameters - 更新后的参数字典
v - 包含了更新后的速度变量
"""
L = len(parameters) // 2
for l in range(L):
#计算速度
v["dW" + str(l + )] = beta * v["dW" + str(l + )] + ( - beta) * grads["dW" + str(l + )]
v["db" + str(l + )] = beta * v["db" + str(l + )] + ( - beta) * grads["db" + str(l + )] #更新参数
parameters["W" + str(l + )] = parameters["W" + str(l + )] - learning_rate * v["dW" + str(l + )]
parameters["b" + str(l + )] = parameters["b" + str(l + )] - learning_rate * v["db" + str(l + )] return parameters,v
测试:
#测试update_parameters_with_momentun
print("-------------测试update_parameters_with_momentun-------------")
parameters,grads,v = testCase.update_parameters_with_momentum_test_case()
update_parameters_with_momentun(parameters,grads,v,beta=0.9,learning_rate=0.01) print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
返回:
-------------测试update_parameters_with_momentun-------------
W1 = [[ 1.62544598 -0.61290114 -0.52907334]
[-1.07347112 0.86450677 -2.30085497]]
b1 = [[ 1.74493465]
[-0.76027113]]
W2 = [[ 0.31930698 -0.24990073 1.4627996 ]
[-2.05974396 -0.32173003 -0.38320915]
[ 1.13444069 -1.0998786 -0.1713109 ]]
b2 = [[-0.87809283]
[ 0.04055394]
[ 0.58207317]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157]
[0.16598022]
[0.07420442]]
需要注意的是速度v
是用0来初始化的,因此,该算法需要经过几次迭代才能把速度提升上来并开始跨越更大步伐。当beta=0时,该算法相当于是没有使用momentum算法的标准的梯度下降算法。当beta越大的时候,说明平滑的作用越明显。通常0.9是比较合适的值。
那如何才能在开始的时候就保持很快的速度向最小误差那里前进呢?我们来看看下面的Adam算法。
6.Adam算法
Adam算法是训练神经网络中最有效的算法之一,它是RMSProp算法与Momentum算法的结合体。我们来看看它都干了些什么吧~
1. 计算以前的梯度的指数加权平均值,并将其存储在变量v(偏差校正前)和vcorrected(偏差校正后)中。
2. 计算以前梯度的平方的指数加权平均值,并将其存储在变量s(偏差校正前)和scorrected(偏差校正后)中。
3. 根据1和2更新参数。 
初始化,也为0:
def initialize_adam(parameters):
"""
初始化v和s,它们都是字典类型的变量,都包含了以下字段:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values:与对应的梯度/参数相同维度的值为零的numpy矩阵 参数:
parameters - 包含了以下参数的字典变量:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v - 包含梯度的指数加权平均值,字段如下:
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s - 包含平方梯度的指数加权平均值,字段如下:
s["dW" + str(l)] = ...
s["db" + str(l)] = ... """ L = len(parameters) //
v = {}
s = {} for l in range(L):
v["dW" + str(l + )] = np.zeros_like(parameters["W" + str(l + )])
v["db" + str(l + )] = np.zeros_like(parameters["b" + str(l + )]) s["dW" + str(l + )] = np.zeros_like(parameters["W" + str(l + )])
s["db" + str(l + )] = np.zeros_like(parameters["b" + str(l + )]) return (v,s)
测试:
#测试initialize_adam
print("-------------测试initialize_adam-------------")
parameters = testCase.initialize_adam_test_case()
v,s = initialize_adam(parameters) print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
print('s["dW1"] = ' + str(s["dW1"]))
print('s["db1"] = ' + str(s["db1"]))
print('s["dW2"] = ' + str(s["dW2"]))
print('s["db2"] = ' + str(s["db2"]))
返回:
-------------测试initialize_adam-------------
v["dW1"] = [[. . .]
[. . .]]
v["db1"] = [[.]
[.]]
v["dW2"] = [[. . .]
[. . .]
[. . .]]
v["db2"] = [[.]
[.]
[.]]
s["dW1"] = [[. . .]
[. . .]]
s["db1"] = [[.]
[.]]
s["dW2"] = [[. . .]
[. . .]
[. . .]]
s["db2"] = [[.]
[.]
[.]]
参数初始化完成了,我们就根据上面的公式来更新参数:
def update_parameters_with_adam(parameters,grads,v,s,t,learning_rate=0.01,beta1=0.9,beta2=0.999,epsilon=1e-):
"""
使用Adam更新参数 参数:
parameters - 包含了以下字段的字典:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads - 包含了梯度值的字典,有以下key值:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v - Adam的变量,第一个梯度的移动平均值,是一个字典类型的变量
s - Adam的变量,平方梯度的移动平均值,是一个字典类型的变量
t - 当前迭代的次数
learning_rate - 学习率
beta1 - 动量,超参数,用于第一阶段,使得曲线的Y值不从0开始(参见天气数据的那个图)
beta2 - RMSprop的一个参数,超参数
epsilon - 防止除零操作(分母为0) 返回:
parameters - 更新后的参数
v - 第一个梯度的移动平均值,是一个字典类型的变量
s - 平方梯度的移动平均值,是一个字典类型的变量
"""
L = len(parameters) //
v_corrected = {} #偏差修正后的值
s_corrected = {} #偏差修正后的值 for l in range(L):
#梯度的移动平均值,输入:"v , grads , beta1",输出:" v "
v["dW" + str(l + )] = beta1 * v["dW" + str(l + )] + ( - beta1) * grads["dW" + str(l + )]
v["db" + str(l + )] = beta1 * v["db" + str(l + )] + ( - beta1) * grads["db" + str(l + )] #计算第一阶段的偏差修正后的估计值,输入"v , beta1 , t" , 输出:"v_corrected"
v_corrected["dW" + str(l + )] = v["dW" + str(l + )] / ( - np.power(beta1,t))
v_corrected["db" + str(l + )] = v["db" + str(l + )] / ( - np.power(beta1,t)) #计算平方梯度的移动平均值,输入:"s, grads , beta2",输出:"s"
s["dW" + str(l + )] = beta2 * s["dW" + str(l + )] + ( - beta2) * np.square(grads["dW" + str(l + )])
s["db" + str(l + )] = beta2 * s["db" + str(l + )] + ( - beta2) * np.square(grads["db" + str(l + )]) #计算第二阶段的偏差修正后的估计值,输入:"s , beta2 , t",输出:"s_corrected"
s_corrected["dW" + str(l + )] = s["dW" + str(l + )] / ( - np.power(beta2,t))
s_corrected["db" + str(l + )] = s["db" + str(l + )] / ( - np.power(beta2,t)) #更新参数,输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
parameters["W" + str(l + )] = parameters["W" + str(l + )] - learning_rate * (v_corrected["dW" + str(l + )] / np.sqrt(s_corrected["dW" + str(l + )] + epsilon))
parameters["b" + str(l + )] = parameters["b" + str(l + )] - learning_rate * (v_corrected["db" + str(l + )] / np.sqrt(s_corrected["db" + str(l + )] + epsilon)) return (parameters,v,s)
测试:
#测试update_with_parameters_with_adam
print("-------------测试update_with_parameters_with_adam-------------")
parameters , grads , v , s = testCase.update_parameters_with_adam_test_case()
update_parameters_with_adam(parameters,grads,v,s,t=) print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
print('s["dW1"] = ' + str(s["dW1"]))
print('s["db1"] = ' + str(s["db1"]))
print('s["dW2"] = ' + str(s["dW2"]))
print('s["db2"] = ' + str(s["db2"]))
返回:
-------------测试update_with_parameters_with_adam-------------
W1 = [[ 1.63178673 -0.61919778 -0.53561312]
[-1.08040999 0.85796626 -2.29409733]]
b1 = [[ 1.75225313]
[-0.75376553]]
W2 = [[ 0.32648046 -0.25681174 1.46954931]
[-2.05269934 -0.31497584 -0.37661299]
[ 1.14121081 -1.09245036 -0.16498684]]
b2 = [[-0.88529978]
[ 0.03477238]
[ 0.57537385]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157]
[0.16598022]
[0.07420442]]
s["dW1"] = [[0.00121136 0.00131039 0.00081287]
[0.0002525 0.00081154 0.00046748]]
s["db1"] = [[1.51020075e-05]
[8.75664434e-04]]
s["dW2"] = [[7.17640232e-05 2.81276921e-04 4.78394595e-04]
[1.57413361e-04 4.72206320e-04 7.14372576e-04]
[4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"] = [[5.49507194e-05]
[2.75494327e-03]
[5.50629536e-04]]
上面已经做好了三个优化器,下面就使用看看效果怎么样
7.测试
1)下载数据
train_X, train_Y = opt_utils.load_dataset(is_plot=True)
图示为:
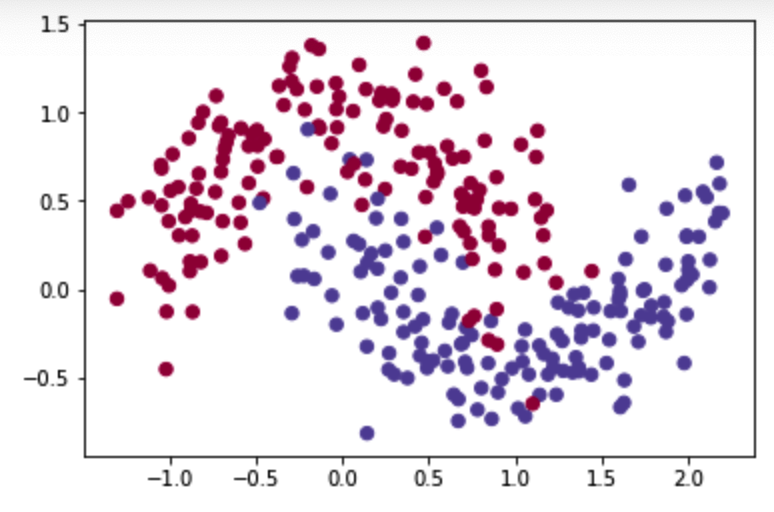
之前已经实现过了一个三层的神经网络,我们将分别用它来测试我们的优化器的优化效果,模型为:
def model(X,Y,layers_dims,optimizer,learning_rate=0.0007,
mini_batch_size=,beta=0.9,beta1=0.9,beta2=0.999,
epsilon=1e-,num_epochs=,print_cost=True,is_plot=True): """
可以运行在不同优化器模式下的3层神经网络模型。 参数:
X - 输入数据,维度为(,输入的数据集里面样本数量)
Y - 与X对应的标签
layers_dims - 包含层数和节点数量的列表
optimizer - 字符串类型的参数,用于选择优化类型,【 "gd" | "momentum" | "adam" 】
learning_rate - 学习率
mini_batch_size - 每个小批量数据集的大小
beta - 用于动量优化的一个超参数
beta1 - 用于计算梯度后的指数衰减的估计的超参数
beta1 - 用于计算平方梯度后的指数衰减的估计的超参数
epsilon - 用于在Adam中避免除零操作的超参数,一般不更改
num_epochs - 整个训练集的遍历次数,(视频2.9学习率衰减,1分55秒处,视频中称作“代”),相当于之前的num_iteration
print_cost - 是否打印误差值,每遍历1000次数据集打印一次,但是每100次记录一个误差值,又称每1000代打印一次
is_plot - 是否绘制出曲线图 返回:
parameters - 包含了学习后的参数 """
L = len(layers_dims)
costs = []
t = #每学习完一个minibatch就增加1
seed = #随机种子 #初始化参数
parameters = opt_utils.initialize_parameters(layers_dims) #选择优化器
if optimizer == "gd":
pass #不使用任何优化器,直接使用梯度下降法
elif optimizer == "momentum":
v = initialize_velocity(parameters) #使用动量
elif optimizer == "adam":
v, s = initialize_adam(parameters)#使用Adam优化
else:
print("optimizer参数错误,程序退出。")
exit() #开始学习
for i in range(num_epochs):
#定义随机 minibatches,我们在每次遍历数据集之后增加种子以重新排列数据集,使每次数据的顺序都不同
seed = seed +
minibatches = random_mini_batches(X,Y,mini_batch_size,seed) for minibatch in minibatches:
#选择一个minibatch
(minibatch_X,minibatch_Y) = minibatch #前向传播
A3 , cache = opt_utils.forward_propagation(minibatch_X,parameters) #计算误差
cost = opt_utils.compute_cost(A3 , minibatch_Y) #反向传播
grads = opt_utils.backward_propagation(minibatch_X,minibatch_Y,cache) #更新参数
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentun(parameters,grads,v,beta,learning_rate)
elif optimizer == "adam":
t = t +
parameters , v , s = update_parameters_with_adam(parameters,grads,v,s,t,learning_rate,beta1,beta2,epsilon)
#记录误差值
if i % == :
costs.append(cost)
#是否打印误差值
if print_cost and i % == :
print("第" + str(i) + "次遍历整个数据集,当前误差值:" + str(cost))
#是否绘制曲线图
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show() return parameters
2)首先测试GD优化器
#使用普通的梯度下降
layers_dims = [train_X.shape[],,,]
parameters = model(train_X, train_Y, layers_dims, optimizer="gd",is_plot=True)
返回:
第0次遍历整个数据集,当前误差值:0.690735512291113
第1000次遍历整个数据集,当前误差值:0.6852725328458241
第2000次遍历整个数据集,当前误差值:0.6470722240719003
第3000次遍历整个数据集,当前误差值:0.6195245549970402
第4000次遍历整个数据集,当前误差值:0.5765844355950944
第5000次遍历整个数据集,当前误差值:0.6072426395968576
第6000次遍历整个数据集,当前误差值:0.5294033317684576
第7000次遍历整个数据集,当前误差值:0.46076823985930115
第8000次遍历整个数据集,当前误差值:0.465586082399045
第9000次遍历整个数据集,当前误差值:0.4645179722167684
图示:

绘制分类图:
def plot_decision_boundary(model, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[, :].min() - , X[, :].max() +
y_min, y_max = X[, :].min() - , X[, :].max() +
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[, :], X[, :], c=np.squeeze(y), cmap=plt.cm.Spectral) #更改
plt.show()
运行:
#预测
preditions = opt_utils.predict(train_X,train_Y,parameters) #绘制分类图
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-, 1.5])
plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
返回:
Accuracy: 0.7966666666666666
图示:
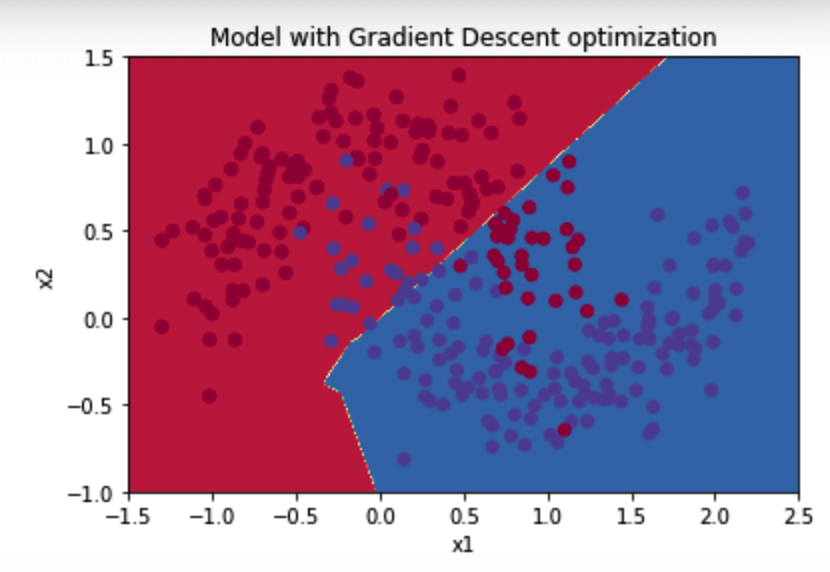
3)momentum优化器
因为这个例子比较简单,使用动量效果很小,但对于更复杂的问题,你可能会看到更好的效果。
layers_dims = [train_X.shape[],,,]
#使用动量的梯度下降
parameters = model(train_X, train_Y, layers_dims, beta=0.9,optimizer="momentum",is_plot=True)
返回:
第0次遍历整个数据集,当前误差值:0.6907412988351506
第1000次遍历整个数据集,当前误差值:0.6853405261267578
第2000次遍历整个数据集,当前误差值:0.6471448370095255
第3000次遍历整个数据集,当前误差值:0.6195943032076023
第4000次遍历整个数据集,当前误差值:0.5766650344073023
第5000次遍历整个数据集,当前误差值:0.607323821900647
第6000次遍历整个数据集,当前误差值:0.5294761758786997
第7000次遍历整个数据集,当前误差值:0.46093619004872366
第8000次遍历整个数据集,当前误差值:0.465780093701272
第9000次遍历整个数据集,当前误差值:0.4647395967922748
图示:

绘制分类图:
#预测
preditions = opt_utils.predict(train_X,train_Y,parameters) #绘制分类图
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-, 1.5])
plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
返回:
Accuracy: 0.7966666666666666
图示:
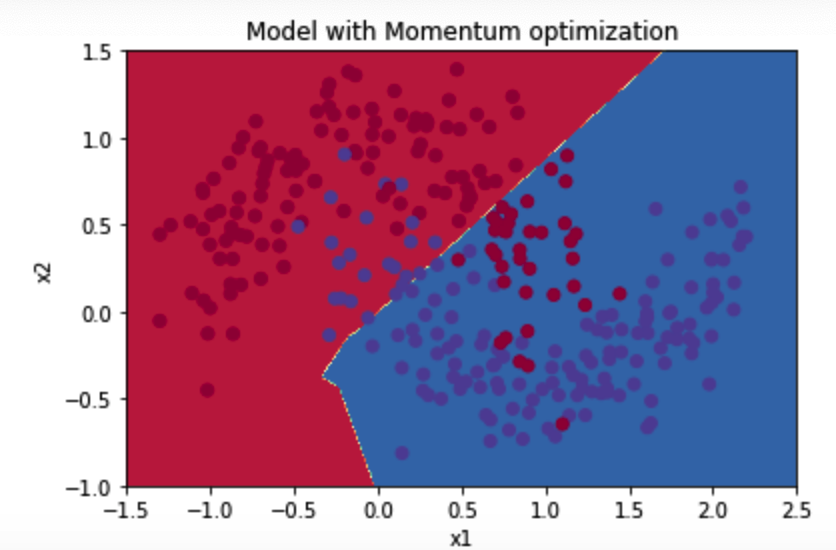
4)Adam优化器
layers_dims = [train_X.shape[], , , ]
#使用Adam优化的梯度下降
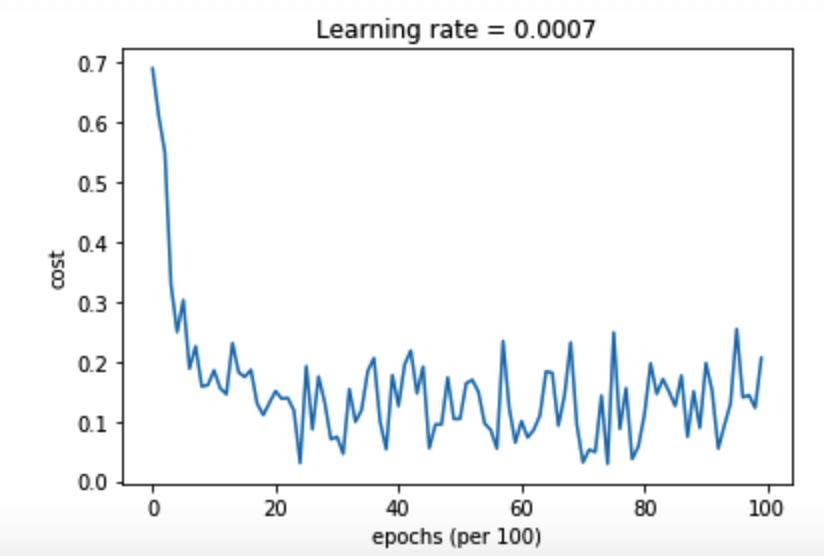
parameters = model(train_X, train_Y, layers_dims,optimizer="adam",is_plot=True)
返回:
第0次遍历整个数据集,当前误差值:0.6905522446113365
第1000次遍历整个数据集,当前误差值:0.18550136438550568
第2000次遍历整个数据集,当前误差值:0.15083046575253206
第3000次遍历整个数据集,当前误差值:0.07445438570997176
第4000次遍历整个数据集,当前误差值:0.1259591565133716
第5000次遍历整个数据集,当前误差值:0.10434443534245481
第6000次遍历整个数据集,当前误差值:0.10067637504120656
第7000次遍历整个数据集,当前误差值:0.031652030135115604
第8000次遍历整个数据集,当前误差值:0.111972731312442
第9000次遍历整个数据集,当前误差值:0.19794007152465481
图示:
绘制分类图:
#预测
preditions = opt_utils.predict(train_X,train_Y,parameters) #绘制分类图
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-, 1.5])
plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
返回:
Accuracy: 0.94
图示为:

总结:
优化算法 准确度 曲线平滑度
梯度下降 79.7% 震荡
具有动量的梯度下降算法 79.7% 震荡
Adam优化后的梯度下降 94% 平滑
具有动量的梯度下降通常可以有很好的效果,但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。
另一方面,Adam明显优于小批量梯度下降和具有动量的梯度下降,如果在这个简单的模型上运行更多时间的数据集,这三种方法都会产生非常好的结果,然而,我们已经看到Adam收敛得更快。
Adam的一些优点包括相对较低的内存要求(虽然比梯度下降和动量下降更高)和通常运作良好,即使对参数进行微调(除了学习率α)
吴恩达课后作业学习2-week2-优化算法的更多相关文章
- 吴恩达课后作业学习1-week4-homework-two-hidden-layer -1
参考:https://blog.csdn.net/u013733326/article/details/79767169 希望大家直接到上面的网址去查看代码,下面是本人的笔记 两层神经网络,和吴恩达课 ...
- 吴恩达课后作业学习1-week4-homework-multi-hidden-layer -2
参考:https://blog.csdn.net/u013733326/article/details/79767169 希望大家直接到上面的网址去查看代码,下面是本人的笔记 实现多层神经网络 1.准 ...
- 吴恩达课后作业学习2-week1-1 初始化
参考:https://blog.csdn.net/u013733326/article/details/79847918 希望大家直接到上面的网址去查看代码,下面是本人的笔记 初始化.正则化.梯度校验 ...
- 吴恩达课后作业学习2-week1-2正则化
参考:https://blog.csdn.net/u013733326/article/details/79847918 希望大家直接到上面的网址去查看代码,下面是本人的笔记 4.正则化 1)加载数据 ...
- 吴恩达课后作业学习2-week3-tensorflow learning-1-例子学习
参考:https://blog.csdn.net/u013733326/article/details/79971488 使用TensorFlow构建你的第一个神经网络 我们将会使用TensorFlo ...
- 吴恩达课后作业学习1-week2-homework-logistic
参考:https://blog.csdn.net/u013733326/article/details/79639509 希望大家直接到上面的网址去查看代码,下面是本人的笔记 搭建一个能够 “识别猫” ...
- 吴恩达课后作业学习1-week3-homework-one-hidden-layer
参考:https://blog.csdn.net/u013733326/article/details/79702148 希望大家直接到上面的网址去查看代码,下面是本人的笔记 建立一个带有隐藏层的神经 ...
- 吴恩达课后作业学习2-week3-tensorflow learning-1-基本概念
参考:https://blog.csdn.net/u013733326/article/details/79971488 希望大家直接到上面的网址去查看代码,下面是本人的笔记 到目前为止,我们一直在 ...
- 吴恩达课后作业学习2-week1-3梯度校验
参考:https://blog.csdn.net/u013733326/article/details/79847918 希望大家直接到上面的网址去查看代码,下面是本人的笔记 5.梯度校验 在我们执行 ...
随机推荐
- java.net.ProtocolException:unexpected end of stream
原因:php 给android 写接口出现java.net.ProtocolException:unexpected end of stream,查找android方面原因时发现数据超长 ,发现htm ...
- element vue Array数组和Map对象的添加与删除
使用场景: 一个后台系统中, 管理员要配置自定义字段后台要生成id和title,其他角色要使用自定义字段的表单, 添加数据, 但是每个要填写的对象的id 和title都是无法固定的,因此页面显示的ti ...
- 使用FileReader接口读取文件内容
如果想要读取或浏览文件,则需要通过FileReader接口,该接口不仅可以读取图片文件,还可以读取文本或二进制文件,同时,根据该接口提供的事件与方法,可以动态侦察文件读取时的详细状态,接下来,我们详细 ...
- ionic APP二维码插件 地址
二维码插件地址第一个 https://github.com/kyocn/BarcodeScanner git网址 下载网址 https://github.com/kyocn/BarcodeSc ...
- 苹果手机怎么屏幕录屏 ios10怎么录屏
手机录屏已经现阶段经常使用的功能,有些人喜欢在手机上看视频,看直播.但是有时候看到很精彩的视频,就想要录制下来,这个时候可以采取录屏的方式.那么就涉及到手机怎么录制屏幕视频了?想用苹果手机把手机屏幕录 ...
- net core webApi返回值
1 多个参数采用结构的形式,如class xyz 2 返回值使用IActionResult 控制,不能使用httpRequestMessage类型 3 url为路由名称+Controller前缀 如下 ...
- 18.Odoo产品分析 (二) – 商业板块(10) – 电子商务(2)
查看Odoo产品分析系列--目录 接上一篇Odoo产品分析 (二) – 商业板块(10) – 电子商务(1) 6. 高级属性 除了我们到目前为止已经覆盖基本选项,Odoo在产品页面还提供了一些高级选项 ...
- 使用fiddler抓包手机请求数据
1.启动Fiddler,打开菜单栏中的 Tools > Fiddler Options,打开“Fiddler Options”对话框. 2.在Fiddler Options”对话框切换到“Con ...
- C#多线程图片爬虫
写了个简单的多线程图片爬虫,整理一下.数据已经爬下来了,图片URL需要自行拼接,首先从Lawyers表中取的RawData字段,RawData中有一个list字段是json格式的数据,需要的只是lis ...
- Big Endian 和 Little Endian 模式的区别
谈到字节序的问题,必然牵涉到两大CPU派系.那就是Motorola的PowerPC系列CPU和Intel的x86系列CPU.PowerPC系列采用big endian方式存储数据,而x86系列则采用l ...
