洛谷P1712 区间

题意：给你n个区间，从中选择m个，使得它们有交，且最长与最短区间的差值最小。

解：这道题我想了好多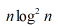的，nlog²n错的，nlogn错的，最后终于想出nlogn的了......

把区间按照长度排序，然后依次在线段树上加。

如果某一次等于m了，那么一个一个删，删到小于m的时候，更新答案。

证明：那些之前的区间如果想要成为答案，那么必须是和比当前这个还靠前的区间来组成。

这样的话当到这一个时，之前的要么被计算，要么不会更优。故可以删掉。

 #include <cstdio>
 #include <algorithm>

 const int N = , INF = 0x3f3f3f3f;

 int sum[N << ], large[N << ], tag[N << ], X[N << ];

 struct ITV {
     int r, l, len;
     inline bool operator <(const ITV &w) const {
        return len < w.len;
     }
 }a[N];

 inline void pushup(int o) {
     int ls = o << ;
     int rs = ls | ;
     sum[o] = sum[ls] + sum[rs];
     large[o] = std::max(large[ls], large[rs]);
     return;
 }

 inline void pushdown(int l, int r, int o) {
     if(tag[o]) {
         int ls = o << ;
         int rs = ls | ;
         int mid = (l + r) >> ;
         tag[ls] += tag[o];
         tag[rs] += tag[o];
         sum[ls] += (mid - l + ) * tag[o];
         sum[rs] += (r - mid) * tag[o];
         large[ls] += tag[o];
         large[rs] += tag[o];
         tag[o] = ;
     }
     return;
 }

 inline void add(int L, int R, int v, int l, int r, int o) {
     if(L <= l && r <= R) {
         tag[o] += v;
         sum[o] += v * (r - l + );
         large[o] += v;
         return;
     }
     pushdown(l, r, o);
     int mid = (l + r) >> ;
     if(L <= mid) {
         add(L, R, v, l, mid, o << );
     }
     if(mid < R) {
         add(L, R, v, mid + , r, o <<  | );
     }
     pushup(o);
     return;
 }

 int main() {

     int n, m;
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++) {
         scanf("%d%d", &a[i].l, &a[i].r);
         a[i].len = a[i].r - a[i].l;
         X[i << ] = a[i].l;
         X[(i << ) - ] = a[i].r;
     }
     std::sort(a + , a + n + );
     std::sort(X + , X + (n << ) + );
     int t = std::unique(X + , X + (n << ) + ) - X - ;
     int j = , ans = INF;
     for(int i = ; i <= n; i++) {
         a[i].l = std::lower_bound(X + , X + t + , a[i].l) - X;
         a[i].r = std::lower_bound(X + , X + t + , a[i].r) - X;
         add(a[i].l, a[i].r, , , t, );
         while(large[] >= m) {
             add(a[j].l, a[j].r, -, , t, );
             //printf("large[1] = %d  ans = %d \n i = %d j = %d \n", large[1], ans, i, j);
             ans = std::min(ans, a[i].len - a[j].len);
             j++;
         }
     }
     if(ans == INF) {
         ans = -;
     }
     printf("%d\n", ans);
     return ;
 }

AC代码

这个sum其实是不必要的。

然后我还用动态开点写了一发......被卡空间了。

 #include <cstdio>
 #include <algorithm>

 const int N = , INF = 0x3f3f3f3f;

 int large[N * ], tag[N * ], root, ls[N * ], rs[N * ], tot;

 struct ITV {
     int r, l, len;
     inline bool operator <(const ITV &w) const {
        return len < w.len;
     }
 }a[N];

 inline void pushup(int o) {
     large[o] = std::max(large[ls[o]], large[rs[o]]);
     return;
 }

 inline void pushdown(int l, int r, int o) {
     if(tag[o]) {
         int mid = (l + r) >> ;
         if(ls[o]) {
             large[ls[o]] += tag[o];
             tag[ls[o]] += tag[o];
         }
         if(rs[o]) {
             large[rs[o]] += tag[o];
             tag[rs[o]] += tag[o];
         }
         tag[o] = ;
     }
     return;
 }

 inline void add(int L, int R, int v, int l, int r, int &o) {
     if(!o) {
         o = ++tot;
     }
     if(L <= l && r <= R) {
         tag[o] += v;
         large[o] += v;
         return;
     }
     if(!ls[o]) {
         ls[o] = ++tot;
     }
     if(!rs[o]) {
         rs[o] = ++tot;
     }
     pushdown(l, r, o);
     int mid = (l + r) >> ;
     if(L <= mid) {
         add(L, R, v, l, mid, ls[o]);
     }
     if(mid < R) {
         add(L, R, v, mid + , r, rs[o]);
     }
     pushup(o);
     return;
 }

 int main() {

     int n, m, lm = ;
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++) {
         scanf("%d%d", &a[i].l, &a[i].r);
         a[i].len = a[i].r - a[i].l;
         lm = std::max(lm, a[i].r);
     }
     std::sort(a + , a + n + );
     int j = , ans = INF;
     for(int i = ; i <= n; i++) {
         add(a[i].l, a[i].r, , , lm, root);
         while(large[] >= m) {
             add(a[j].l, a[j].r, -, , lm, root);
             //printf("large[1] = %d  ans = %d \n i = %d j = %d \n", large[1], ans, i, j);
             ans = std::min(ans, a[i].len - a[j].len);
             j++;
         }
     }
     if(ans == INF) {
         ans = -;
     }
     printf("%d\n", ans);
     return ;
 }

95分动态开点