闵可夫斯基和（Mincowsky sum）

一、概述

官方定义：两个图形A,B的闵可夫斯基和C={a+b|a∈A,b∈B}
通俗一点：从原点向图形A内部的每一个点做向量，将图形B沿每个向量移动，所有的最终位置的并便是闵可夫斯基和（具有交换律）

例如，平面上有两个三角形，其坐标分别为A={(1,0),(0,1),(0,-1)}及B = {(0, 0), (1, 1), (1, −1)}，则其闵可夫斯基和为A + B = {(1, 0), (2, 1), (2, −1), (0, 1), (1, 2), (1, 0), (0, −1), (1, 0), (1, −2)}。若推广至流形的连续集，闵可夫斯基和从几何上的直观体现即是A集合沿B的边际连续运动一周扫过的区域与B集合本身的并集，也可以使B沿着A的边界连续运动扫过区域与A自身的并集。

本文只讨论凸包的闵可夫斯基和。如下图，粉色区域便是三角形和一个不规则四边形的闵可夫斯基和

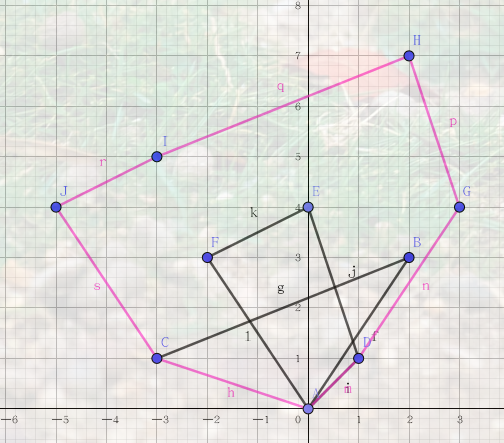
二、怎么求

闵可夫斯基和的边是由两凸包构成的
也就是说把两凸包的边极角排序后直接顺次连起来就是闵可夫斯基和

凸包肯定会存在于A的凸包+B的凸包上。

我们可以给这个两个点集做一次凸包，然后再从这两个点集中分别x最小中y最小的点开始。

出来之后，可能是这样的。

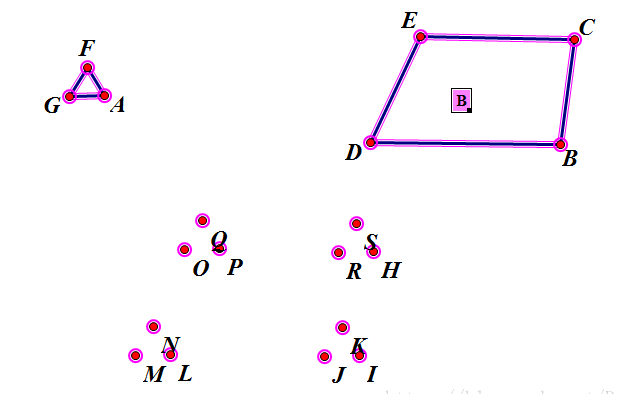
就是M点开始，我们进行找点运动。

可以感性理解：下一个凸包上的点是或者。前提是已经做好凸包，也就是说，点是逆时针排布的。

所以这样，我们就可以做出来了。

三、算法

求凸包之间的闵可夫斯基和的方法。
把两个凸包的每一条向量都抠出来，按照极角序排序构成新凸包即可。
注意点和向量的去重(向量相同斜率去重)。

还有个地方可以提一下：求多个凸包的闵可夫斯基和的时候可以直接全把边拿出来一块求，没有必要两个两个求。
具体实现的时候，找出最高且最靠左的点。

先把这个点加入答案，从这个点开始把所有向量遍历一遍，最后去掉最后一个点即可(最后这个点会和第一个点重合)。
下面是C++的代码实现：

  pot P={-inf,-inf},Q={-inf,-inf},R={-inf,-inf};
    n=read();
    for(int i=;i<=n;i++)
    {
        a[i].x=read();a[i].y=read();
        if(dcmp(a[i].y-P.y)==&&dcmp(a[i].x-P.x)<)P=a[i];
        if(dcmp(a[i].y-P.y)>)P=a[i];
        if(i!=)f[++cnt]=a[i]-a[i-];if(i==n)f[++cnt]=a[]-a[i];
    }
    n=read();
    for(int i=;i<=n;i++)
    {
        b[i].x=read();b[i].y=read();
        if(dcmp(b[i].y-Q.y)==&&dcmp(b[i].x-Q.x)<)Q=b[i];
        if(dcmp(b[i].y-Q.y)>)Q=b[i];
        if(i!=)f[++cnt]=b[i]-b[i-];if(i==n)f[++cnt]=b[]-b[i];
    }
    n=read();
    for(int i=;i<=n;i++)
    {
        c[i].x=read();c[i].y=read();
        if(dcmp(c[i].y-R.y)==&&dcmp(c[i].x-R.x)<)R=c[i];
        if(dcmp(c[i].y-R.y)>)R=c[i];
        if(i!=)f[++cnt]=c[i]-c[i-];if(i==n)f[++cnt]=c[]-c[i];
    }
    sort(f+,f+cnt+,cmp);
    pot k=P+Q+R;p[++tot]=k;
    for(int i=;i<=cnt;i++)
    {
        k=k+f[i];
        if(i!=cnt&&dcmp(f[i].x*f[i+].y-f[i].y*f[i+].x)==)continue;
        p[++tot]=k;
    }
    tot--;
k=p[];