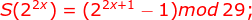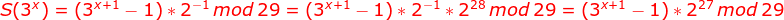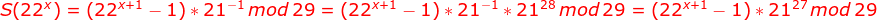HDU 1452 Happy 2004(因数和+费马小定理+积性函数)
Happy 2004
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2183 Accepted Submission(s): 1582
Problem Description
Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your job is to determine S modulo 29 (the rest of the division of S by 29).
Take X = 1 for an example. The positive integer divisors of 2004^1 are 1, 2, 3, 4, 6, 12, 167, 334, 501, 668, 1002 and 2004. Therefore S = 4704 and S modulo 29 is equal to 6.
Input
The input consists of several test cases. Each test case contains a line with the integer X (1 <= X <= 10000000).
A test case of X = 0 indicates the end of input, and should not be processed.
Output
For each test case, in a separate line, please output the result of S modulo 29.
Sample Input
1
10000
0
Sample Output
6
10
Source
ACM暑期集训队练习赛(六)
Recommend
lcy | We have carefully selected several similar problems for you: 1695 1788 1060 1370 1211
题解:
1.积性函数:函数f如果满足对于任意两个互质的正整数m和n,均有f(mn)=f(m)f(n),就称f为积性函数(或乘性函数)。如果对于任意两个正整数m和n,均有f(mn)=f(m)f(n),就称为完全积性函数。
2.因数和函数:
3.因数和函数为积性函数,结合费马小定理:
#include<iostream>
using namespace std;
int mul(int a,int x){
int ans=1;
while(x){
if(x&1)
ans=a*ans%29;
x>>=1;
a=a*a%29;
}
return ans;
}
int main()
{
int x;
while(~scanf("%d",&x)&&x)
{
int ans1=(mul(2,2*x+1)-1)%29;
int ans2=(mul(3,x+1)-1)%29*mul(2,27)%29;
int ans3=(mul(22,x+1)-1)%29*mul(21,27)%29;
printf("%d\n",ans1*ans2*ans3%29);
}
return 0;
}
HDU 1452 Happy 2004(因数和+费马小定理+积性函数)的更多相关文章
- HDU 5667 Sequence 矩阵快速幂+费马小定理
题目不难懂.式子是一个递推式,并且不难发现f[n]都是a的整数次幂.(f[1]=a0;f[2]=ab;f[3]=ab*f[2]c*f[1]...) 我们先只看指数部分,设h[n]. 则 h[1]=0; ...
- 2014多校第一场 I 题 || HDU 4869 Turn the pokers(费马小定理+快速幂模)
题目链接 题意 : m张牌,可以翻n次,每次翻xi张牌,问最后能得到多少种形态. 思路 :0定义为反面,1定义为正面,(一开始都是反), 对于每次翻牌操作,我们定义两个边界lb,rb,代表每次中1最少 ...
- hdu 4869 Turn the pokers(组合数+费马小定理)
Problem Description During summer vacation,Alice stay at home for a long time, with nothing to do. S ...
- HDU——5667Sequence(矩阵快速幂+费马小定理应用)
Sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total S ...
- HDU 4704 Sum (高精度+快速幂+费马小定理+二项式定理)
Sum Time Limit:1000MS Memory Limit:131072KB 64bit IO Format:%I64d & %I64u Submit Status ...
- 数学--数论--HDU 1098 Ignatius's puzzle (费马小定理+打表)
Ignatius's puzzle Problem Description Ignatius is poor at math,he falls across a puzzle problem,so h ...
- 数论初步(费马小定理) - Happy 2004
Description Consider a positive integer X,and let S be the sum of all positive integer divisors of 2 ...
- 数论 --- 费马小定理 + 快速幂 HDU 4704 Sum
Sum Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=4704 Mean: 给定一个大整数N,求1到N中每个数的因式分解个数的 ...
- HDU 4704 Sum(隔板原理+组合数求和公式+费马小定理+快速幂)
题目传送:http://acm.hdu.edu.cn/showproblem.php?pid=4704 Problem Description Sample Input 2 Sample Outp ...
随机推荐
- JS调用函数时候加括号与只写函数名字的区别 fn与fn()的区别
经常见插件里面函数调用的时候只写个函数名字,不写函数参数,甚至连括号也不写,比如说: <!DOCTYPE html> <html> <head> <meta ...
- android动态设置组件LayoutParams
开发中经常用到动态设置组件的LayoutParams,之前开发遇到的问题如下: LinearLayout.LayoutParams params = new LinearLayout.LayoutPa ...
- 鼠标事件event和坐标
鼠标事件(e=e||window.event) event.clientX.event.clientY 鼠标相对于浏览器窗口可视区域的X,Y坐标(窗口坐标),可视区域不包括工具栏和滚动条.IE事件和标 ...
- 1、git基础介绍及远程/本地仓库、分支
1. Git基础介绍 基于Git进行开发时,首先需要将远程仓库代码clone到本地,即为本地仓库.后续大部分时间都是基于本地仓库上的分支进行编码,最后将本地仓库的代码合入远程仓库. 1.1. 远程仓库 ...
- Mudo C++网络库第三章学习笔记
多线程服务器的适用场合与常用编程模型 进程间通信与线程同步; 以最简单规范的方式开发功能正确.线程安全的多线程程序; 多线程服务器是指运行在linux操作系统上的独占式网络应用程序; 不考虑分布式存储 ...
- mybatis:延迟加载时不要在get/set方法上面添加final关键字(原创)
1.mybatis-config.xml: <?xml version="1.0" encoding="UTF-8"?> <!DOCTYPE ...
- kerberos简单介绍
重要术语 1. KDC 全称:key distributed center 作用:整个安全认证过程的票据生成管理服务,其中包含两个服务,AS和TGS 2. AS 全称:authentication s ...
- 【原创】大数据基础之Kerberos(1)简介、安装、使用
kerberos5-1.17 官方:https://kerberos.org/ 一 简介 The Kerberos protocol is designed to provide reliable a ...
- 如何用Axure快速制作APP交互原型
对于产品经理来说,熟练使用一些常用软件是一项十分必要的技能.其中,作为一个专业的快速原型设计工具,Axure RP无疑在产品人心中拥有一个难以撼动的地位.但就要PS一样,虽然足够专业,但同样也会存在使 ...
- 初学python之路-day14
一.带参装饰器 # 通常,装饰器为被装饰的函数添加新功能,需要外界的参数 # -- outer参数固定一个,就是func # -- inner参数固定同被装饰的函数,也不能添加新参数 # -- 可以借 ...