JAVA二分搜索树

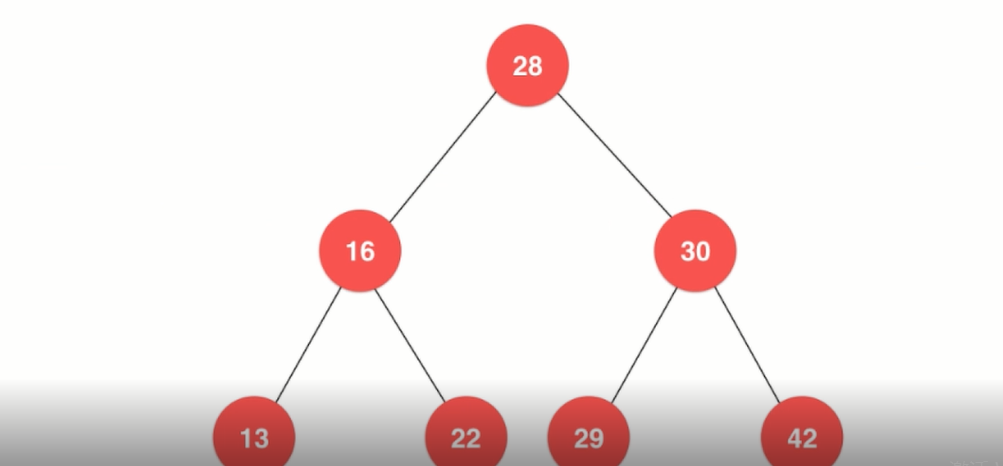
二叉树：

和链表一样，动态数据结构。

二叉树具有唯一根节点

二叉树具有天然的递归结构

二分搜索树是二叉树

二分搜索树的每个节点的值：

1.大于其左子树的所有节点的值

2.小于其右子树的所有节点的值

每一颗子数也是二分搜索树

public class BST<E extends Comparable<E>> {
	private class Node{
		public E e;
		public Node left,right;
		public Node(E e){
			this.e=e;
			left=null;
			right=null;
		}
	}
	private Node root;
	private int size;
	public BST(){
		root=null;
		size=0;
	}
	public int size(){
		return size;
	}
	public boolean isEmpty(){
		return size==0;
	}
 
	public void add(E e){
		if(root==null){
			root=new Node(e);
			size++;
		}else{
			add(root,e);
		}
	}
	向以Node为跟节点的二分搜索树中插入元素E递归算法
	private void add(Node node,E e){
		if(e.equals(node.e)) return ;
		else if(e.compareTo(node.e)<0&&node.left==null){
			node.left=new Node(e);
		    size++;
		    return ;
		}else if(e.compareTo(node.e)>0&&node.right==null){
			node.right=new Node(e);
			size++;
			return;
	}
	if(e.compareTo(node.e)<0)
		add(node.left,e);
	else
		add(node.right, e);
 
public void add(E e){
		root=add(root, e);
	}
	private Node add(Node node,E e){
		if(node==null){
			size++;
			return new Node(e);
		}
		if(e.compareTo(node.e)<0)
			node.left=add(node.left, e);
		else if(e.compareTo(node.e)>0)
			node.right=add(node.right, e);
		return node;
	}
	//看二分搜索树中是否包含元素e
	public boolean contains(E e){
		return contains(root,e)
	}
	//以node为根的二分搜索树中是否包含元素e，递归算法
	public boolean contains(Node node,E e){
		if(node==null)
			return false;
		if(e.compareTo(node.e)==0)
			return true;
		else if(e.compareTo(node.e)<0)
			return contains(node.left,e);
		else
			return contains(node.right, e);
	}
 
}

　　二分搜索树的前序遍历：

//二分搜索树的前序遍历
	public void preOrder(){
		preOrder(root);
	}
	//前序遍历以node为根的二分搜索树，递归算法
	private void preOrder(Node node){
		if(node==null)
			return;
		System.out.println(node.e);
		preOrder(node.left);
		preOrder(node.right);
	}
 
	@Override
	public String toString(){
		StringBuilder res=new StringBuilder();
		generateBSTString(root,0,res);
	    return res.toString();
	}
	//生成node为根节点，深度为depth的描述二叉树的字符串
	private void generateBSTString(Node node,int dept,StringBuilder res){
		if(node==null){
			res.append(generateDepthString(dept)+"null\n");
			return;
		}
		res.append(generateDepthString(dept)+node.e+"\n");
		generateBSTString(node.left,dept+1,res);
		generateBSTString(node.right,dept+1,res);
	}
	private String generateDepthString(int dept) {
		StringBuilder res=new StringBuilder();
		for(int i=0;i<dept;i++)
			res.append("--");
		return res.toString();
	}

　　测试：

public class Main {
     public static void main(String[] args){
    	 BST<Integer> bst=new BST<>();
    	 int[] nums={5,3,6,8,4,2};
    	 for(int num:nums)
    		 bst.add(num);
    	 bst.preOrder();
    	 System.out.println();
    	 System.out.println(bst);
     }
}

　　二分搜索树的中序遍历和后续遍历

//二分搜索树的中序遍历
	public void inOrder(){
		inOrder(root);
	}
	//中序遍历以node为根的二分搜索树，递归算法
	private void inOrder(Node node){
		if(node==null)
			return ;
		inOrder(node.left);
		System.out.println(node.e);
		inOrder(node.right);
	}
	//二分搜索树的后续遍历
	public void postOrder(){
		postOrder(root);
	}
	//后续遍历以node为根的二分搜索树，递归算法
	private void postOrder(Node node){
		if(node==null)
			return ;
		postOrder(node.left);
		postOrder(node.right);
 
		System.out.println(node.e);
	}

　　测试：

bst.preOrder();
    	 System.out.println();
    	 bst.inOrder();
    	 System.out.println();
    	 bst.postOrder();
    	 System.out.println();

　　

//二分搜索树的非递归前序遍历
	public void preOrderNR(){
		Stack<Node> stack=new Stack<>();
		stack.push(root);
		while (!stack.isEmpty()) {
		      Node cur=stack.pop();
		      System.out.println(cur.e);
		      if(cur.right!=null)
		          stack.push(cur.right);
		      if(cur.left!=null)
		          stack.push(cur.left);
		}
	}

	//二分搜索树的层序遍历
	public void levelOrder(){
		Queue<Node> queue=new LinkedList<>();
		queue.add(root);
		while (!queue.isEmpty()) {
             Node cur=queue.remove();
             System.out.println(cur.e);
             if(cur.left!=null)
            	 queue.add(cur.left);
             if(cur.right!=null)
            	 queue.add(cur.right);
		}
	}

　　

//寻找二分搜索树的最小元素
	public E mininum(){
		if(size==0)
             throw new IllegalArgumentException("BST is empty");
		 return mininum(root).e;
	}
	//返回以node为根的二分搜索树的最小值所在的节点
	private Node mininum(Node node){
		if(node.left==null)
			return node;
		return mininum(node.left);
	}
	//寻找二分搜索树的最大元素
	public E maximum(){
		if(size==0)
			throw new IllegalArgumentException("BST is empty");
		return maximum(root).e;
	}
	//返回node为根的二分搜索树的最大值所在的节点
	private Node maximum(Node node){
		if(node.right==null)
			return node;
		return maximum(node.right);
	}
 
	//从二分搜索树中删除最小值所在节点，并返回最小值
	public E removeMin(){
		E ret=mininum();
		root=removeMin(root);
		return ret;
	}
	//删除掉以node为根的二分搜索树中的最小节点
	//返回删除节点后新的二分搜索树的根
	private Node removeMin(Node node){
		if(node.left==null){
			Node rightNode=node.right;
			node.right=null;
			size--;
			return rightNode;
		}
		node.left= removeMin(node.left);
		return node;
	}
 
	//从二分搜索树中删除最大值所在节点
	public E removeMax(){
		E ret=maximum();
		root=removeMax(root);
		return ret;
	}
	//删除掉以node为根的二分搜索树中的最大节点
	//返回删除节点后新的二分搜索树的根
	public Node removeMax(Node node){
		if(node.right==null){
			Node leftNode=node.left;
			node.left=null;
			size--;
			return leftNode;
		}
		node.right=removeMax(node.right);
		return node;
	}

　　测试

public class Main {
     public static void main(String[] args){
    	 BST<Integer> bst=new BST<>();
    	 Random random=new Random();
    	 int n=1000;
    	 for(int i=0;i<n;i++)
    		 bst.add(random.nextInt(10000));
    	 ArrayList<Integer> nums=new ArrayList<>();
    	 while(!bst.isEmpty())
    		 nums.add(bst.removeMin());
    	 System.out.println(nums);
 
    	 for(int i=1;i<nums.size();i++)
    		 if(nums.get(i-1)>nums.get(i))
    			 throw new IllegalArgumentException("Error");
    	 System.out.println("removeMin test completed.");
 
    	 //test removeMax
    	 for(int i=0;i<n;i++)
    		 bst.add(random.nextInt(10000));
    	 nums=new ArrayList<>();
    	 while(!bst.isEmpty())
    		 nums.add(bst.removeMax());
    	 System.out.println(nums);
 
    	 for(int i=1;i<nums.size();i++)
    		 if(nums.get(i-1)<nums.get(i))
    			 throw new IllegalArgumentException("Error");
    	 System.out.println("removeMax test completed.");
 
     }
}

　　

//从二分搜索树中删除元素为e的节点
	public void remove(E e){
	   root=remove(root,e);
	}
	//删除以node为根的二分搜索树中值为e的节点，递归算法
	//返回删除节点后新的二分搜索树的根
	private Node remove(Node node,E e){
		if(node==null)
			return null;
		if(e.compareTo(node.e)<0){
			node.left=remove(node.left, e);
			return node;
		}
		else if(e.compareTo(node.e)>0){
		   node.right=	remove(node.right, e);
		   return node;
		}else {
			//待删除节点左子树为空的情况
			if(node.left==null){
				Node rightNode=node.right;
				node.right=null;
				size--;
				return rightNode;
			}
			//待删除节点右子数为空的情况
			if(node.right==null){
				Node leftNode=node.left;
				node.left=null;
				size--;
				return leftNode;
			}
			//待删除节点左右子数均不为空的情况
			//找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
			//用这个节点顶替待删除节点的位置
			Node successor=mininum(node.right);
			successor.right=removeMin(node.right);
 
			successor.left=node.left;
 
			node.left=node.right=null;
			return successor;
		}
	}