Leetcode | N-Queens I & II

N-Queens I

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

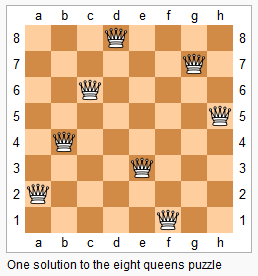
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Wiki：任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当 n = 1 或 n ≥ 4 时问题有解。

回溯，用了一个数组col[i]来表示第i列是不是已经放了queen。

对于(row1, col1)和(row2, col2)这两个位置，如果它们在同一对角线上，那么有abs(row1-row2) = abs(col1-col2)。

class Solution {
public:
    vector<vector<string> > solveNQueens(int n) {
        if (n ==  || n == ) {
            return ret;
        }
        vector<string> sol(n, string(n, '.'));
        vector<bool> col(n, false);
        bt(n, , col, sol);
        return ret;
    }

    void bt(int n, int r, vector<bool> &col, vector<string> &sol) {
        if (r >= n) {
            ret.push_back(sol);
            return;
        }

        for (int i = ; i < n; ++i) {
            if (col[i]) continue;

            bool diag = false;
            for (int j = r - ; j >= ; --j) {
                for (int m = ; m < n; ++m) {
                    if (abs(j - r) == abs(m - i) && sol[j][m] == 'Q') {
                        diag = true;
                        break;
                    }
                }
            }   

            if (!diag) {
                col[i] = true;
                sol[r][i] = 'Q';
                bt(n, r + , col, sol);
                col[i] = false;
                sol[r][i] = '.';
            }
        }

    }

private:
    vector<vector<string> >  ret;
};

N-Queens II

Follow up for N-Queens problem.

Now, instead outputting board configurations, return the total number of distinct solutions.

和N-Queens I 类似，同样需要回溯。

前面回溯的时候需要用到一个额外的数组col[i]，而且用到了sol这个数组来判断对角线元素。

网上的解决方案更巧妙些，用到一个数组sol[i]，存的是第i行可解的列号。

当处理到第r行时，检查前r-1行，看sol[0...r-1]有没有等于i的，有就代表了该列已经有queen了。然后再检查对角线上的。

 class Solution {
 public:
     int totalNQueens(int n) {
         if (n ==  || n == ) {
             return ;
         }
         vector<int> sol(n, -);
         total = ;
         bt(n, , sol);
         return total;
     }

     void bt(int n, int r, vector<int> &sol) {
         if (r >= n) {
             total++;
             return;
         }

         for (int i = ; i < n; ++i) {
             bool valid = true;
             for (int j = r - ; j >= ; --j) {
                 for (int m = ; m < n; ++m) {
                     if (sol[j] == i || abs(j - r) == abs(sol[j] - i)) {
                         valid = false;
                         break;
                     }
                 }
             }   

             if (valid) {
                 int t = sol[r];
                 sol[r] = i;
                 bt(n, r + , sol);
                 sol[r] = t;
             }
         }

     }

 private:
     int total;
 };

第三次写，在返回值统计。至此leetcode三遍刷完。

 class Solution {
 public:
     int totalNQueens(int n) {
         if (n <= ) return ;
         vector<int> colSetted(n, -);
         return recurse(n, , colSetted);
     }

     int recurse(int n, int row, vector<int> &colSetted) {
         if (row >= n) {
             return ;
         }

         int count = ;
         for (int i = ; i < n; ++i) {
             if (colSetted[i] == -) {
                 bool couldSet = true;
                 for (int j = ; j < n; ++j) {
                     if (colSetted[j] != - && abs(row - colSetted[j]) == abs(i - j)) {
                         couldSet = false;
                         break;
                     }
                 }
                 if (couldSet) {
                     colSetted[i] = row;
                     count += recurse(n, row + , colSetted);
                     colSetted[i] = -;
                 }
             }
         }
         return count;
     }
 };