POJ 2699 The Maximum Number of Strong Kings Description

The Maximum Number of Strong Kings

 

Description

A tournament can be represented by a complete graph in which each vertex denotes a player and a directed edge is from vertex x to vertex y if player x beats player y. For a player x in a tournament T, the score of x is the number of players beaten by x. The score sequence of T, denoted by S(T) = (s1, s2, . . . , sn), is a non-decreasing list of the scores of all the players in T. It can be proved that S(T) = (s1, s2, . . . , sn) is a score sequence of T if and only if 
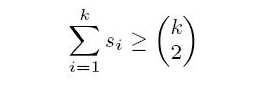
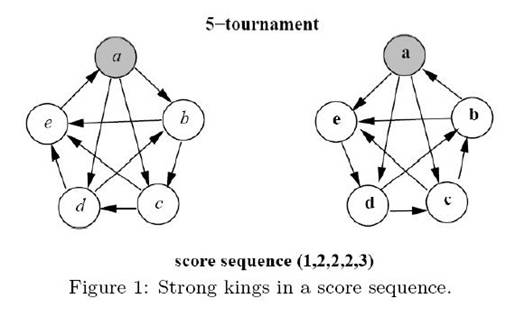
for k = 1, 2, . . . , n and equality holds when k = n. A player x in a tournament is a strong king if and only if x beats all of the players whose scores are greater than the score of x. For a score sequence S, we say that a tournament T realizes S if S(T) = S. In particular, T is a heavy tournament realizing S if T has the maximum number of strong kings among all tournaments realizing S. For example, see T2 in Figure 1. Player a is a strong king since the score of player a is the largest score in the tournament. Player b is also a strong king since player b beats player a who is the only player having a score larger than player b. However, players c, d and e are not strong kings since they do not beat all of the players having larger scores. 
The purpose of this problem is to find the maximum number of strong kings in a heavy tournament after a score sequence is given. For example,Figure 1 depicts two possible tournaments on five players with the same score sequence (1, 2, 2, 2, 3). We can see that there are at most two strong kings in any tournament with the score sequence (1, 2, 2, 2, 3) since the player with score 3 can be beaten by only one other player. We can also see that T2 contains two strong kings a and b. Thus, T2 is one of heavy tournaments. However, T1 is not a heavy tournament since there is only one strong king in T1. Therefore, the answer of this example is 2. 

Input

The first line of the input file contains an integer m, m <= 10, which represents the number of test cases. The following m lines contain m score sequences in which each line contains a score sequence. Note that each score sequence contains at most ten scores.

Output

The maximum number of strong kings for each test case line by line.

Sample Input

5
1 2 2 2 3
1 1 3 4 4 4 4
3 3 4 4 4 4 5 6 6 6
0 3 4 4 4 5 5 5 6
0 3 3 3 3 3

Sample Output

2
4
5
3
5

#include<cstdio>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
const int MAXN=;
int s[],id[][],v[][],cnt1,cnt2;
char str[];
struct dinic
{
    struct Edge
    {
        int from,to,cap,flow;
        Edge(){}
        Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){};
    };
    int s,t,d[MAXN],cur[MAXN];
    bool vis[MAXN];
    vector<Edge>edges;
    vector<int>G[MAXN];
    inline void init()
    {
        for(int i=;i<;i++)G[i].clear();
        edges.clear();
    }
    void addedge(int from,int to,int cap)
    {
        edges.push_back((Edge){from,to,cap,});
        edges.push_back((Edge){to,from,,});
        int m=edges.size();
        G[from].push_back(m-);
        G[to].push_back(m-);
    }
    bool bfs()
    {
        memset(vis,,sizeof(vis));
        queue<int>q;
        q.push(s);
        d[s]=;
        vis[s]=;
        while(!q.empty())
        {
            int x=q.front();q.pop();
            for(int i=;i<G[x].size();i++)
            {
                Edge& e=edges[G[x][i]];
                if(!vis[e.to]&&e.cap>e.flow)
                {
                    vis[e.to]=;
                    d[e.to]=d[x]+;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int dfs(int x,int a)
    {
        if(x==t||a==)return a;
        int flow=,f;
        for(int& i=cur[x];i<G[x].size();i++)
        {
            Edge& e=edges[G[x][i]];
            if(d[x]+==d[e.to]&&(f=dfs(e.to,min(a,e.cap-e.flow)))>)
            {
                e.flow+=f;
                edges[G[x][i]^].flow-=f;
                flow+=f;
                a-=f;
                if(a==)break;
            }
        }
        return flow;
    }
    int maxflow(int s,int t)
    {
        this->s=s,this->t=t;
        int flow=;
        while(bfs())
        {
            memset(cur,,sizeof(cur));
            flow+=dfs(s,2e5+);
        }
        return flow;
    }
}dc;
bool check(int x)
{
    dc.init();
    memset(v,,sizeof(v));
    for(int i=;i<=cnt1;i++)
        dc.addedge(,i,s[i]);
    for(int i=;i<=x;i++)
        for(int j=i+;j<=x;j++)
            if(s[i]>s[j])
                dc.addedge(j,id[i][j],),v[i][j]=;
    for(int i=;i<=cnt1;i++)
        for(int j=i+;j<=cnt1;j++)
        {
            dc.addedge(id[i][j],cnt1+cnt2+,);
            if(!v[i][j])
                dc.addedge(i,id[i][j],),dc.addedge(j,id[i][j],);
        }
    return dc.maxflow(,cnt1+cnt2+)==cnt1*(cnt1-)/;
}
int main()
{
    int T;
    scanf("%d",&T);
    getchar();
    while(T--)
    {
        gets(str);
        cnt1=cnt2=;
        for(int i=,len=strlen(str);i<len;i++)
            if(str[i]!=' ')
                s[++cnt1]=(int)str[i]-'';
        for(int i=;i<=cnt1/;i++)
            swap(s[i],s[cnt1-i+]);
        for(int i=;i<=cnt1;i++)
            for(int j=i+;j<=cnt1;j++)
                id[i][j]=++cnt2+cnt1;
        for(int i=cnt1;i>=;i--)
            if(check(i))
            {
                printf("%d\n",i);
                break;
            }
    }
    return ;
}