Largest Rectangle in a Histogram

2107: Largest Rectangle in a Histogram

Time Limit: 1 Sec  Memory Limit: 64 MB
Submit: 777  Solved: 220

Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

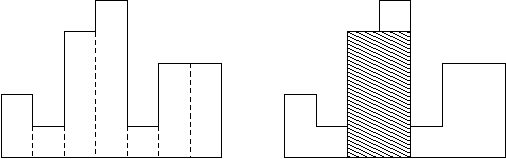
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1<=n<=100000. Then follow n integers h₁,...,h_n, where 0<=h_i<=1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

HINT

Huge input, scanf is recommended.

如果确定了长方形的左端点L和右端点R，那么最大可能的高度就是min{hi|L <= i < R}。

L[i] = (j <= i并且h[j-1] < h[i]的最大的j)

R[i] = (j > i并且h[j] > h[i]的最小的j)

 #include <stdio.h>
 #define MAX_N 100000

 int n;
 int h[MAX_N];
 int L[MAX_N], R[MAX_N];
 int stack[MAX_N];

 long long max(long long a, long long b)
 {
     return (a > b) ? a : b;
 }

 void solve()
 {
     //计算L
     long long ans = ;
     int t = ;
     int i;
     for (i = ; i < n; ++i)
     {
         while (t >  && h[stack[t-]] >= h[i])
             t--;
         L[i] = (t == ) ?  : (stack[t-] + );
         stack[t++] = i;
     }

     //计算R
     t = ;
     for (i = n - ; i >= ; --i)
     {
         while (t >  && h[stack[t-]] >= h[i])
             t--;
         R[i] = (t == ) ? n : stack[t-];
         stack[t++] = i;
     }

     for (i = ; i < n; ++i)
     {
         ans=max ( ans, ( long long)h[i]*( R[i]- L[i]));
     }
     printf("%lld\n", ans);
 }

 int main(void){
    // freopen("a.txt","r",stdin);
     int i;
     while (scanf("%d", &n) != EOF && n != )
     {
         for (i = ; i < n; ++i)
             scanf("%d", &h[i]);
         solve();
     }

     return ;
 }

Acknowledge:jdplus     http://blog.csdn.net/jdplus/article/details/20606673