Floyd-Warshall算法

　　Floyd也是采用动态规划的方案来解决在一个有向图G=（V，E）上每对顶点间的最短路径问题。运行时间为Θ（V³）。

算法分析：

　　用邻接矩阵map[][]存储有向图，用dist[i][j]表示i到j的最短路径。设G的顶点为V={1,2,3...n}，对于任意一对顶点i,j属于V，假设i到j有路径且中间节点皆属于集合{1,2,3...k}，P是其中的一条最小权值路径。就是i到j的最短路径P所通过的中间顶点最大不超过k。

　　设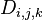为从到的只以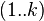集合中的节点为中间节点的最短路径的长度。

1. 若最短路径经过点k，则；
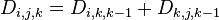2. 若最短路径不经过点k，则。

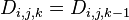　　因此，。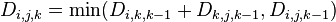

for k ←  to n do
  for i ←  to n do
    for j ←  to n do
      if (Di,k + Dk,j < Di,j) then
         Di,j←Di,k + Dk,j ;

实现代码：

/*************************************************************************
    > File Name: Floyd_Warshall.cpp
    > Author: He Xingjie
    > Mail: gxmshxj@163.com
    > Created Time: 2014年06月12日 星期四 15时57分22秒
    > Description:
 ************************************************************************/
#include<iostream>
#include<cstdio>
using namespace std;

#define MAX 20
#define INF 65535

//map邻接矩阵，dist记录最短路径,path用于最短路径
int map[MAX][MAX], dist[MAX][MAX], path[MAX][MAX];

int Init()
{
    int n;

    cin>>n;
    for (int i=; i<n; i++)
        for(int j=; j<n; j++)
        {
            cin>>map[i][j];
            dist[i][j] = map[i][j];
            path[i][j] = ;
        }

    return n;
}

void Floyd(int n)
{
    int i, j, k;

    for (k=; k<n; k++)
        for (i=; i<n; i++)
            for (j=; j<n; j++)
                if (dist[i][k] != INF && dist[k][j] !=INF
                        && dist[i][j] > dist[i][k] + dist[k][j])
                {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    path[i][j] = k;        //i到j要经过K节点
                }
}

void PrintShortestPath(int i, int j)
{
    //递归打印最短路径

    if (path[i][j] == )    //表示i->j没有中间节点
    {
        printf("%d ", j+);
        return;
    }
    else
    {
        PrintShortestPath(i, path[i][j]);
        PrintShortestPath(path[i][j], j);
    }
}

void PrintMap(int n)
{
    int i, j;

    for    (i=; i<n; i++)
    {
        for (j=; j<n; j++)
            cout<<dist[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}

int main()
{
    int n;

    freopen("input.txt", "r", stdin);
    n = Init();
    Floyd(n);
    PrintMap(n);

    for (int i=; i<n; i++)
    {
        for (int j=; j<n; j++)
        {
            if (i != j)
            {
                cout<<i+<<" ";
                PrintShortestPath(i, j);
                cout<<endl;
            }
        }
        cout<<endl;
    }
    return ;
}

//  ：

 输入数据：

    -

  -
    

输出数据：

参考：

http://zh.wikipedia.org/zh/%E5%BC%97%E6%B4%9B%E4%BC%8A%E5%BE%B7%E7%AE%97%E6%B3%95

http://www.cppblog.com/mythit/archive/2009/04/21/80579.aspx