离散傅立叶变换与快速傅立叶变换（DFT与FFT）

自从去年下半年接触三维重构以来，听得最多的词就是傅立叶变换，后来了解到这个变换在图像处理里面也是重点中的重点。

本身自己基于高数知识的理解是傅立叶变换是将一个函数变为一堆正余弦函数的和的变换。而图像处理里则强调它是将图像信息从空间域往频率域转化的重要手段。最近从头学起数字图像处理，看完傅立叶变换之后，对于其中的计算方法快速傅立叶变换产生了好奇。于是搜索了下FFT，发现杭电上有几个这样的题目，其中点击率最高的是hdu1402*大数乘法。

大数乘法本来是一个n方的算法，经过FFT之后可以变为nlogn，于是看了下算法导论中多项式与FFT一节，大致弄清楚了FFT的原理和简单实现。

1.多项式的两种表示：系数表示和点对表示，两种表示之间可以互相转化，一个叫做赋值，一个叫做插值，插值是一个解带有克里蒙德行列式的过程。

2.为了让多项式乘法更快进行，可以选取一些特殊的数值作为赋值，这些特殊数值就是单位复根。

3.单位复根有相消引理和折半引理，这些可以使赋值以及插值的时间复杂度降低

4.以某个单位复根代入多项式得到的表达式就是离散傅立叶变换。（向量->数值）

5.继续分析多项式表示，可以引出一个蝴蝶操作，以及利用一个二进制平摊反转置换的预处理，使FFT可以迭代进行。

6.同时逆FFT可以采用和FFT相同的方式实现。

7.大数乘法可以看成两个多项式相乘，然后令变量为10的结果。

自学一个新的算法其实最容易的入门方式就是找一组数据试一试，在计算（1,2,3,4）的离散傅里叶变换之后自己就更清楚为什么蝴蝶操作是可以进行的。

假设两个4321相乘，那么n扩展为8

1.fft数组初始化就是（1,2,3,4,0,0,0,0）。而目的是求出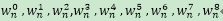（）这个对应的值

2.以wn0为例：

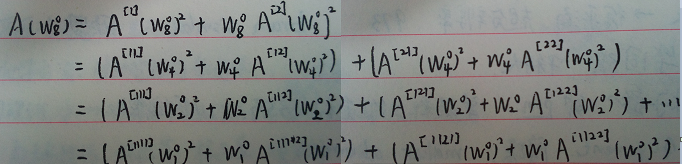
系数形成的树如下：

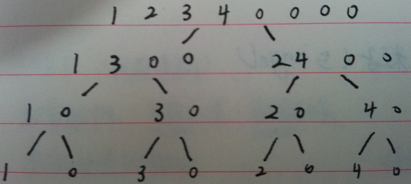
第一次进行n=2的傅里叶变换之后，系数如下：

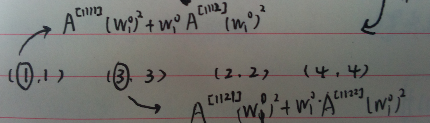
第二次进行n=4的傅里叶变换之后，系数如下：

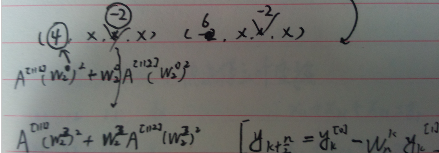
而在这步变化里同时体现了蝶形操作：（k）与（k+n/2的关系）

hdu1402:---代码实现：

#include <iostream>
#include <cmath>
#include <string.h>
using namespace std;
#define N 200005
#define PI acos(-1.0)
struct complex
{
    double r,i;
    complex(double real=0.0,double image=0.0)
    {
        r=real;
        i=image;
    }
    //以下为三种虚数运算的定义
    complex operator+(const complex o)
    {
        return complex(r+o.r,i+o.i);
    }
    complex operator-(const complex o)
    {
        return complex(r-o.r,i-o.i);
    }
    complex operator*(const complex o)
    {
        return complex(r*o.r-i*o.i,r*o.i+i*o.r);
    }
}x1[N],x2[N];
char a[N/],b[N/];
int sum[N]; //结果存在sum里   

void bitrev(complex *y,int l) //二进制平摊反转置换 O(logn)
{
    register int i,j,k;
    for(i=,j=l/;i<l-;i++)
    {
        if(i<j)  swap(y[i],y[j]); //交换互为下标反转的元素
                                 //i<j保证只交换一次
        k=l/;
        while(j>=k) //由最高位检索，遇1变0，遇0变1，跳出
        {
            j-=k;
            k/=;
        }
        if(j<k)  j+=k;
    }
}
void fft(complex *in,int n)
{
    int i,j,k;
    complex u,t;
    bitrev(in,n);
    for(int i=;i<=n;i=i*)
    {
        complex wn(cos((*PI)/i),sin((*PI)/i));//初始化单位复根
        for(j=;j<n;j=j+i)
        {
            complex w(,);
            for(k=j;k<j+i/;k++)
            {
                u=in[k];
                t=w*in[k+i/];
                in[k]=u+t;
                in[k+i/]=u-t;
                w=w*wn;
            }
        }
    }
}
void antifft(complex *in,int n)
{
    complex x,y;
    int i,j,k;
    bitrev(in,n);
    for(int i=;i<=n;i=i*)
    {
        complex init(cos((*PI*-)/i),sin((*PI*-)/i));
        for(j=;j<n;j=j+i)
        {
            complex w(,);
            for(k=j;k<j+i/;k++)
            {
                x=in[k];
                y=w*in[k+i/];
                in[k]=x+y;in[k+i/]=x-y;
                w=w*init;
            }
        }
    }
    for(int i=;i<n;i++)
        in[i]=in[i].r/n;
}

int main() {

    while(~scanf("%s%s",a,b))
    {
        //提取系数并逆序
        int na=strlen(a);
        int nb=strlen(b);

        int n=;
        //expand

        while(n<na* || n<nb*)   n=n*; //将次数界变成2^n
        for(int i=na-;i>=;i--)
        {
            x1[na--i].r=a[i]-'';x1[na--i].i=;
        }

        for(int i=nb-;i>=;i--)
        {
            x2[nb--i].r=b[i]-'';x2[nb--i].i=;
        }

        for(int i=na;i<n;i++)
        {
            x1[i].i=;x1[i].r=;
        }
        for(int i=nb;i<n;i++)
        {
            x2[i].i=;x2[i].r=;
        }

        //分别傅里叶变换
        fft(x1,n);
        fft(x2,n);
        //点值相乘得到新的傅里叶变换数值
        for(int i=;i<n;i++)
            x1[i]=x1[i]*x2[i];
        //逆傅里叶变换得到系数，*10求和
        antifft(x1,n);
        memset(sum,,sizeof(sum));
        //四舍五入
        for(int i=;i<n;i++)
            sum[i]=x1[i].r+0.5;
        for(int i=;i<n;i++) //进位
        {
            sum[i+]+=sum[i]/;
            sum[i]%=;
        }
        while(sum[n]<= && n>)   n--; //检索最高位   

        for(int i=n;i>=;i--)
            putchar(sum[i]+''); //倒序输出
        printf("\n");
    }
    return ;

}

代码参照：http://blog.csdn.net/u011328276/article/details/10020723

PS：csdn这份代码没有每次将sum初始化，有时会造成错误结果。

Accepted

1402

375MS

7492K

3484 B

G++