Back Propagation - Python实现

• 算法特征
  ①. 统一看待线性运算与非线性运算; ②. 确定求导变量loss影响链路; ③. loss影响链路梯度逐级反向传播.
• 算法推导
  Part Ⅰ
  以如下简单正向传播链为例, 引入线性运算与非线性运算符号,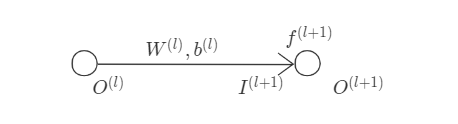
  
  相关运算流程如下,
  $$
  \begin{equation*}
  \begin{split}
  &\text{linear operation } & I^{(l+1)} = W^{(l)}\cdot O^{(l)} + b^{(l)} \\
  &\text{non-linear operation }\quad & O^{(l+1)} = f^{(l+1)}(I^{(l+1)})
  \end{split}
  \end{equation*}
  $$
  其中, $O^{(l)}$、$I^{(l+1)}$、$O^{(l+1)}$分别为第$l$层输出(output)、第$l+1$层输入(input)、第$l+1$层输出, $W^{(l)}$、$b^{(l)}$、$f^{(l+1)}$分别为相关weight、bias及activation function. 对于线性运算, bias可合并至weight, 则
  $$
  \begin{equation*}
  \text{linear operation }\quad I^{(l+1)} = \tilde{W}^{(l)}\cdot \tilde{O}^{(l)} = g^{(l)}(\tilde{O}^{(l)})
  \end{equation*}
  $$
  其中, $\tilde{W}^{(l)} = [W^{(l)\mathrm{T}}, b^{(l)}]^\mathrm{T}$, $\tilde{O}^{(l)}=[O^{(l)\mathrm{T}},1]^\mathrm{T}$.
  对于上述简单正向传播链, 基础影响链路如下,
  
  $$
  \begin{equation*}
  \begin{split}
  &\tilde{O}^{(l)} &\quad\rightarrow\quad I^{(l+1)} \\
  &\tilde{W}^{(l)} &\quad\rightarrow\quad I^{(l+1)} \\
  &I^{(l+1)} &\quad\rightarrow\quad O^{(l+1)}
  \end{split}
  \end{equation*}
  $$
  根据链式法则, 影响链路起点由求导变量决定, 终点位于Loss处.
  Part Ⅱ
  现以如下神经网络为例, 加以阐述,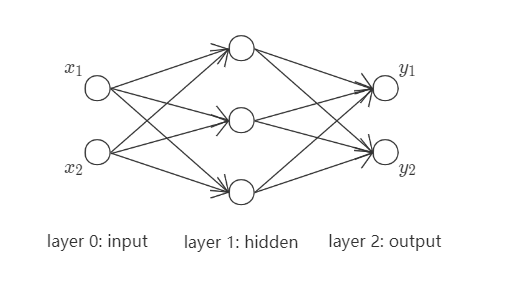
  

  其中, $(x_1, x_2)$为网络输入, $(y_1, y_2)$为网络输出. 统一处理其中线性运算与非线性运算, 并将该网络完全展开,
  

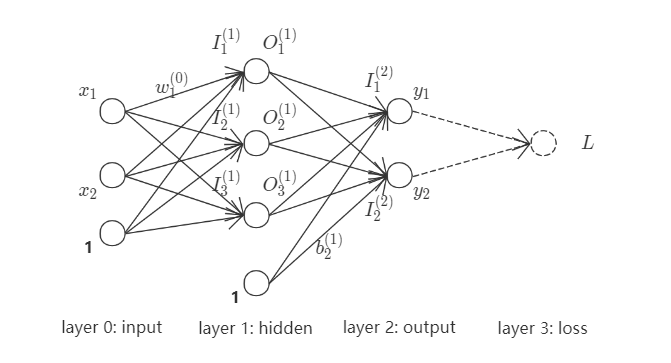
  现以$w_1^{(0)}$为例, 作为求导变量确定loss影响链路. $w_1^{(0)}$之loss影响链路(红色+绿色箭头)如下,
  

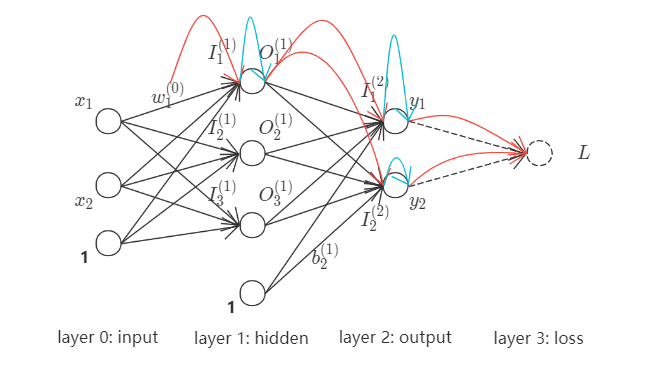
  拆解为基础影响链路, 如下,
  $$
  \begin{equation*}
  \begin{split}
  & w_1^{(0)} &\quad\rightarrow\quad I_1^{(1)} \\
  & I_1^{(1)} &\quad\rightarrow\quad O_1^{(1)} \\
  & O_1^{(1)} &\quad\rightarrow\quad I_1^{(2)} \\
  & O_1^{(1)} &\quad\rightarrow\quad I_2^{(2)} \\
  & I_1^{(2)} &\quad\rightarrow\quad y_1 \\
  & I_2^{(2)} &\quad\rightarrow\quad y_2 \\
  & y_1 &\quad\rightarrow\quad L \\
  & y_2 &\quad\rightarrow\quad L
  \end{split}
  \end{equation*}
  $$
  定义源(source)为存在多个下游分支的节点(如: $O_1^{(1)}$), 定义汇(sink)为存在多个上游分支的节点(如: $L$). 根据链式求导法则, 在影响链路上, 下游变量对源变量求导需要在源变量处求和, 汇变量对上游变量求导无需特殊处理, 即,
  
  $$
  \begin{equation*}
  \begin{split}
  &\text{source variable $x$: }\quad &\frac{\partial J(u(x), v(x))}{\partial x} &= \frac{\partial J(u(x), v(x))}{\partial u}\cdot\frac{\partial u}{\partial x} + \frac{\partial J(u(x), v(x))}{\partial v}\cdot\frac{\partial v}{\partial x} \\
  &\text{sink variable $J$: }\quad &\frac{\partial J(u(x), v(y))}{\partial x} &= \frac{\partial J(u(x), v(y))}{\partial u}\cdot\frac{\partial u}{\partial x}
  \end{split}
  \end{equation*}
  $$
  由此, 根据梯度沿影响链路的反向传播, 可确定loss对$w_1^{(0)}$之偏导,
  
  $$
  \begin{equation*}
  \frac{\partial L}{\partial w_1^{(0)}} = \left(\frac{\partial L}{\partial y_1}\cdot\frac{\partial y_1}{\partial I_1^{(2)}}\cdot\frac{\partial I_1^{(2)}}{\partial O_1^{(1)}} + \frac{\partial L}{\partial y_2}\cdot\frac{\partial y_2}{\partial I_2^{(2)}}\cdot\frac{\partial I_2^{(2)}}{\partial O_1^{(1)}}\right)\cdot\frac{\partial O_1^{(1)}}{\partial I_1^{(1)}}\cdot\frac{\partial I_1^{(1)}}{\partial w_1^{(0)}}
  \end{equation*}
  $$
  再以$b_2^{(1)}$为例, 作为求导变量确定loss影响链路. $b_2^{(1)}$之loss影响链路(红色+绿色箭头)如下,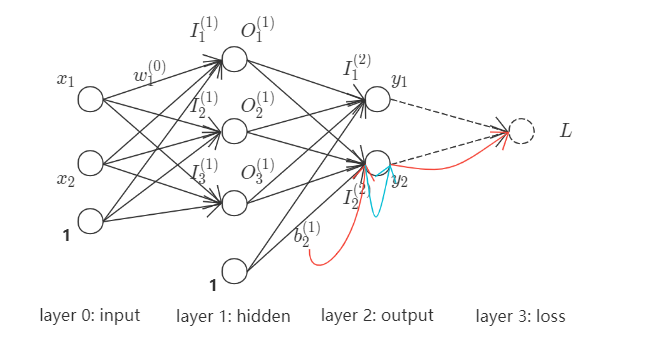
  

  拆解为基础影响链路, 如下,
  $$
  \begin{equation*}
  \begin{split}
  & b_2^{(1)} &\quad\rightarrow\quad I_2^{(2)} \\
  & I_2^{(2)} &\quad\rightarrow\quad y_2 \\
  & y_2 &\quad\rightarrow\quad L
  \end{split}
  \end{equation*}
  $$
  同样, 根据梯度沿影响链的反向传播, 可确定loss对$b_2^{(1)}$之偏导,
  
  $$
  \begin{equation*}
  \frac{\partial L}{\partial b_2^{(1)}} = \frac{\partial L}{\partial y_2}\cdot\frac{\partial y_2}{\partial I_2^{(2)}}\cdot\frac{\partial I_2^{(2)}}{\partial b_2^{(1)}}
  \end{equation*}
  $$

• 代码实现
  现以如下简单feed-forward网络为例进行算法实施,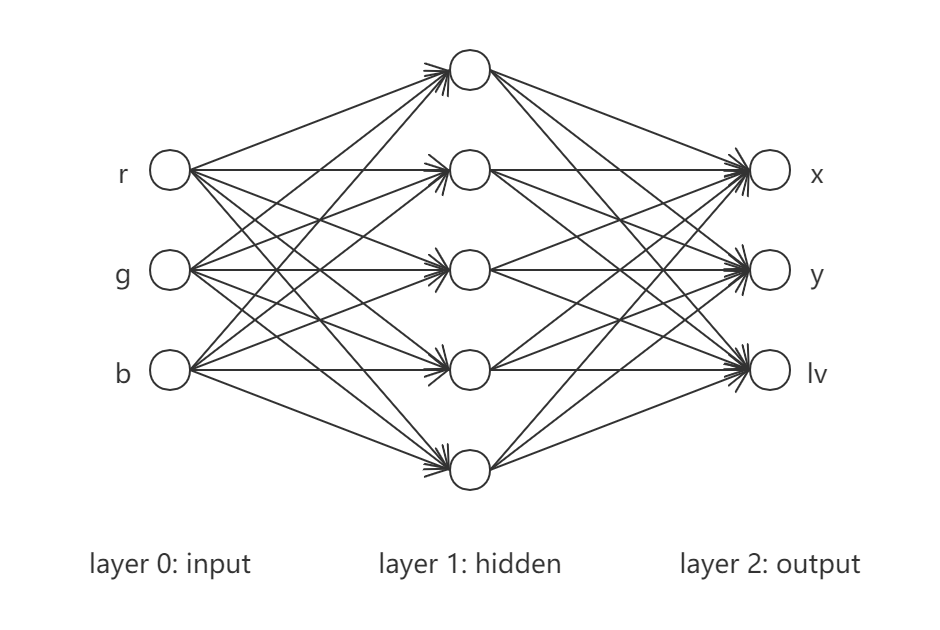
  

  输入层为$(r, g, b)$, 输出层为$(x,y,lv)$且不取激活函数, 中间隐藏层取激活函数为双曲正切函数$\tanh$. 采用如下损失函数,
  $$
  \begin{equation*}
  L = \sum_i\frac{1}{2}(\bar{x}^{(i)}-x^{(i)})^2 + \frac{1}{2}(\bar{y}^{(i)} - y^{(i)})^2 + \frac{1}{2}(\bar{lv}^{(i)} - lv^{(i)})^2
  \end{equation*}
  $$
  其中, $i$为data序号, $(\bar{x}, \bar{y}, \bar{lv})$为相应观测值. 相关training data采用如下策略生成,
  
  $$
  \begin{equation*}
  \left\{
  \begin{split}
  x &= r + 2g + 3b \\
  y &= r^2 + 2g^2 + 3b^2 \\
  lv &= -3r - 4g - 5b
  \end{split}
  \right.
  \end{equation*}
  $$
  具体实现如下,

  

    1 # Back Propagation之实现
    2 # 优化器使用Adam
    3
    4 import numpy
    5 from matplotlib import pyplot as plt
    6
    7
    8 numpy.random.seed(1)
    9
   10
   11 # 生成training data
   12 def getData(n=100):
   13     rgbRange = (-1, 1)
   14     r = numpy.random.uniform(*rgbRange, (n, 1))
   15     g = numpy.random.uniform(*rgbRange, (n, 1))
   16     b = numpy.random.uniform(*rgbRange, (n, 1))
   17     x_ = r + 2 * g + 3 * b
   18     y_ = r ** 2 + 2 * g ** 2 + 3 * b ** 2
   19     lv_ = -3 * r - 4 * g - 5 * b
   20     RGB = numpy.hstack((r, g, b))
   21     XYLv_ = numpy.hstack((x_, y_, lv_))
   22     return RGB, XYLv_
   23
   24
   25 class BPEx(object):
   26
   27     def __init__(self, RGB, XYLv_):
   28         self.__RGB = RGB
   29         self.__XYLv_ = XYLv_
   30
   31         self.__rgb = None           # (1, 3)
   32         self.__O0 = None            # (1, 4)
   33         self.__W0 = None            # (4, 5)
   34         self.__I1 = None            # (1, 5)
   35         self.__O1 = None            # (1, 6)
   36         self.__W1 = None            # (6, 3)
   37         self.__I2 = None            # (1, 3)
   38         self.__xylv_ = None         # (1, 3)
   39         self.__L = None             # scalar
   40
   41         self.__grad_W0_I1 = None    # 基础影响链路(W0->I1)之梯度
   42         self.__grad_I1_O1 = None    # 基础影响链路(I1->O1)之梯度
   43         self.__grad_O1_I2 = None    # 基础影响链路(O1->I2)之梯度
   44         self.__grad_W1_I2 = None    # 基础影响链路(W1->I2)之梯度
   45         self.__grad_I2_L = None     # 基础影响链路(I2->Loss)之梯度
   46
   47         self.__gradList_W0_I1 = list()
   48         self.__gradList_I1_O1 = list()
   49         self.__gradList_O1_I2 = list()
   50         self.__gradList_W1_I2 = list()
   51         self.__gradList_I2_L = list()
   52
   53         self.__init_weights()
   54         self.__bpTag = False        # 是否反向传播之标志
   55
   56
   57     def calc_xylv(self, rgb, W0=None, W1=None):
   58         '''
   59         默认在当前W0、W1之基础上进行预测, 实际使用需要配合优化器
   60         '''
   61         if W0 is not None:
   62             self.__W0 = W0
   63         if W1 is not None:
   64             self.__W1 = W1
   65
   66         self.__calc_xylv(numpy.array(rgb).reshape((1, 3)))
   67         xylv = self.__I2
   68         return xylv
   69
   70
   71     def get_W0W1(self):
   72         return self.__W0, self.__W1
   73
   74
   75     def calc_JVal(self, W):
   76         self.__bpTag = True
   77         self.__clr_gradList()
   78
   79         self.__W0 = W[:20, 0].reshape((4, 5))
   80         self.__W1 = W[20:, 0].reshape((6, 3))
   81
   82         JVal = 0
   83         for rgb, xylv_ in zip(self.__RGB, self.__XYLv_):
   84             self.__calc_xylv(rgb.reshape((1, 3)))
   85             self.__calc_loss(xylv_.reshape((1, 3)))
   86             JVal += self.__L
   87             self.__add_gradList()
   88
   89         self.__bpTag = False
   90         return JVal
   91
   92
   93     def calc_grad(self, W):
   94         '''
   95         此处W仅为统一调用接口
   96         '''
   97         grad_W0 = numpy.zeros(self.__W0.shape)
   98         grad_W1 = numpy.zeros(self.__W1.shape)
   99         for grad_W0_I1, grad_I1_O1, grad_O1_I2, grad_W1_I2, grad_I2_L in zip(self.__gradList_W0_I1,\
  100             self.__gradList_I1_O1, self.__gradList_O1_I2, self.__gradList_W1_I2, self.__gradList_I2_L):
  101             grad_W1_curr = grad_I2_L * grad_W1_I2
  102             grad_W1 += grad_W1_curr
  103
  104             term0 = numpy.sum(grad_I2_L.T * grad_O1_I2, axis=0)   # (1, 5) source
  105             term1 = term0 * grad_I1_O1
  106             grad_W0_curr = term1 * grad_W0_I1
  107             grad_W0 += grad_W0_curr
  108
  109         grad = numpy.vstack((grad_W0.reshape((-1, 1)), grad_W1.reshape((-1, 1))))
  110         return grad
  111
  112
  113     def init_seed(self):
  114         n = self.__W0.size + self.__W1.size
  115         seed = numpy.random.uniform(-1, 1, (n, 1))
  116         return seed
  117
  118
  119     def __add_gradList(self):
  120         self.__gradList_W0_I1.append(self.__grad_W0_I1)
  121         self.__gradList_I1_O1.append(self.__grad_I1_O1)
  122         self.__gradList_O1_I2.append(self.__grad_O1_I2)
  123         self.__gradList_W1_I2.append(self.__grad_W1_I2)
  124         self.__gradList_I2_L.append(self.__grad_I2_L)
  125
  126
  127     def __clr_gradList(self):
  128         self.__gradList_W0_I1.clear()
  129         self.__gradList_I1_O1.clear()
  130         self.__gradList_O1_I2.clear()
  131         self.__gradList_W1_I2.clear()
  132         self.__gradList_I2_L.clear()
  133
  134
  135     def __init_weights(self):
  136         self.__W0 = numpy.zeros((4, 5))
  137         self.__W1 = numpy.zeros((6, 3))
  138
  139
  140     def __update_grad_by_calc_xylv(self):
  141         self.__grad_W0_I1 = numpy.tile(self.__O0.T, (1, 5))
  142         self.__grad_I1_O1 = 1 - self.__I1_tanh ** 2
  143         self.__grad_O1_I2 = self.__W1.T[:, :-1]
  144         self.__grad_W1_I2 = numpy.tile(self.__O1.T, (1, 3))
  145
  146
  147     def __calc_xylv(self, rgb):
  148         '''
  149         rgb: shape=(1, 3)之numpy array
  150         '''
  151         self.__rgb = rgb
  152         self.__O0 = numpy.hstack((self.__rgb, [[1]]))
  153         self.__I1 = numpy.matmul(self.__O0, self.__W0)
  154         self.__I1_tanh = numpy.tanh(self.__I1)
  155         self.__O1 = numpy.hstack((self.__I1_tanh, [[1]]))
  156         self.__I2 = numpy.matmul(self.__O1, self.__W1)
  157
  158         if self.__bpTag:
  159             self.__update_grad_by_calc_xylv()
  160
  161
  162     def __update_grad_by_calc_loss(self):
  163         self.__grad_I2_L = self.__I2 - self.__xylv_
  164
  165
  166     def __calc_loss(self, xylv_):
  167         '''
  168         xylv_: shape=(1, 3)之numpy array
  169         '''
  170         self.__xylv_ = xylv_
  171         self.__L = numpy.sum((self.__xylv_ - self.__I2) ** 2) / 2
  172
  173         if self.__bpTag:
  174             self.__update_grad_by_calc_loss()
  175
  176
  177 class Adam(object):
  178
  179     def __init__(self, _func, _grad, _seed):
  180         '''
  181         _func: 待优化目标函数
  182         _grad: 待优化目标函数之梯度
  183         _seed: 迭代起始点
  184         '''
  185         self.__func = _func
  186         self.__grad = _grad
  187         self.__seed = _seed
  188
  189         self.__xPath = list()
  190         self.__JPath = list()
  191
  192
  193     def get_solu(self, alpha=0.001, beta1=0.9, beta2=0.999, epsilon=1.e-8, zeta=1.e-6, maxIter=3000000):
  194         '''
  195         获取数值解,
  196         alpha: 步长参数
  197         beta1: 一阶矩指数衰减率
  198         beta2: 二阶矩指数衰减率
  199         epsilon: 足够小正数
  200         zeta: 收敛判据
  201         maxIter: 最大迭代次数
  202         '''
  203         self.__init_path()
  204
  205         x = self.__init_x()
  206         JVal = self.__calc_JVal(x)
  207         self.__add_path(x, JVal)
  208         grad = self.__calc_grad(x)
  209         m, v = numpy.zeros(x.shape), numpy.zeros(x.shape)
  210         for k in range(1, maxIter + 1):
  211             print("iterCnt: {:3d},   JVal: {}".format(k, JVal))
  212             if self.__converged1(grad, zeta):
  213                 self.__print_MSG(x, JVal, k)
  214                 return x, JVal, True
  215
  216             m = beta1 * m + (1 - beta1) * grad
  217             v = beta2 * v + (1 - beta2) * grad * grad
  218             m_ = m / (1 - beta1 ** k)
  219             v_ = v / (1 - beta2 ** k)
  220
  221             alpha_ = alpha / (numpy.sqrt(v_) + epsilon)
  222             d = -m_
  223             xNew = x + alpha_ * d
  224             JNew = self.__calc_JVal(xNew)
  225             self.__add_path(xNew, JNew)
  226             if self.__converged2(xNew - x, JNew - JVal, zeta ** 2):
  227                 self.__print_MSG(xNew, JNew, k + 1)
  228                 return xNew, JNew, True
  229
  230             gNew = self.__calc_grad(xNew)
  231             x, JVal, grad = xNew, JNew, gNew
  232         else:
  233             if self.__converged1(grad, zeta):
  234                 self.__print_MSG(x, JVal, maxIter)
  235                 return x, JVal, True
  236
  237         print("Adam not converged after {} steps!".format(maxIter))
  238         return x, JVal, False
  239
  240
  241     def get_path(self):
  242         return self.__xPath, self.__JPath
  243
  244
  245     def __converged1(self, grad, epsilon):
  246         if numpy.linalg.norm(grad, ord=numpy.inf) < epsilon:
  247             return True
  248         return False
  249
  250
  251     def __converged2(self, xDelta, JDelta, epsilon):
  252         val1 = numpy.linalg.norm(xDelta, ord=numpy.inf)
  253         val2 = numpy.abs(JDelta)
  254         if val1 < epsilon or val2 < epsilon:
  255             return True
  256         return False
  257
  258
  259     def __print_MSG(self, x, JVal, iterCnt):
  260         print("Iteration steps: {}".format(iterCnt))
  261         print("Solution:\n{}".format(x.flatten()))
  262         print("JVal: {}".format(JVal))
  263
  264
  265     def __calc_JVal(self, x):
  266         return self.__func(x)
  267
  268
  269     def __calc_grad(self, x):
  270         return self.__grad(x)
  271
  272
  273     def __init_x(self):
  274         return self.__seed
  275
  276
  277     def __init_path(self):
  278         self.__xPath.clear()
  279         self.__JPath.clear()
  280
  281
  282     def __add_path(self, x, JVal):
  283         self.__xPath.append(x)
  284         self.__JPath.append(JVal)
  285
  286
  287 class BPExPlot(object):
  288
  289     @staticmethod
  290     def plot_fig(adamObj):
  291         alpha = 0.001
  292         epoch = 50000
  293         x, JVal, tab = adamObj.get_solu(alpha=alpha, maxIter=epoch)
  294         xPath, JPath = adamObj.get_path()
  295
  296         fig = plt.figure(figsize=(6, 4))
  297         ax1 = fig.add_subplot(1, 1, 1)
  298
  299         ax1.plot(numpy.arange(len(JPath)), JPath, "k.", markersize=1)
  300         ax1.plot(0, JPath[0], "go", label="seed")
  301         ax1.plot(len(JPath)-1, JPath[-1], "r*", label="solution")
  302
  303         ax1.legend()
  304         ax1.set(xlabel="$epoch$", ylabel="$JVal$", title="solution-JVal = {:.5f}".format(JPath[-1]))
  305
  306         fig.tight_layout()
  307         # plt.show()
  308         fig.savefig("plot_fig.png", dpi=100)
  309
  310
  311
  312 if __name__ == "__main__":
  313     RGB, XYLv_ = getData(1000)
  314     bpObj = BPEx(RGB, XYLv_)
  315
  316     # rgb = (0.5, 0.6, 0.7)
  317     # xylv = bpObj.calc_xylv(rgb)
  318     # print(rgb)
  319     # print(xylv)
  320     # func = bpObj.calc_JVal
  321     # grad = bpObj.calc_grad
  322     # seed = bpObj.init_seed()
  323     # adamObj = Adam(func, grad, seed)
  324     # alpha = 0.1
  325     # epoch = 1000
  326     # adamObj.get_solu(alpha=alpha, maxIter=epoch)
  327     # xylv = bpObj.calc_xylv(rgb)
  328     # print(rgb)
  329     # print(xylv)
  330     # W0, W1 = bpObj.get_W0W1()
  331     # xylv = bpObj.calc_xylv(rgb, W0, W1)
  332     # print(rgb)
  333     # print(xylv)
  334
  335     func = bpObj.calc_JVal
  336     grad = bpObj.calc_grad
  337     seed = bpObj.init_seed()
  338     adamObj = Adam(func, grad, seed)
  339     BPExPlot.plot_fig(adamObj)

• 结果展示
  

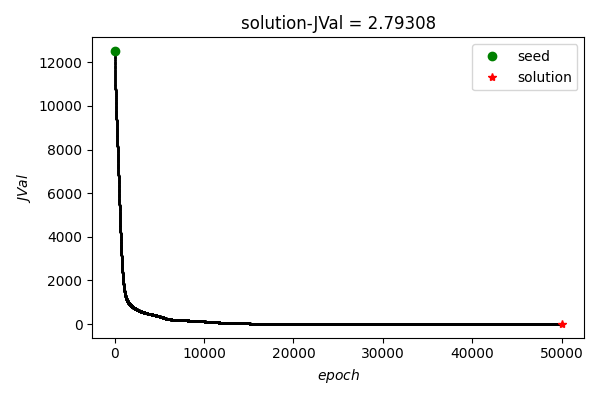
  可以看到, 在training data上总体loss随epoch增加逐渐降低.

• 使用建议
  ①. 某层之output节点可能受多个该层之input节点影响(如: softmax激活函数), 此时input节点具备source特性;
  ②. 正向计算过程可确定基础影响链路之梯度, 反向传播过程可串联基础影响链路之梯度;
  ③. 初值的选取对非凸问题的优化比较重要, 权重初值尽量不取全0.
• 参考文档
  ①. Rumelhart D E, Hinton G E, Williams R J. Learning internal representations by error propagation[R]. California Univ San Diego La Jolla Inst for Cognitive Science, 1985.
  ②. Adam (1) - Python实现