log 函数

什么是对数

对数用 log 符号来表示。根据底数的不同，log 可以变换成 lg、ln。lg 是以 10 为底的对数，ln 是以 e 为底的对数。

log_a^x=y，是一个以 a 为底，x 为真数的对数。条件：a > 0，且 a ≠ 1。根据底数的条件，对数的图像有两种：

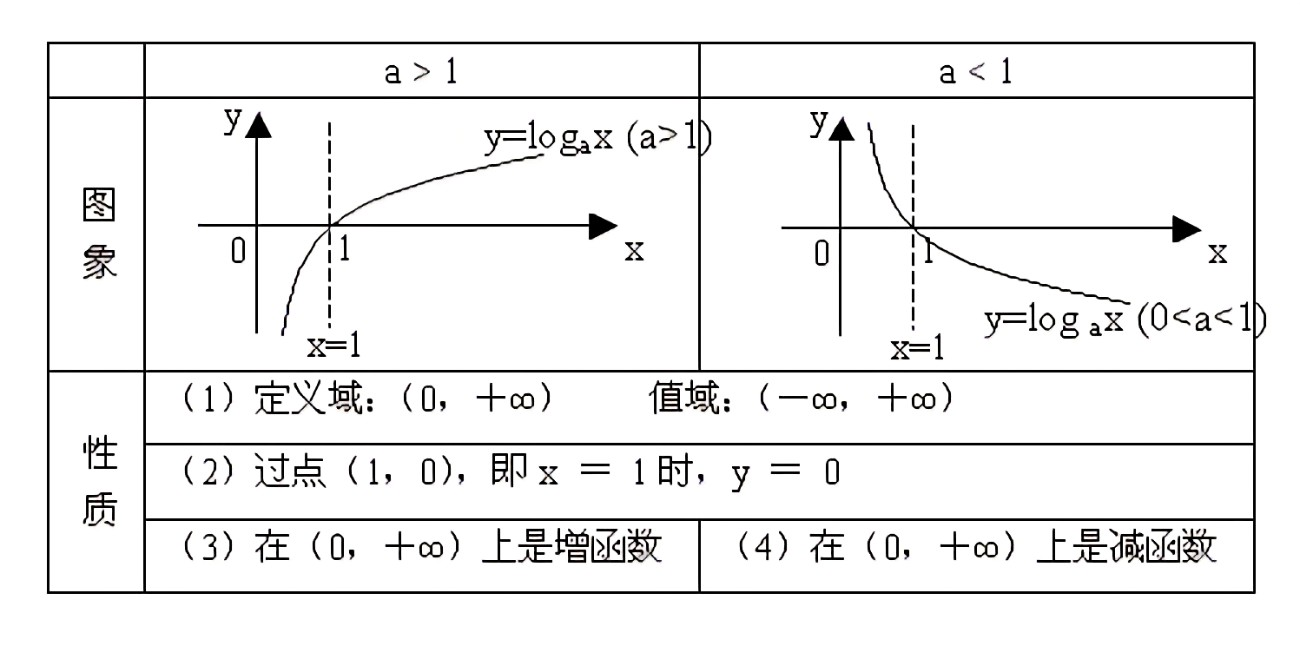
指数与对数可以互相转换，假如有一个对数：log₂⁸=3，指数 2³=8。底数还是指数的底数，指数中的次方就是对数中的结果，指数中的结果就是对数中的真数。

对数的公式

log_{a^M*N=loga^M+loga^N}

可以借助指数的公式来理解对数的公式。1️⃣令 x = log_a^M2️⃣令 y = log_a^N：

1. M = a^x
2. N = a^y

同底数幂相乘，底数不变，指数相加。所以，a^x+a^y = a^x*y=M*N：

\[M*N=a^{x*y}log{_a}^{M*N}=x*ylog{_a}^{M*N}=log{_a}^M+log{_b}^N
\]

把上面公式中第一步（指数）转换成对数，再把前面令的变量替换成相应的对数，最后得出的结果如本小节标题所示。log_a^M/N=log_a^M-log_a^N 的推导思路也类似上面，借助指数的公式来推。

log_a^Mn=nlog_a^M

假如，log₃²⁷ 可以写成 log₃³³，把 3 最高的那个 3 拿到 log 前面：3log_3³。而 log_3³ = 1，所以 3log_3³ = 3。

而 log₃²⁷ 就是 3 的多少次方等于 27，当然是 3³=27，即 log₃²⁷ = 3log_3³ = 3。

什么是换底公式

有一个对数 log_a^b，把 a 的底数换成 c，那么就有 log_c^b/log_c^a，这个过程就叫作换底。新的底数 c 可以是 10、5、e 等，具体的情况要根据题目要求来决定。换底公式在实际中非常常用，不是所有的对数的底数都是相同的，通过“换底公式”能够统一对数的底。

换底公式的运用

题目一

log_{5⁴ *} log_{5⁴ *} log_5⁴ * log_5⁴ = ?

这四个对数的底数都不一样，那么该选择哪个合适的底数来替换之前的底数呢？可以是 e，也可以是 10，不管选哪个都可以，目的是统一它们的底数从而继续计算下去。

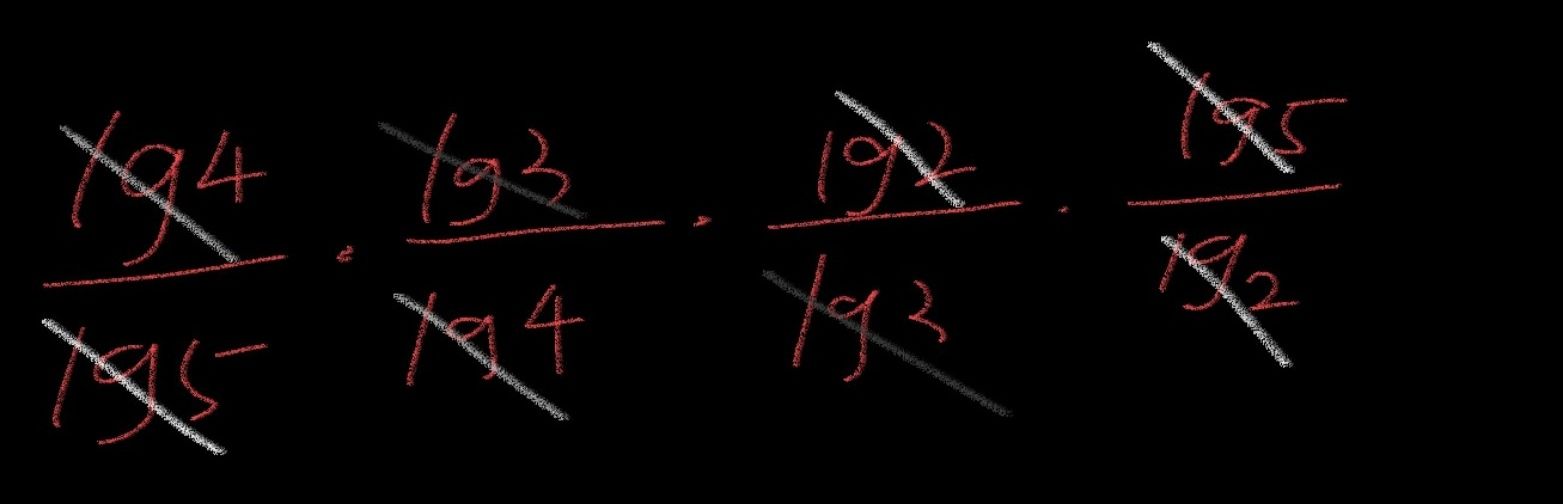
相同的分子和分母全部消掉之后的结果为 1。

题目二

已知 b > 0，log_5^b=a，lg^b=c，5^d=10，则下列等式一定成立的是（）？

A. d=ac B. a= cd C. c=ad D. d=a+c

题目中有对数也有指数，指数和对数可以互相转换^?。把 5^d=10 转换成对数：log₅¹⁰=d。现在，有两个对数的底数都是 5，应该把另一个对数的底数换成 5。

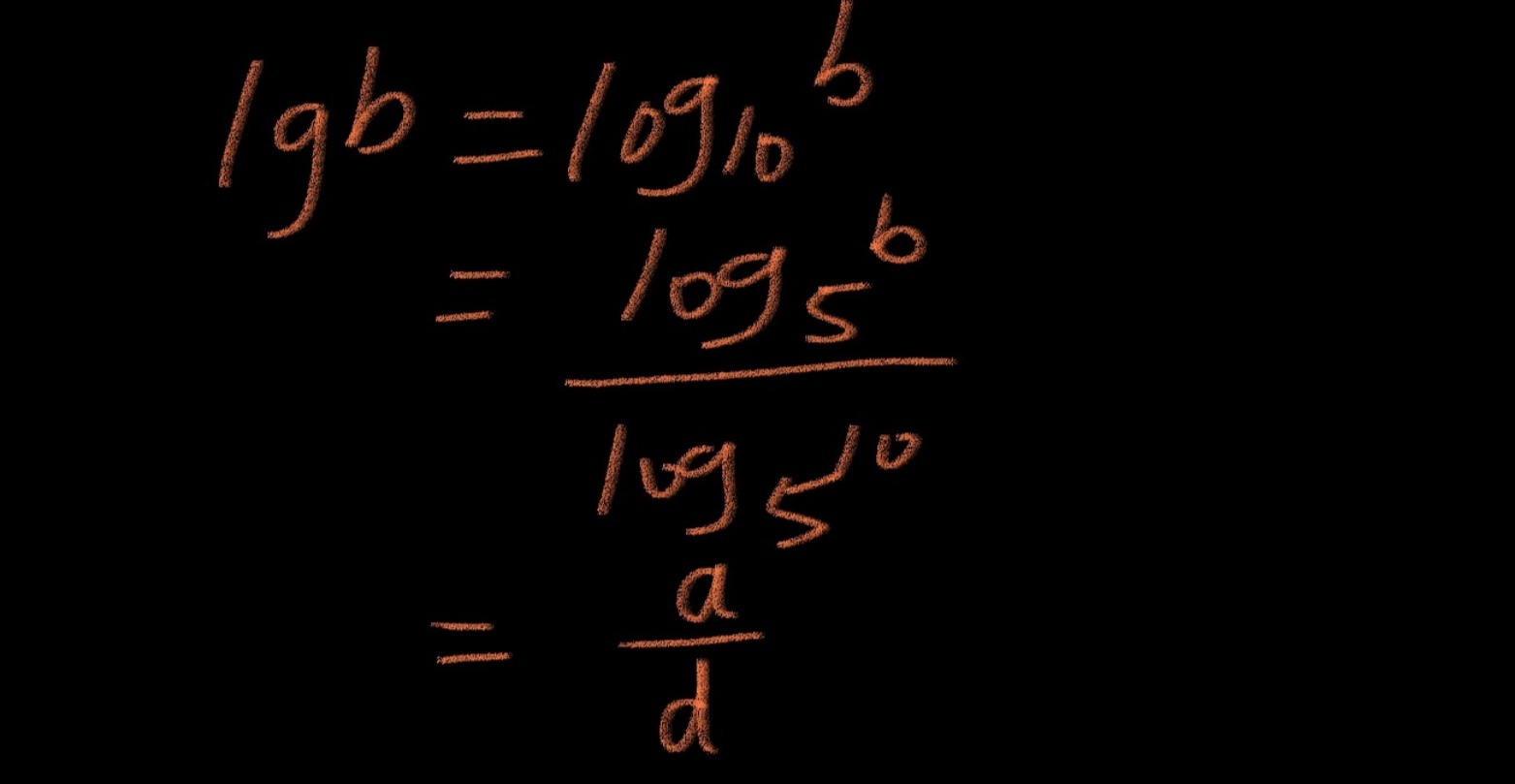
因为题目中已经告诉了我们 lg^b=c，最终计算出来的结果是选项 B。

换底公式的变式

明白了换底公式的过程之后，还有一个非常重要的变式在实际中也经常使用到：log_a^b = 1/log_b^a。下面是该变式的推导过程：

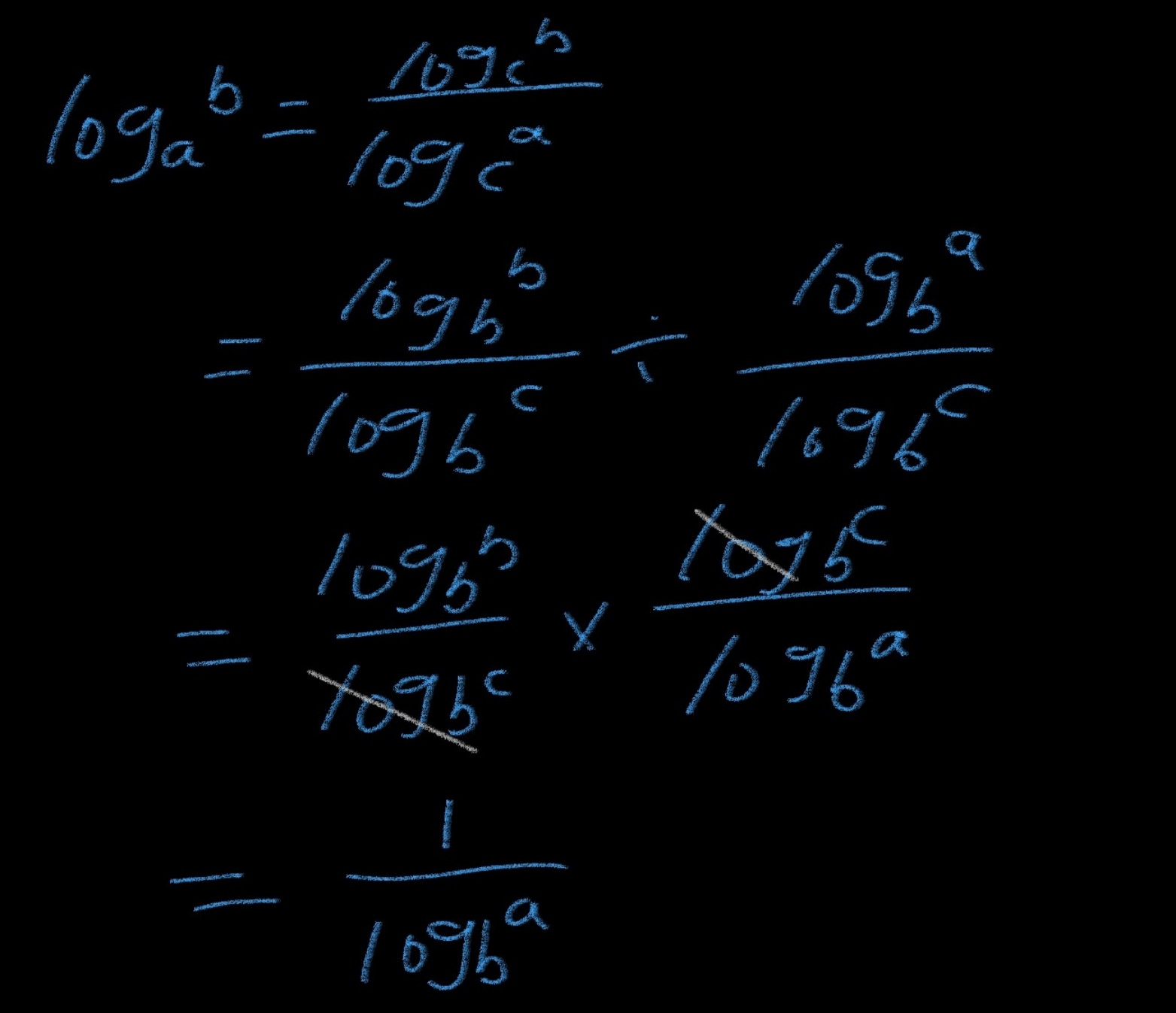
上面的计算过程中经历了两次换底过程。第一次换底中，把 log_a^b 的底 a 换成以 c 为底；第二次换底中，把所有对数的底换成以 b 为底。

结论：一个对数的底数与真数互换位置之后的倒数等于原本的对数。

题目一

求解：log₅^x-log_x²⁵=1

log_x²⁵ 可以写成 2log_x⁵。现在，我们来仔细观察前面的对数和这个对数，是不是底数与真数互换位置了？令 log₅^x 等于 t，2log_x⁵ 等于 2*1/t。

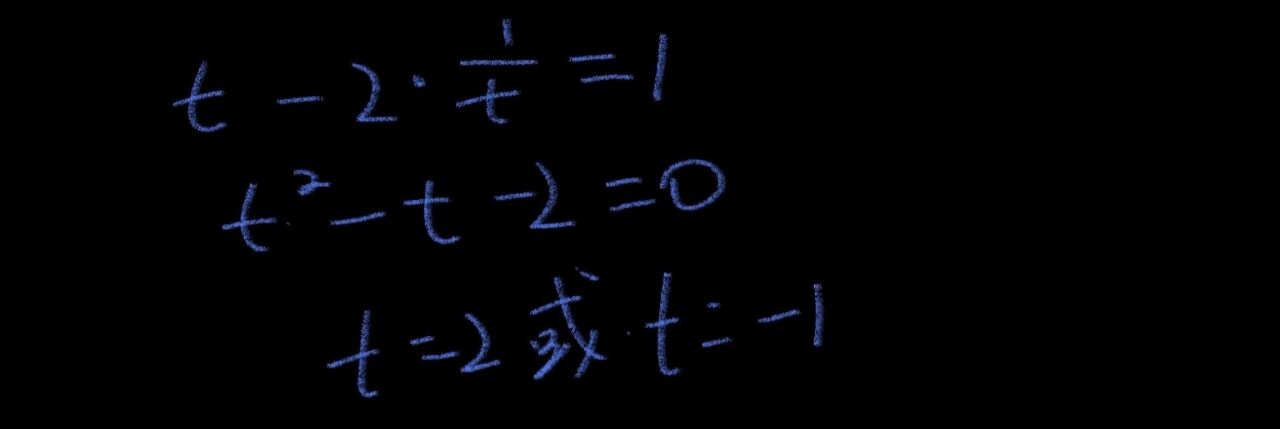
t = 2 或 t = -1，分两个情况：

• t = log₅^x = 2，把对数换成指数求得 x = 5² = 25；
• t = log₅^x = -1，对数换成指数求得 x = 5^-1 = 1/5。

为什么令“2log_x⁵ 等于 2*1/t”？

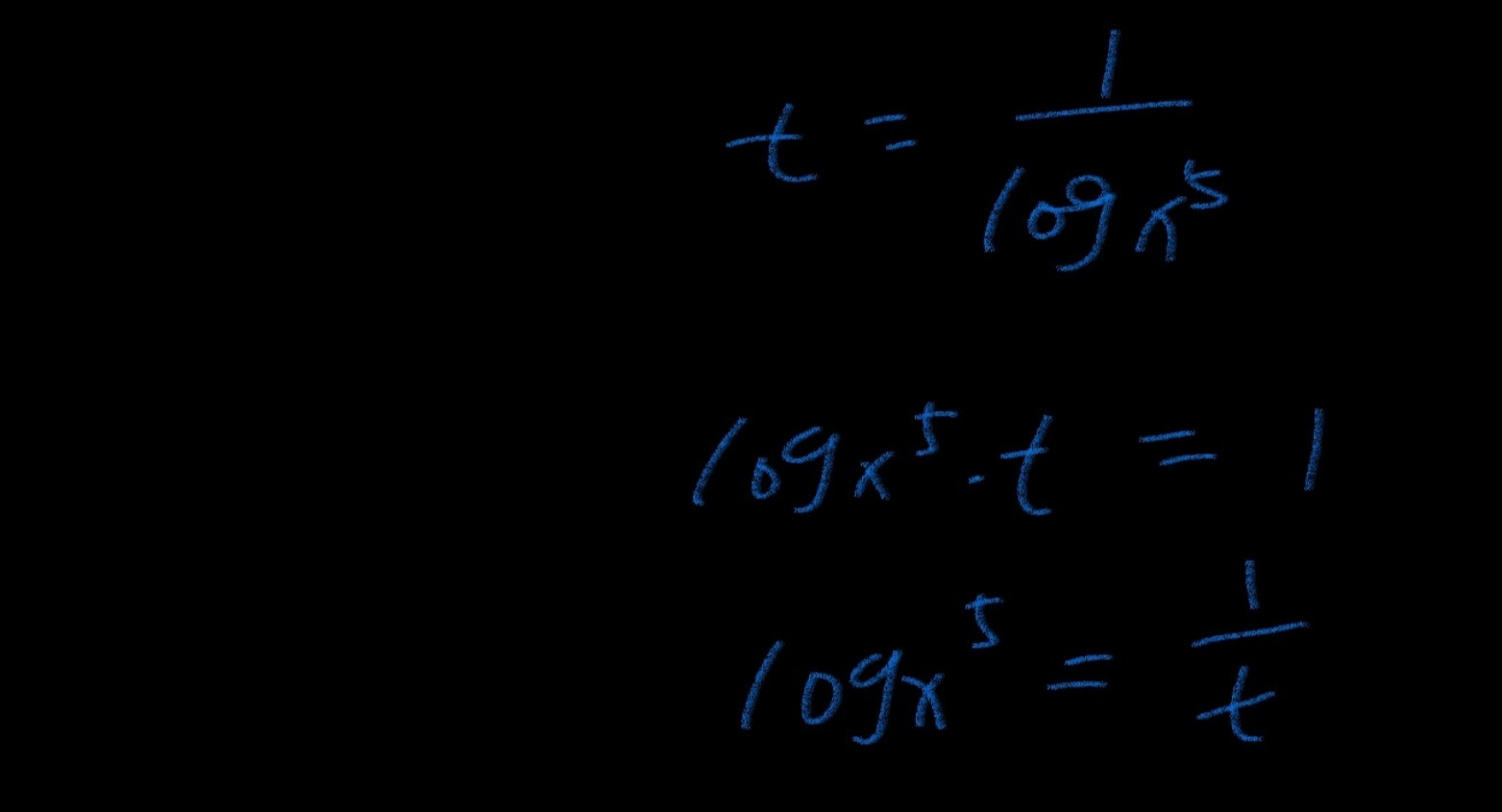
因为 log₅^x = t，由换底公式变式可知，所以，t = 1/log_x⁵，即 log_x⁵ = 1/t。注意：这里为了讲解，忽略了 log_x⁵ 前面比较挡视野的 2。